Файл: Сборник задач по технологии и технике нефтедобычи Учеб, пособие для ву.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 387
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
и относительной шероховатости трубы s/D по диаграмме (см. рис. 5.3) или по (5.22).
Пробковая структура. Модель потока дрейфа Уоллиса [27] и уточнения, внесенные в нее Оркишевским на основе результатов исследования влияния вязкости жидкости на ха-
120
| и 3 s | п | ^1 | а2 | “з | О 4 | а5 | Предельные значения параметра |
| Жидкая фаза — вода | | | | | |||
| <3 | 1,38 | 0,0025 | 0,232 | —0,428 | —0,7821 | — | К ^ —0,213*&усм |
| >3 | 0,799 | 0,0174 | —0,162 | —0,888 | — 1,2508 | — | ^ ^ WS (1 Рсм/рж) WCM + ws |
| Жидкая фаза — нефть <3 | 1,415 | 0,0024 | 0,167 | 0,113 | —0,1395 | — | К> -0,213-ауСм |
| >3 | 1,371 | 0,0054 | | 0,569 | 0,455 | * | у — Ws 0 рсм/рж) |
| | | | | | | Wck + Ws |
• а. = -(0.516 4 lg а>см) [0.0015 lg (цж + 1)/0[,571 + 0,63 lg £>т 4 0,722].
Относительная скорость движения газовых пузырей (пробок)
определяется следующим образом:
1 ... 37 38 39 40 41 42 43 44 ... 93
ws=c1c2YgDT’ м/с, (5.63)
где <4 — коэффициент для случая движения газовой пробки в не-
подвижной жидкости и являющийся функцией числа Рейнольдса
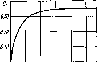
пробки (рис. 5.9)
? Ren = wsDT ржфж.
(5.64
121
о 10 20 JO 00 50Щ
Рис. 5.9. График зависимости Сг от Ren [ 19 ]
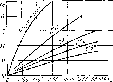
Рис. 5.10. График зависимости С2 от Re>K и Ren [19]
с2 — коэффициент для случая движения газовой пробки в движущейся жидкости и являющийся функцией числа Рейнольдса пробки и числа Рейнольдса жидкости при скорости движения ее, равной скорости смеси (рис. 5.10) wx — wCM
Rc>k — ^смРтРж/Цж. (5.65)
Приведенные зависимости для коэффициентов с1 и с2 позволяют рассчитать ws итерационным методом. Для полностью развитой пробковой структуры можно принять с1 = 0,35.
Если число Рейнольдса жидкости больше предельного значения, т. е. Реж>6000, то ws можно определить методом экстраполяции с использованием уравнений:
если Rensg;3000, то
=70,546 + 8>74-10-6Re»)VAgDT - м/с- (5-66)
если 3000 < Ren < 8000, то сначала определяется ais0 = (0,251 + 8,74-Ю-6 Re*) м/с’ а затем (5.67)
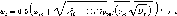
если wn ^ 8000, то
ws = (0,35 + 8,74-10
6
Re*) VgDr . м/с’ (5.69)
где рж — мПа-с; рж — кг/м3; Dr — м.
Плотность газожидкостной смеси рсм определяют по (5.39), а градиент потерь на трение по уравнению для однофазного потока, движущегося со скоростью, равной приведенной скорости смеси
(dp/dH)TV = XwltilpculQ-6l(9Dr), МПа/м, (5.70)
где Я — коэффициент гидравлического сопротивления потока жидкости, движущейся со скоростью wx = wCM, определяется в зависимости от числа Re* и относительной шероховатости e/DT по диаграмме (см. рис. 5.3) или по (5.22).
122
Переходная структура. Определение плотности смеси и градиента потерь на трение ориентировочно определяют по формулам средневзвешенного распределения [19]
Рем = (^гб п — ^гб) Рем пр/С^гб п а>гб с)-Ь(и>гб—ОУгб с) ‘ Рем к/(^гб п—^гб с)*
(5.71)
пр/(дагб п — ^гб с) + («»гб — о>Гб с) X
X
где рем пр; Рем к — соответственно плотности смеси пробковой и кольцевой структур потока; (dP/dH)rp пр; (dp/dH)rpK — соответственно градиенты потерь на трение пробковой и кольцевой структур потока.
Кольцевая структура. Ввиду непрерывности и больших скоростей газовой фазы, поток которой содержит диспергированные капли жидкости, допускается, что относительная скорость пренебрежимо мала (ws -*• 0), в силу чего плотность смеси определяется по формуле
Рем = Рж (1 Рг) + РгРгч (5.73)
градиент потерь на трение — по уравнению для однофазного потока
где шг пр — приведенная скорость газа, м/с; К — коэффициент гидравлического сопротивления потока газа, определяющийся в зависимости от числа Рейнольдса для потока газа
Rep — и/p пР^тРг/^г‘ (5.75^
и относительной шероховатости (волнистости) пленки жидкости на стенке трубы e/DT по диаграмме (см. рис. 5.3) или по (5.22).

