Добавлен: 20.03.2024
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Заключение
О математических софизмах можно говорить бесконечно много, как и о математике в целом. Софизмы - это смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Буквально вспомнив, кто же такие были софисты, можно понять, что основной задачей было постижение философии. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.
Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми.
Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика-это целая наука, а именно математические софизмы - это лишь часть одного большого течения.
Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научится искать ошибки в рассуждениях других людей, научится 18 грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку.
И в конце хотелось бы сказать, что все мои цели, поставленные мной в начале работы, были мной достигнуты.
Источники
-
https://infourok.ru/issledovatelskaya_rabota_sofizmy_i_paradoksy-485868.htm -
«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003. -
«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961. -
«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971. -
«Парадоксы науки». Автор: А.К.Сухотин. Издательство "Молодая гвардия", 1978 г. -
https://infourok.ru/issledovatelskaya-rabota-po-matematike-na-temu-matematicheskie-sofizmi-i-paradoksi-1986353.html -
Шамина, В. В. Математические парадоксы и софизмы / В. В. Шамина, В. Е. Матешин, А. А. Ефремова, О. В. Шмелева. — Текст: непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 47-50. — URL: https://moluch.ru/young/archive/9/639/ -
https://habr.com/ru/post/197578/
Приложение
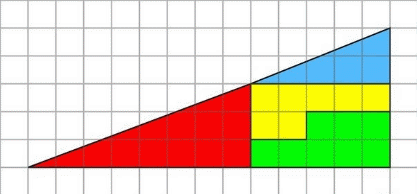
Рис. 1
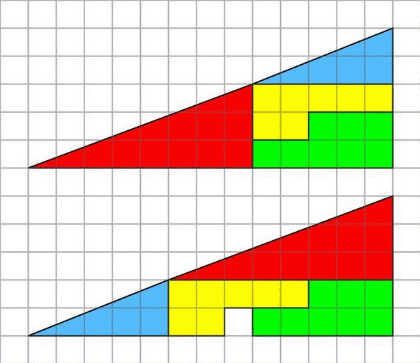
Рис. 2

Рис. 3
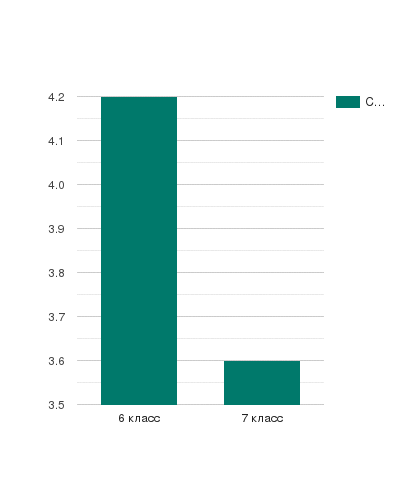
Диаграмма 1
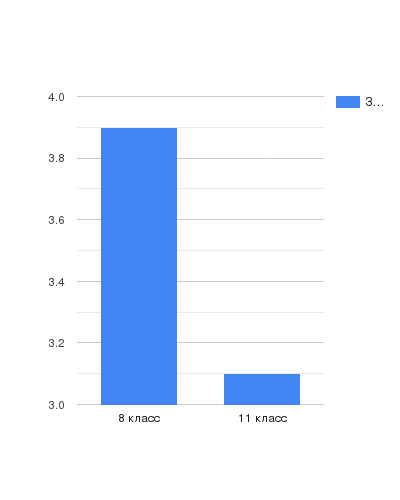
Диаграмма 2

