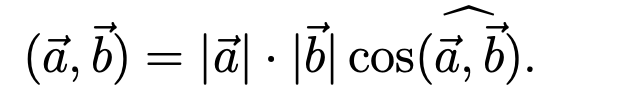1. 
   Матрицы и линейные действия над ними. Определение матрицы. Размерность. Прямоугольная, квадратная, матрица столбец и строка, диагональная и единичная. Транспонирование матрицы.
   

Матрицей размера m × n называется совокуп- ность m · n элементов некоторого множества, записанных в виде прямоугольной таблицы, содержащей m строк и n столбцов.

m × n : Размерность у матрицы

если количество строк в матрице равно количеству столбцов (m = n), то матрица называется квадратной порядка n

Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Квадратная матрица, на главной диагонали которой стоят какие-то числа λ₁, λ₂, . . ., λ_n, а все остальные элементы матрицы – нули, называется диагональной.

иагональная матрица, все диагональные элементы которой равны 1, называется единичной.

Пусть A – матрица размера m × n. Матрица размера n × m, столбцы которой совпадают с соответствующими строками матрицы A, называется транспонированной к матрице A и обозначается A^T .

Заметим, что строки матрицы A^T совпадают с соответствующими столбцами матрицы A.

Транспонированную матрицу обозначают также A^t или A^′.

2. 
   Сумма матриц и ее свойства. Произведение матрицы на число, его коммутативность, ассоциативность и дистрибутивность.
   

- Операция сложения определена только для матриц одинакового раз-

мера.

Суммой матриц A и B одинакового размера
m × n называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц A и B

A+B=C (C –матрицаразмераm×n), приэтом.

Если A – матрица размера m × n, α – число,

то :αA = B (B – матрица размера m × n), при этом

1. 
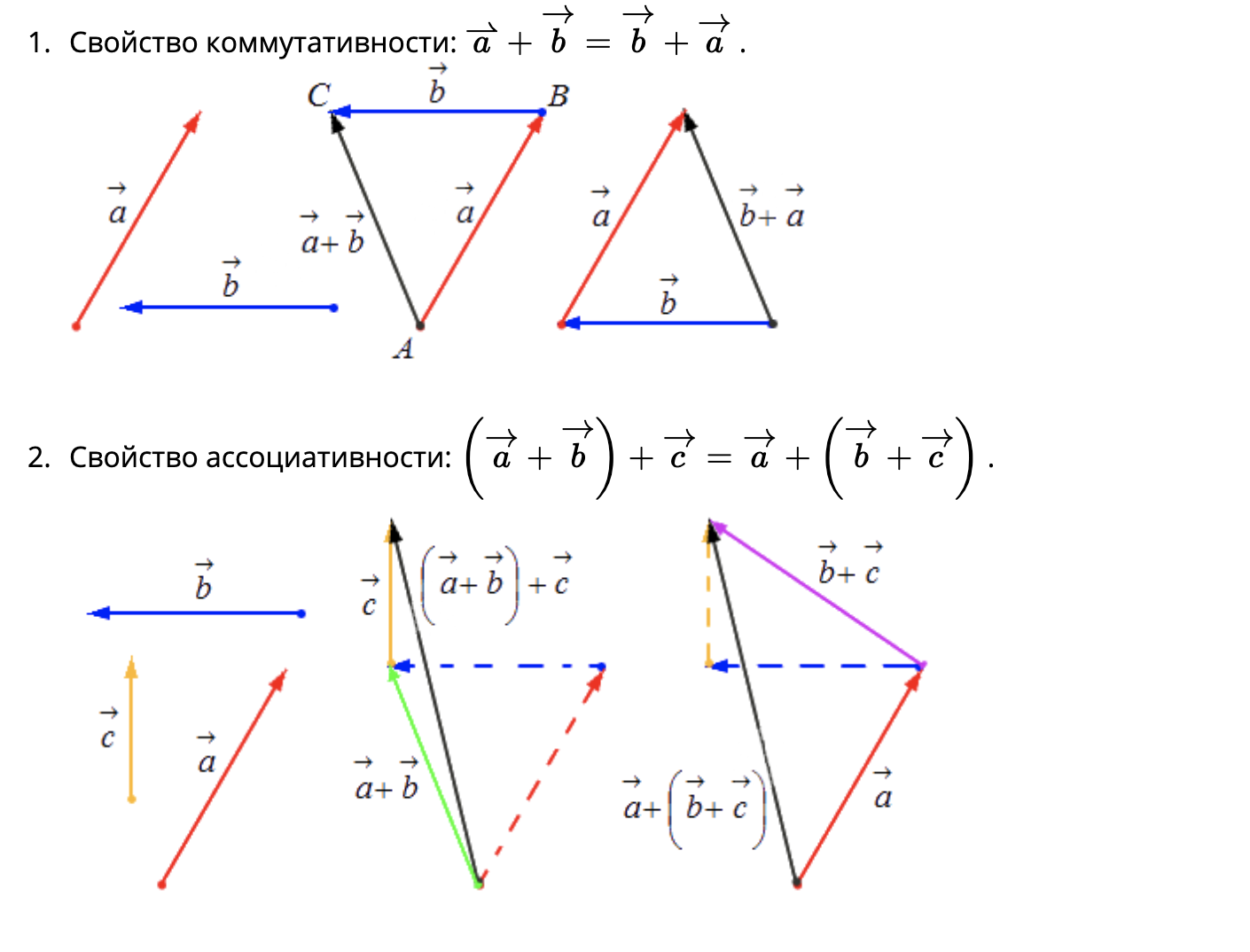
   A+B=B+A; (Коммутативность)
   
2. 
   (A+B)+C=A+(B+C); (Ассоциативность)
   
3. 
   (αβ)A = α(βA); (ассоциативность)
   
4. 
   (α+β)A=αA+βA; (дистрибутивность)
   
5. 
   α(A+B)=αA+αB, (дистрибутивность)
   

где A, B, C – матрицы одинакового размера, α, β – числа.

3. 
   Произведение матриц. Определение. Свойства. Умножение на единичную матрицу.
   

- Произведением матрицы A размера m × n на матрицу B размера n × k называется матрица C размера m × k (AB = C).

Некоторые свойства операции умножения:

1. (AB)C = A(BC);
2. (A+B)C=AC+BC, C(A+B)=CA+CB; 3. α(AB) = (αA)B = A(αB);

---

4. (AB)^T=B^TA^T;
5. (AB)^∗ = B^∗A^∗,
где A, B, C – матрицы, α, β – числа.

Нетрудно заметить, что если A – квадратная матрица произвольного

порядка, I – единичная матрица того же порядка, то также справедливы равенства AI = IA = A.

4. 
   Определение квадратной матрицы. Понятие определителя. Минор. Алгебраическое дополнение. Разложение определителя по элементам строки или столбца. Транспонирование матрицы.
   

- Каждой квадратной матрице A ставится в соответствие число, которое называется определителем или детерминантом и обозначается det A.

-Число M_ij, равное определителю полученной матрицы, называется дополнительным минором или минором элемента a_ij матрицы A.

-Число A_ij = (−1)^i+jM_ij называется алгебраическим дополнением элемента a_ij матрицы A.

- Определитель матрицы не изменится, если его разложить по любой строке или любому столбцу матрицы.

Разложение определителя по i-й строке: detA=a_i1A_i1+a_i2A_i2+...+a_inA_in =

= a_i1(−1)ⁱ⁺¹M_i1 + a_i2(−1)ⁱ⁺²M_i2 + . . . + a_in(−1)ⁱ⁺ⁿM_in. Разложение определителя по j-му столбцу:

detA=a_1jA_1j +a_2jA_2j +...+a_njA_nj = =a_1j(−1)^1+jM_1j +a_2j(−1)^2+jM_2j +...+a_nj(−1)^n+jM_nj.

Разложение определителя удобно выполнять по той строке (столбцу), в которой находится наибольшее количество нулей.

Для любой квадратной матрицы A: detA^T =detA.

5. 
   Свойства определителей. Замена строк и столбцов определителя. Определители с одинаковыми строками, столбцами. Общий множитель строки. Нулевые и линейно зависимые строки, столбцы.
   

- Если в матрице поменять местами 2 столбца, то определитель матрицы меняет знак (умножается на (−1)):

detA₁ ...A_j ...A_k ...A_n = −detA₁ ...A_k ...A_j ...A_n.

-Определитель матрицы равен нулю, если в матрице – 2 пропорциональных (tỉ lệ) столбца:

det [A₁ . . . B . . . λB . . . A_n] = 0.

В частности, если в матрице – 2 одинаковых столбца (строк), то ее определи- тель равен нулю.

- Если в матрице какой-то столбец умножить на число, то опре-

делитель матрицы умножается на это число:

---

Это свойство можно сформулировать иначе.

Если элементы какого-то столбца матрицы имеют общий множи- тель, то его можно вынести за знак определителя.

- Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.

- Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.

6. 
   Свойства определителей. Определитель как сумма определителей. Тождественное преобразование определителя. Сумма произведений элементов строк и столбцов на алг. дополнения других строк, столбцов.
   

-Определитель матрицы не изменится, если какой-то ее столбец

умножить на число и сложить с другим столбцом этой матрицы:

det(A₁ ...A_j ...A_k ...A_n) = detA₁ ...(A_j + λA_k)...A_k ...A_n. ) (Тождественное преобразование определителя)



(*)

7. 
   Система линейных уравнений в матричной форме и ее решение с помощью обратной матрицы.
   

- AX = B.
Это означает, что систему линейных уравнений можно записать как

одно матричное уравнение

Если A – невырожденная квадратная матрица, то решением матрич- ного уравнения AX = B является матрица X = A⁻¹B, а решением мат- ричного уравнения XA = B – матрица X = BA⁻¹.

8. 
   Системы линейных алгебраических уравнений с квадратной матрицей. Формулы Крамера.
   

Теорема 3.1. (Крамера) Система линейных алгебраических уравне- ний (3.1) с квадратной матрицей A имеет единственное решение тогда и только тогда, когда det A ̸= 0 (матрица системы – невырожденная).

Метод крамера: sgk -42

9. 
   Существование и единственность решения однородной системы линейных уравнений.
   

- Однородная система линейных уравнений всегда имеет нулевое реше- ние: x₁ = 0, x₂ = 0, . . . , x_n = 0, поэтому такая система всегда совместна.

Теорема 3.2. Однородная система линейных уравнений с квадратной матрицей системы A (m = n) имеет единственное (нулевое) решение тогда и только тогда, когда матрица системы невырожденная (det A ̸= 0).

---

Теорема 3.3. Если в однородной системе линейных уравнений число уравнений меньше числа неизвестных (m < n), то такая система имеет бесконечно много решений.

10. 
    Существование и единственность решения неоднородной системы линейных уравнений ???????????/
    
11. 
    Определение вектора. Обозначение. Коллинеарность. Модуль. Равенство векторов
    

Векторы ⃗a и ^⃗b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, в противном случае векторы назы-

ваются неколлинеарными.

Длину вектора: Модуль

Векторы называются равными, если они сонаправлены и их длины равны

12. 
    Линейные действия над векторами. Сумма векторов и ее свойства. Нулевой вектор. Противоположный вектор. Разность векторов. Произведение вектора на число и его свойства.
    

• 
  Описанную схему сложения нескольких векторов называют также правилом многоугольника . 
  

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху. 

Противоположно направленные векторы – это коллинеарные векторы, направленные в противоположные стороны.
вычитание векторов (разность векторов) a - b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:

с_i = a_i - b_i

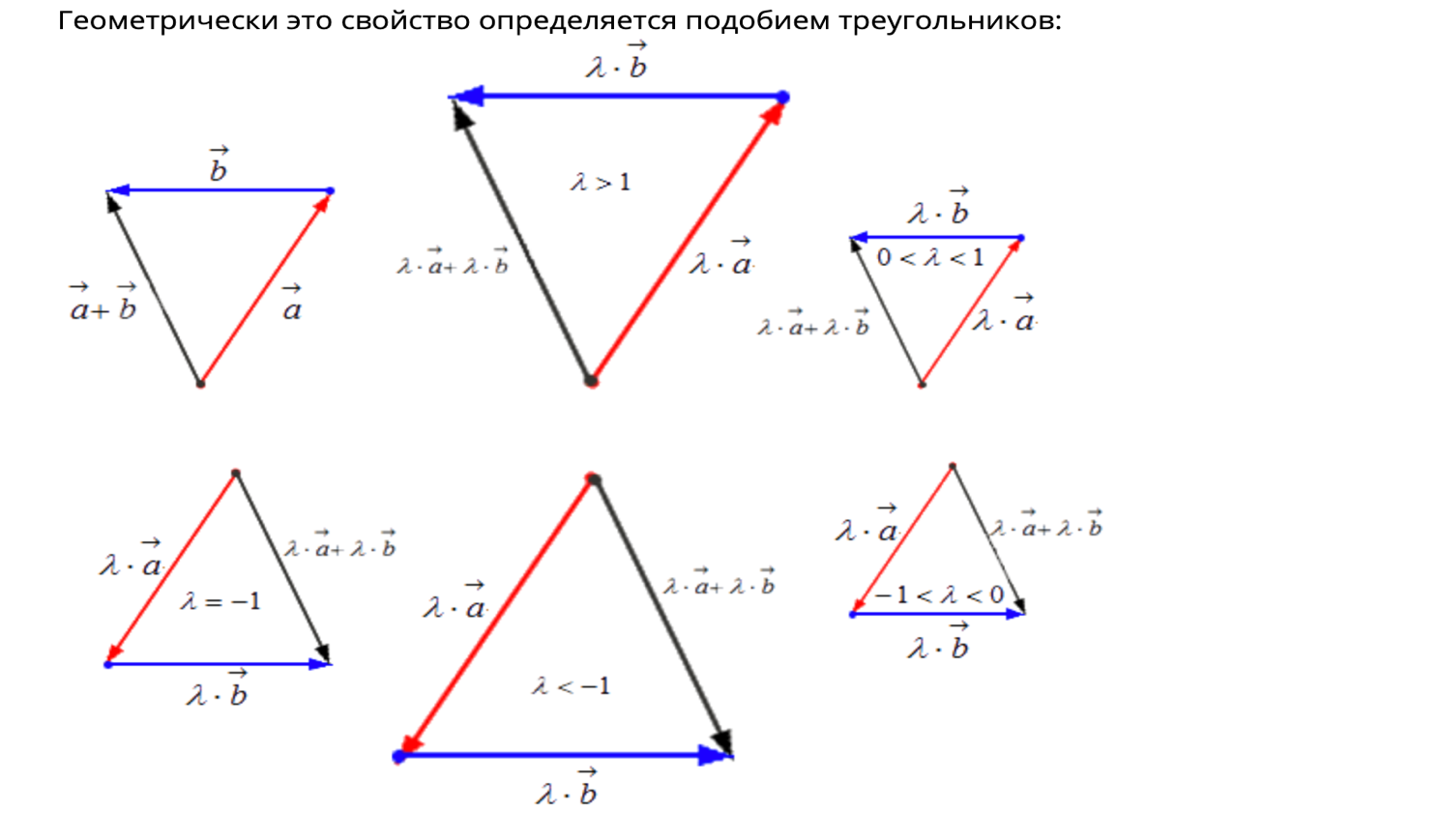
Произведением ненулевого вектора  на действительное число называется вектор , удовлетворяющий условиям:

1) длина вектора  равна

---

, т.е. ;

2) векторы  и коллинеарные ;

3) векторы  и одинаково направлены, если , и противоположно направлены, если . (рис. 9). Если среди сомножителей  есть 0, то под произведением понимается нулевой вектор.

13. 
    Проекция вектора на вектор, геометрический смысл. Свойство линейности
    

Проекцией  вектора на направление вектора , называется число, которое равно величине проекции вектора   на ось  , проходящую через второй вектор   (рис. 2).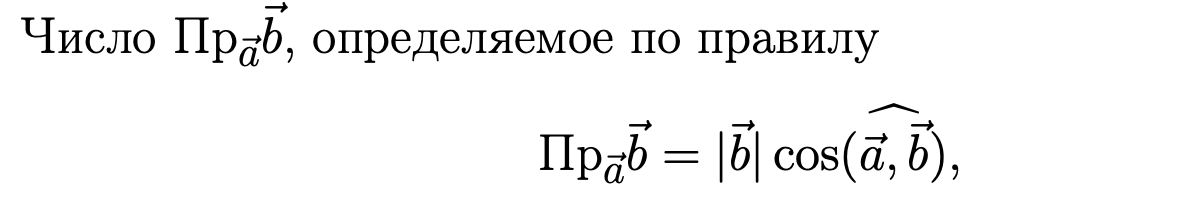

Проекция вектора на вектор представляет собой отрезок на векторе, полученный перпендикулярами, опущенными из начала и конца вектора либо на сам вектор, либо на его продолжение

14. 
    Скалярное произведение векторов и его свойства. Связь с проекцией вектора на вектор. Перпендикулярность векторов. Орт вектора. Связь вектора со своим ортом.
    

- Скалярным произведением (⃗a,^⃗b) векторов ⃗a, ^⃗b ∈ R³ называется вещественное число, равное произведению длин векторов на косинус угла между ними:

---

Смотрите также файлы

• Федеральное агентство по образованию Федеральное государственное образовательное учреждение Высшего профессионального образования Российский государственный университет туризма и сервиса.docx

• Респираторлы ауру Жедел респираторлы аурулар полиэтиологиялы аурулар тобына жатады.pptx

• Оцените характер стратегического поведения на рынке какойлибо организации с точки зрения динамики ее поведения и дайте обоснование своей оценки.docx

• Задача 1 Определите верную стратегию выхода из психологической игры и разрешения конфликтной ситуации. Помните о том, что вы находитесь в роли руководителя. Сейчас я тебе покажу.docx

• Итоговый тест, по истории Нижегородского края. 8 класс с какими целями ПетрI посещал н новгород в 1695 году.docx