Ортом или единичным вектором   называется вектор, модуль которого равен единице.

(о связи между вектором и его ортом). Всякий ненулевой вектор может быть представлен в виде произведения модуля этого вектора на его орт:

15. 
    Разложение вектора в декартовом базисе. Декартова система координат и декартов базис. Равенство векторов в декартовом базисе. Геометрический смысл компонентов.
    

-теорема. Любой вектор  , заданный в пространстве0xyz, может быть представлен в виде

. (3.4)

Такое представление вектора  называется разложением вектора в декартовом базисе или разложением вектора по ортам.

- Векторы  единичные векторы осейОx, Oy, Oz

- Поскольку  некомпланарны, то они образуют базис в пространстве, который называют декартовым базисом.

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости.

Одна из осей называется осью Ox, или осью абсцисс, другая – осью Oy, или осью ординат. Эти оси называют также координатными осями.

Обозначим через M_x и M_y соответственно проекции произвольной точки M плоскости на оси Ox и Oy.


-Базис на плоскости и в пространстве называется декартовым, если он состоит из единичных взаимно перпендикулярных векторов.

16. 
    Действия над векторами в декартовом базисе. Сложение, вычитание, умножение на скаляр. Скалярное произведение ???????/hỏi lại??
    
17. 
    Направляющие косинусы векторов. Угол между векторами. Условие параллельности и перпендикулярности. Расстояние между данными точками.
    

---

-

Из определения скалярного произведения следует правило нахожде- ния косинуса угла между векторами:



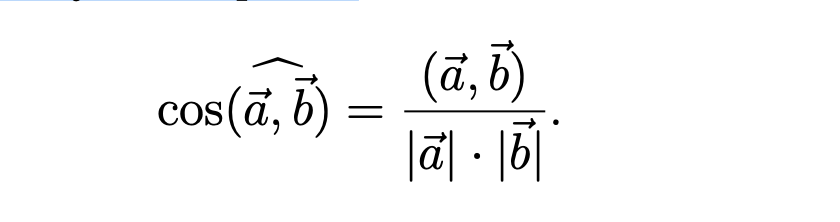
Зная cos(⃗a,^⃗b), можно найти угол между векторами ⃗a и ^⃗b.

-векторы перпендикулярны, то угол между ними равен 90º

-Угол между параллельными векторами 0° или 180

18. 
    Векторное произведение. Представление в виде определителя. Свойства антикоммутативности, ассоциативности, дистрибутивности. Ориентация результирующего вектора. Модуль векторного произведения, его геом. смысл.
    

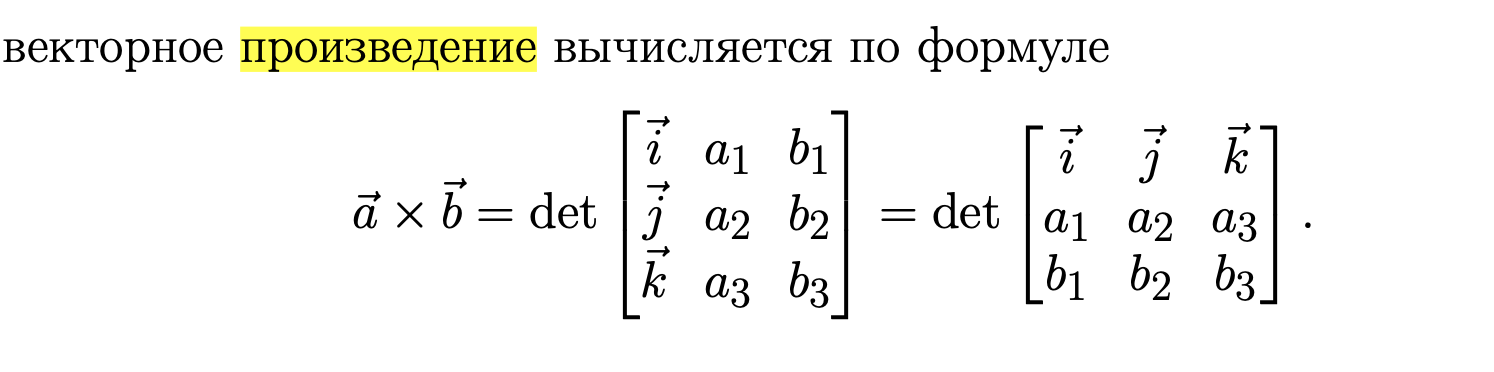
Свойства векторного произведения векторов:

1. 
   ⃗a × ^⃗b = −(^⃗b × ⃗a). (антикоммутативности)
   
2. 
   (λ⃗a) ×^⃗b = ⃗a × (λ^⃗b) = λ(⃗a ×^⃗b) для любого числа λ. (ассоциативности)
   
3. 
   (⃗a + ^⃗b) × ⃗c = ⃗a × ⃗c + ^⃗b × ⃗c и ⃗a × (^⃗b + ⃗c) = ⃗a × ^⃗b + ⃗a × ⃗c , (дистрибутивности)
   

где ⃗a,^⃗b,⃗c ∈ R³.

Модуль векторного произведения:

Длина вектора, являющегося векторным произведением векторов ⃗a и ^⃗b, численно равна площади параллелограмма, построенного на этих векторах

19. 
    Смешанное произведение векторов. Определение, представление в виде определителя. Геометрический смысл. Условие компланарности трех векторов.
    

- Смешанным произведением векторов ⃗a,^⃗b,⃗c ∈ R³ называется число, равное скалярному произведению вектора ⃗a на векторное произведение векторов ^⃗b и ⃗c:

( (⃗a,^⃗b × ⃗c).
Смешанное произведение векторов (⃗a,^⃗b×⃗c) обозначают также⃗a·^⃗b·⃗c.



- модуль смешанного произведения векторов ⃗a, ^⃗b, ⃗c равен объему V парал- лелепипеда, построенного на этих векторах

- Три вектора ⃗a,^⃗b,⃗c компланарны тогда и только тогда, когда (⃗a,^⃗b × ⃗c) = 0.

---

20. 
    Прямая на плоскости в декартовых координатах. Формы уравнения прямой. Угол между прямыми, перпендикулярность. Параллельность. Расстояние от точки до прямой.
    

- Любая прямая, лежащая в плоскости, задается уравнением

Ax + By + C = 0,

где A и B одновременно не обращаются в ноль, которое называется общим уравнением прямой.

21. 
    Плоскость в декартовых координатах. Общее уравнение плоскости. Уравнения плоскости, проходящей через три точки. Расстояние от точки до плоскости.
    

22. 
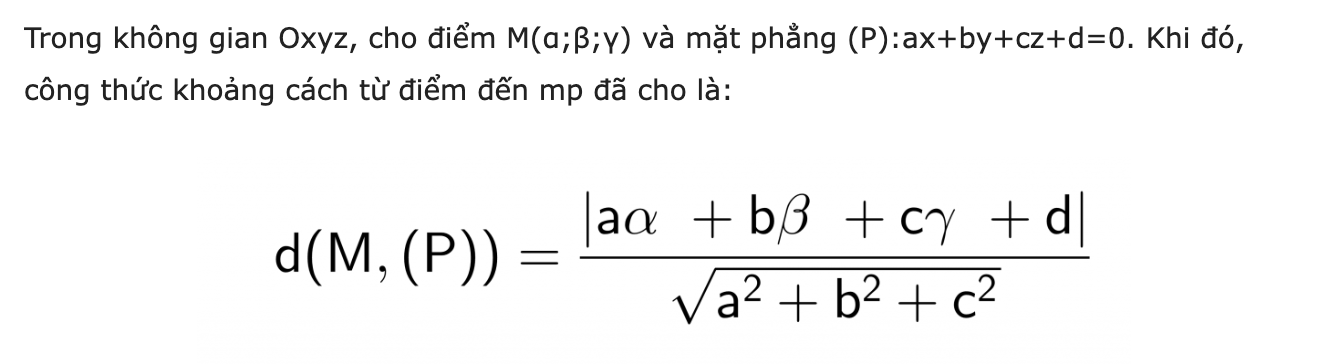
    Прямая в декартовых координатах. Канонические уравнения прямой. Уравнение прямой по двум точкам. Параметрические уравнения.
    

23. 
    Условие принадлежности 2-х прямых одной плоскости. Угол между прямой и плоскостью. Условие перпендикулярности и параллельности.
    

- Прямые лежат в одной плоскости. если они 1) пересекаются;2) параллельны.




26. Собственные числа и собственные векторы самосопряженной матрицы. Ортогональность собственных векторов. Приведение матрицы к диагональному виду. (sgk-56)

27. Кривые второго порядка. Общее уравнение линий второго порядка

28.Окружность, эллипс, гипербола, парабола.

29.Приведение общего уравнения кривой второго порядка к каноническому виду

30.Поверхности второго порядка

---

Смотрите также файлы

• Федеральное агентство по образованию Федеральное государственное образовательное учреждение Высшего профессионального образования Российский государственный университет туризма и сервиса.docx

• Респираторлы ауру Жедел респираторлы аурулар полиэтиологиялы аурулар тобына жатады.pptx

• Оцените характер стратегического поведения на рынке какойлибо организации с точки зрения динамики ее поведения и дайте обоснование своей оценки.docx

• Задача 1 Определите верную стратегию выхода из психологической игры и разрешения конфликтной ситуации. Помните о том, что вы находитесь в роли руководителя. Сейчас я тебе покажу.docx

• Итоговый тест, по истории Нижегородского края. 8 класс с какими целями ПетрI посещал н новгород в 1695 году.docx