Поставщики и их мощности, тыс.куб. м.		Потребители и их спрос, тыс.куб.м.
		B1	B2	B3		B4
		250	300	400		300
A1	250	7 250	6	4	5
A2	400	5	7 300	4 100	7
A3	150	9	8	9 150	4
A4	150	4	3	3 150	9
A5	300	6	5	6	8 300

В итоге получили некоторое возможное решение. Проверка сумм ∑Xij по строкам и столбцам показывает на допустимость такого плана распределения поставок и отсутствие арифметических ошибок.

Вычислим значение целевой функции. Для этого перемножим удельные стоимости доставки на соответствующие объемы и найдем сумму




=7*250+7*300+4*100+9*150+3*150+8*300=8450 тыч. руб.

Рассмотрим еще один способ составления начального плана - способ минимального элемента. Способ минимального элемента несколько сложнее, но позволяет отыскать начальное решение очень близкое к оптимальному, а иногда и оптимальное.

Сущность его заключается в следующем. В матрице стоимостей отыскивается клетка с минимальным значением C_ij и в эту клетку записывается поставка X_ij=min (a_ib_i). Если матрица содержит несколько одинаковых минимальных значений C_ij, то выбирают любое одно. После этого вычеркивается строка или столбец. Если a_{i ˃} b_i, вычеркивают столбец, при a_i<b_iвычеркивают строку. Далее процесс (итерации, шаги) повторяют до тех пор

---

, пока не будут распределены все поставки.

Если матрица большая и в уме не удержать нераспределенные мощности и спрос на шагах в процессе распределения на части значений a_i и b_j, в конце каждого шага остаточные величины записывают.

Рабочая таблица имеет форму, приведенную в таблице 3.

Таблице 3

Построение опорного плана по методу минимального элемента.

Поставщики и их мощности, тыс.куб. м.		Потребители и их спрос, тыс.куб.м.
		B1	B2	B3		B4
		250	300	400		300
A1	250	7 100	6	4	5 150
A2	400	5	7	4 400	7
A3	150	9	8	9	4 150
A4	150	4	3 150	3	9
A5	300	6 150	5 150	6	8

Вычисляем значение целевой функции полученного начального решения:

R=7*100+6*150+3*150+5*150+4*400+5*150+4*150=5750 тыс. руб.

Видим, что это решение более целесообразное, чем полученное методом северо-западного угла. Но это не значит, что полученное решение оптимальное.
6.5. ПРОВЕРКА РЕШЕНИЯ НА ОПТИМАЛЬНОСТЬ
Перейдем ко второму этапу решения задачи — проверке полученного решения на оптимальность.

Решение будет оптимальным только тогда, когда целевая функция примет минимальное значение, т. е. когда дальнейшее уменьшение затрат путем перераспределения поставок будет невозможным.

Условимся называть клетки, заполненные поставками — базисными, клетки, где нет поставки — свободными.

Чтобы установить, является ли план оптимальным, надо проверить, можно ли уменьшить значение функции цепи перераспределив поставки. Для этого в каждую свободную клетку попытаемся включить какую-либо поставку, но с таким перераспределением начального решения, чтобы оно было допустимым, т. е. чтобы соблюдался баланс спроса и предложения. Если в результате таких перестановок найдется хотя бы одно решение, которое приведет к снижению величины функции цели, значит анализируемое решение не оптимальное.

---

В опорном плане, представленном в табл.3., имеется 13 свободных клеток, значит необходимо проверить возможность единичной поставки поочередно в каждую из этих клеток. Для выполнения этого анализа принимаем именно единичную поставку, так как при этом значительно упрощаются расчеты. В свободную клетку А4В1 поставим единичную поставку, т.е. приняв за основу начальное решение, проверим, будет ли уменьшена величина функции цели, если хотя бы 1 м3 (1 тыс. м3 ) пиловочника будет поставлен с леспромхоза А4 на предприятие В1.

Для того, чтобы не нарушался баланс поставщика А4 необходимо уменьшить поставку от этого поставщика потребителю В2 на единицу, но чтобы не нарушилась поставка потребителю В2, необходимо увеличить ему поставку от поставщика А5 на единицу. В свою очередь, чтобы не нарушился баланс поставщика А5 необходимо уменьшить от него поставку потребителю В1.

Результат этих перестановок можно изобразить схемой, приведенной на рис. 1. В результате выполненных перестановок мы опять получили допустимое решение. Стоимость поставки потребителю В1 от поставщика A4 т. е. cтоимость поставки A4В1 увеличится на

C41 = 4*1 = +4.

		B1	B2
		250	300
A4	150	4 +1	3 150 -1
A5	300	6 150 -1	5 150 +1

Рис.1
В целом, изменения, которые произойдут при рассмотренной перестановке поставок, можно записать следующим образом:

ΔR= +С41 *1- С42 *1 +С52 *1- С51 *1=+4-3+5-6=0

Проверим на оптимальность и переход от неоптимального решения к лучшему.

Клетка А1В2 ∑С12 = +6-5+6-7=0

Клетка А1В3 ∑С13 = клетка не проверяется

Клетка А2В1 ∑С21 = клетка не проверяется

Клетка А2В2 ∑С22 = клетка не проверяется

Клетка А2В4 ∑С24 = клетка не проверяется

Клетка А3В1 ∑С31 = +9-4+5-7= +3

---

Клетка А3В2 ∑С32 = +8-4+5-7+6-5=+3

Клетка А3В3 ∑С33 = клетка не проверяется

Клетка А4В1 ∑С41 = +4-3+5-6=0

Клетка А4В3 ∑С43 = клетка не проверяется

Клетка А4В4 ∑С44 = +9-5+7-6+5-3=+7

Клетка А5В3 ∑С53 = клетка не проверяется

Клетка А5В4 ∑С54 = +8-6+7-5=+4

РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ НА ЭВМ.

Для решения данной задачи используем программу Excel. Создаем в Excel две матрицы. В первой таблице введены единичные стоимости транспорта, а также формула для определения целевой функции. Во второй таблице записываем мощности поставщиков и спрос потребителей.


Целевая функция определяется по формуле:



(6.16)

Для решения транспортной задачи в таблице определения объемов перевозок, необходимо задать условия

1. Сумма объемов перевозок продукции, каждого поставщика, должна быть равна мощности этого поставщика.

2. Сумма объемов перевозок продукции, каждого потребителя, должна быть равна спросу потребителя.

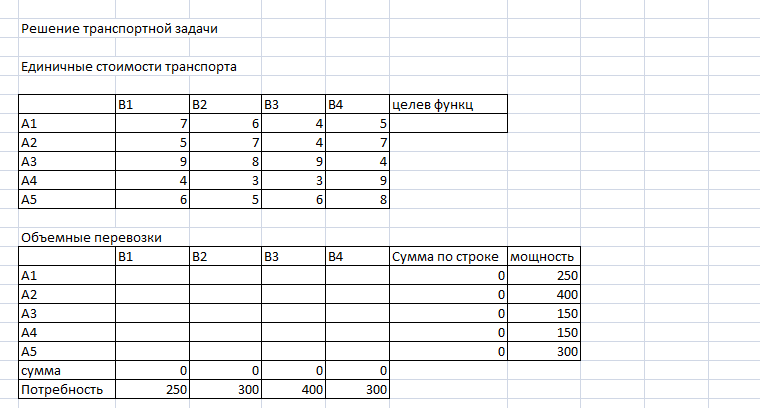
Для решения транспортной задачи в Microsoft Excel воспользуемся функцией «Поиск решений». В меню «Сервис», переходим в пункт «Надстройки», в доступных надстройках выбираем «Поиск решения».

При выполнении функции «Поиск решения» необходимо установить целевую ячейку, равной минимальному значению. Целевая ячейка задается в ячейке, где определяется целевая функция. Далее, указываем диапазон ячеек, где подбирается возможный вариант решений.

Задаем ограничения, согласно условиям транспортной задачи.



Исходные матрицы для решения транспортной задачи с формулами.



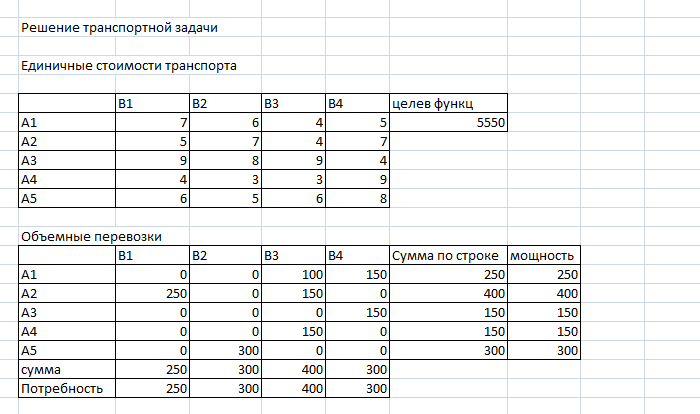
Результаты решения транспортной задачи.

Вывод: в ходе выполнения данной контрольной работы, была освоена методология планирования оптимальных грузопотоков лесопромышленного предприятия.

Так же было освоено построение опорного плана методом северо-западного угла, построение опорного плана по методу минимального элемента, проведена проверка на оптимальность и решение транспортной задачи на ЭВМ

---

, что оказалось самым эффективным и оптимальным.

---

Смотрите также файлы

• Контрольная работа по учебной дисциплине Делопроизводство и режим секретности.doc

• Материалы для подготовки к егэ Теория егэ по русскому языку Решать тесты егэ по русскому языку Содержание.docx

• Урок обучения грамоте. Садимся правильно, спинка прямая.docx

• Основы психологического консультирования клиента с рпп.docx

• Биологическая химия биохимия полости рта Раздел Белки и ферменты.docx