Файл: Методические указания к выполнению индивидуальных заданий по модулю для студентов инженерных специальностей.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приравнивая коэффициенты при одинаковых степенях неизвестной х слева и справа, получаем систему линейных уравнений
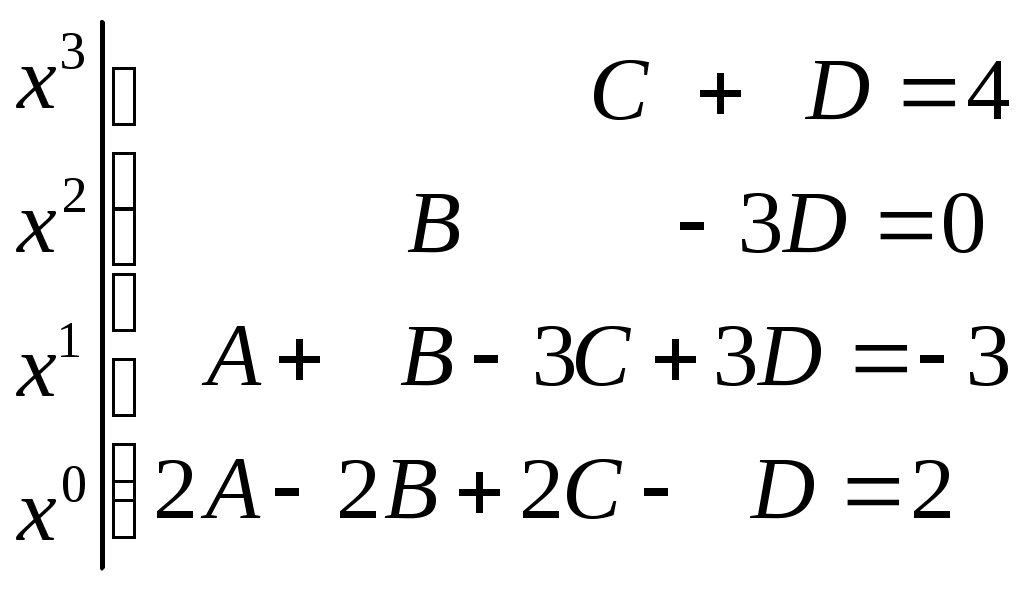
Решая эту систему, найдем
Примечание. Некоторые (а в случае простых корней знаменателя - все) значения коэффициентов могут быть найдены из тождества многочленов методом частных положений. Например, полагая в тождестве
последовательно 
, получим
Наиболее эффективным является, как правило, сочетание метода сравнения постепеням и метода частных положений.
-
Подстановка значений коэффициентов в разложение дроби на простейшие и интегрирование
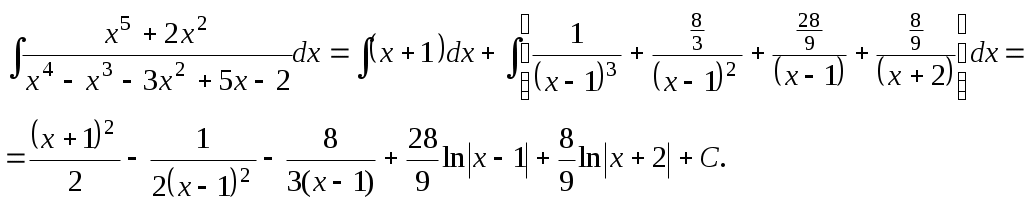
Задание 8. Интеграл, содержащий дробные степени одного и того же дробно-линейного выражения приводятся к интегралу от рациональной функции с помощью подстановки, представляющей это выражение в виде степени новой переменной, показатель которой равен наименьшему общему кратному знаменателей дробных степеней. После выполнения подстановки интегрирование проводится как в задании 7.
Пример 8.1. Найти интеграл
Решение. Так как наименьшее общее кратное чисел 2, 3, 6 равно 6, то выполняя замену
, 
, получим 
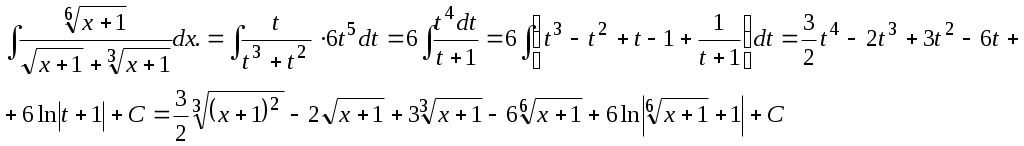Интегрирование рациональной функции, роль переменных которой играют основные тригонометрические функции 
производится с помощью универсальной тригонометрической подстановки 
.Пример 9.1. Найти интеграл
.
Решение. Полагая
, получим 
, 
, 
и, следовательно,
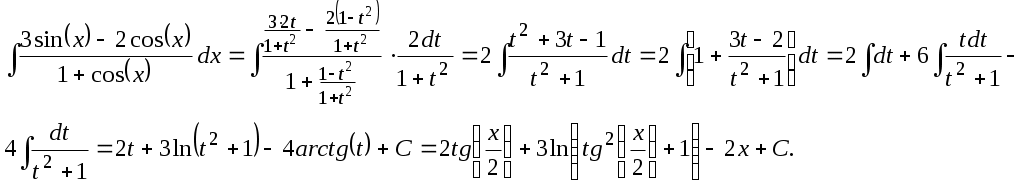Задание 10. Для вычисления интегралов вида 
используются тождественно соотношения между двойственными тригонометрическими функциями 
и их дифференциалами (если одна из степеней 
- положительная нечетная); формулы понижения 
, 
, 
, если оба показателя - положительные четные числа, выражение через функцию 
(или 
), если 
и 
- четное число.Пример 10.1. Найти интеграл
Решение. Учитывая, что
и 
, получаем
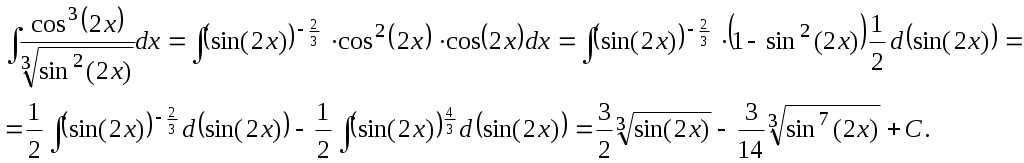
Пример 10.2. Найти интеграл
.
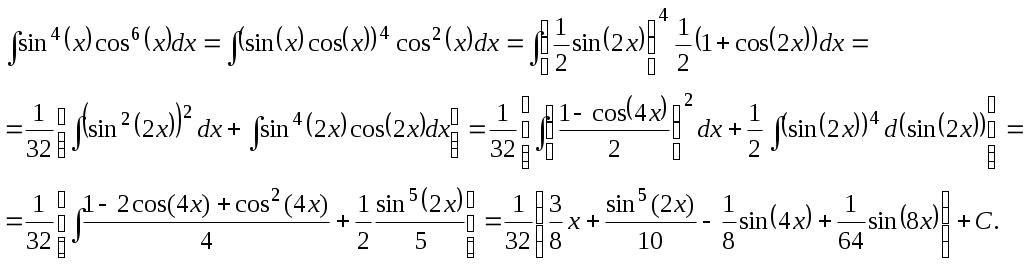
Литература
-
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. М.: Наука, 1988. -
Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 1. М.: Наука, 1976. -
Болгов В.А., Демидович Б.П., Ефимов А.В. и др. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа. М.: Наука, 1981. -
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Математический анализ в примерах и задачах. Ч. 1. Введение в анализ, производная, интеграл. Киев: Вища школа, 1974. -
Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.В. Сборник индивидуальных заданий по высшей математике. Ч.2 Минск: Высшая школа, 1991.