Файл: Изучение свойств активных фильтров на операционных усилителях.docx

Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради увеличения крутизны переходного участка, доводится до своего логического завершения в идее так называемого эллиптического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева. С помощью ЭВМ можно сконструировать эллиптические фильтры так же просто, как и классические фильтры Чебышева и Баттерворта. На рис. 7 представлено графическое задание амплитудно-частотной характеристики фильтра. В этом случае (фильтр нижних частот) определяются допустимый диапазон коэффициента передачи фильтра (т.е. неравномерность) в полосе пропускания, минимальная частота, на которой характеристика покидает полосу пропускания, максимальная частота, где характеристика переходит в полосу задерживания, и минимальное затухание в полосе задерживания.

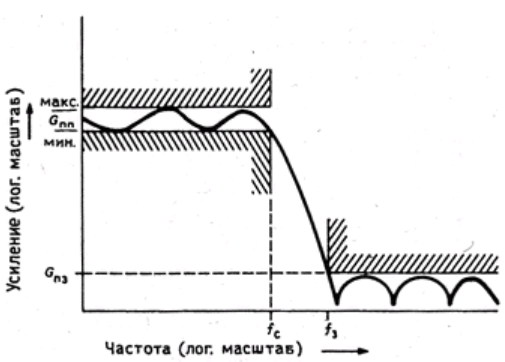
Рисунок 7 — Задание параметров частотной характеристики фильтра

Фильтры Бесселя. Как было установлено ранее, амплитудно-частотная характеристика фильтра не дает о нем полной информации. Фильтр с плоской амплитудно-частотной характеристикой может иметь большие сдвиги фаз. В результате этого форма сигнала, спектр которого лежит в полосе пропускания, будет искажена при прохождении через фильтр. В ситуации, при которой форма сигнала имеет первостепенное значение, желательно иметь в распоряжении линейно-фазовый фильтр (фильтр с постоянным временем запаздывания). Предъявление к фильтру требования обеспечения линейного изменения сдвига фазы в зависимости от частоты эквивалентно требованию постоянства времени запаздывания для сигнала, спектр которого расположен в полосе пропускания, т. е. отсутствия искажений формы сигнала. Фильтр Бесселя (также называемый фильтром Томсона) имеет наиболее плоский участок кривой времени запаздывания в полосе пропускания, подобно тому, как фильтр Баттерворта имеет наиболее плоскую амплитудно-частотную характеристику. Чтобы понять, какое улучшение во временной области дает фильтр Бесселя, посмотрите на рис. 8, где изображены нормированные по частоте графики времени запаздывания для 6-полюсных фильтров нижних частот Бесселя и Баттерворта. Плохая характеристика времени запаздывания фильтра Баттерворта обуславливает появление эффектов типа выброса при прохождении через фильтр импульсных сигналов. С другой же стороны, за постоянство времен запаздывания у фильтра Бесселя приходится расплачиваться тем, что его амплитудно-частотная характеристика имеет еще более пологий переходной участок между полосами пропускания и задерживания, чем даже у характеристики фильтра Баттерворта.

---

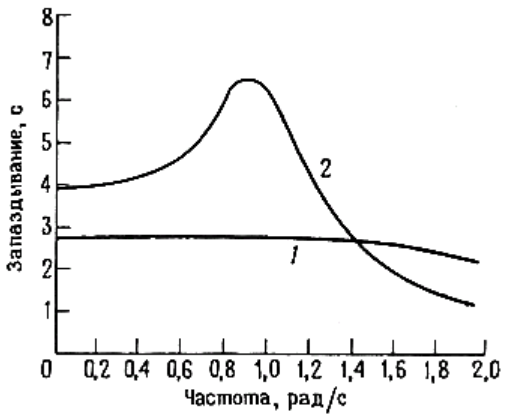
Рисунок 8 — Сравнение временных запаздываний для 6-полосных фильтров нижних частот Бесселя (1) и Баттерворта (2). Фильтр Бесселя благодаря своим превосходным свойствам во временной области дает наименьшее искажение формы сигнала

Существует много различных способов проектирования фильтров, в которых делаются попытки улучшить рабочие параметры фильтра Бесселя во временной области, частично жертвуя постоянством времени запаздывания ради уменьшения времени нарастания и улучшения амплитудно-частотной характеристики. Фильтр Гаусса имеет почти столь же хорошие фазочастотные характеристики, как и фильтр Бесселя, но при улучшенной переходной характеристике. Другой интересный класс представляют собой фильтры, позволяющие добиться одинаковых по величине пульсаций кривой времени запаздывания в полосе пропускания (аналогично пульсациям амплитудно-частотной характеристики фильтра Чебышева) и обеспечивающие примерно одинаковое запаздывание для сигналов со спектром вплоть до полосы задерживания. Еще один подход к созданию фильтров с постоянным временем запаздывания — это применение всепропускающих фильтров, называемых иначе корректорами во временной области. Эти фильтры обладают постоянной амплитудно-частотной характеристикой, а сдвиг фазы может меняться согласно конкретным требованиям. Таким образом, их можно применять для выравнивания времени запаздывания любых фильтров, в частности фильтров Баттерворта и Чебышева.

---

Сравнение фильтров.

Несмотря на ранее высказанные замечания о переходной характеристике фильтров Бесселя, он все же обладает очень хорошими свойствами во временной области по сравнению с фильтрами Баттерворта и Чебышева. Сам фильтр Чебышева при его весьма подходящей амплитудно-частотной характеристике имеет наихудшие параметры во временной области из всех этих трех типов фильтров. Фильтр Баттерворта дает компромисс между частотами и временными характеристиками. На рис. 9 дана информация по рабочим характеристикам этих трех типов фильтров во временной области, дополняющая приведенные ранее графики амплитудно-частотных характеристик. По этим данным можно сделать вывод, что в тех случаях, когда важны параметры фильтра во временной области, желательно применять фильтр Бесселя.

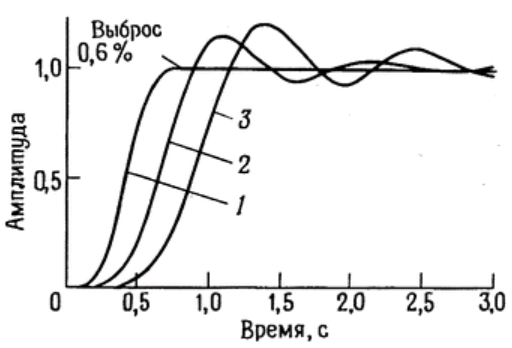
Рисунок 9 — Сравнение переходных процессов 6-полюсных фильтров нижних частот. Кривые нормированы приведением значения ослабления 3 дБ к частоте 1 Гц. 1 - фильтр Бесселя; 2 - фильтр Баттерворта; 3 - фильтр Чебышева (пульсации 0.5 дБ)

Известны очень хитроумные конструкции активных фильтров, каждый из которых используется для того, чтобы в качестве характеристики фильтра получить нужную функцию, как, например, функция Баттерворта, Чебышева и др. Можно спросить: зачем вообще нужно более одной схемы активного фильтра? Причина в том, что каждая схемная реализация является наилучшей в смысле тех или иных желательных свойств, и поэтому «абсолютно лучшей» схемы фильтра не существует.

Некоторые свойства, желательные для схемы активного фильтра, таковы:

1. малое число элементов, как активных, так и пассивных; 

2. легкость регулировки;

3. малое влияние разброса параметров элементов, в особенности значений емкостей конденсаторов;

4. отсутствие жестких требований к применяемому операционному усилителю, в особенности требований к скорости нарастания, ширине полосы пропускания и полному выходному сопротивлению;

5. возможность создания высокодобротных фильтров;

6. нечувствительность характеристик фильтра по отношению к параметрам элементов и коэффициенту усиления ОУ (в частности, произведению коэффициента усиления на ширину полосы пропускания, ƒ_с).

По многим причинам последнее свойство является одним из наиболее важных. Фильтр, который требует соблюдения высокой точности значений параметров элементов, трудно настраивать, и по мере старения элементов настройка теряется; кроме того, дополнительной неприятностью является требование использовать элементы с малым допуском значений параметров.

---

Схема фильтра на ИНУН (источник напряжения, управляемый напряжением) обязана широкой популярностью в основном своей простоте и малому числу деталей, но эта схема страдает недостатком, а именно высокой чувствительностью к изменениям значения параметров элементов. Для сравнения: недавно возникший интерес к более сложным гиратороподобным схемам вызван их нечувствительностью к малым изменениям параметров элементов.

В этом разделе будет рассмотрено несколько схем для реализации фильтров нижних и верхних частот, а также полосовых фильтров. Начнем же с популярной схемы на ИНУН, далее узнаем о двойном Т-образном фильтре с высоким избирательным подавлением («фильтр - пробка»).

Фильтр на источнике напряжения, управляемом напряжением (ИНУН), известный также просто как фильтр с управляемым источником — это вариант фильтра Саллена и Ки. В этом случае повторитель с единичным коэффициентом усиления заменен не инвертирующим усилителем с коэффициентом усиления, большим 1. На рис. 10 даны схемы для реализации фильтра нижних и верхних частот, а также полосового фильтра. С помощью присоединенных к выходу ОУ резисторов, образован не инвертирующий усилитель напряжения с коэффициентом усиления K, а остальные R и С по-прежнему формируют частотную характеристику фильтра. Как будет показано далее, эти двухполюсные фильтры могут быть фильтрами Баттерворта, Беселя и др. за счет определенного подбора параметров элементов. Любое число двухполюсных секций на ИНУН может быть соединено каскадно для создания фильтров более высокого порядка. В таком соединении отдельные секции, вообще говоря, не идентичны. Действительно, каждая секция соответствует квадратичному сомножителю полинома степени n, описывающего фильтр в целом.

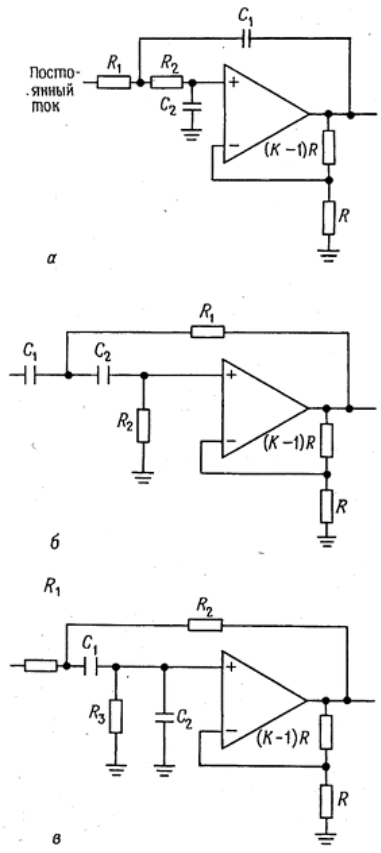
Рисунок 10 — Схемы активных фильтров на ИНУН. a — фильтр нижних частот; б — фильтр верхних частот; в — полосовой фильтр

В большинстве обычных справочников по фильтрам приведены формулы и таблицы для всех стандартных характеристик фильтров, включая отдельные таблицы для фильтров Чебышева с разными амплитудами пульсаций. Полосовой и полосноподавляюший фильтры легко могут быть составлены из их комбинаций.

Начало формы

Двойной Т-образный фильтр-пробка.

Изображенная на рис. 12 пассивная RC-цепь имеет бесконечное затухание на частоте, равной ƒ_c = 1/2πRC. Такое бесконечное ослабление для RC-фильтров, вообще говоря, не характерно - данный фильтр действует столь эффективно благодаря сложению двух сигналов, которые на частоте среза имеют разность фаз в 180°. Получение достаточно близкого к нулю значения характеристики на частоте ƒ_c требует хорошего согласования элементов. Этот фильтр называется двойным Т-образным и может употребляться для устранения сигнала помехи, например сетевой наводки 50 Гц. Трудность состоит в том, что характеристика этой цепи такая же «мягкая», как и у всех пассивных RC-цепей, и лишь в окрестности частоты ƒ_c обрывается почти отвесно. Например, двойная Т-образная цепь, управляемая идеальным источником напряжения, имеет затухание 10 дБ на частоте, равной удвоенной (или половинной) частоте ƒ_c, и ослабление 3 дБ на частоте, равной учетверенной (или деленной на четыре) частоте ƒ_c.

---

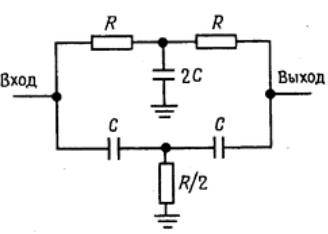
Рисунок 12 — Пассивный двойной Т-образный фильтр - пробка.

Один из способов улучшить характеристику этой цепи - сделать ее «активной» - по типу фильтра Саллена и Ки (рис. 13). Эта идея кажется в принципе хорошей, но на практике разочаровывает из-за невозможности сохранения хорошего затухания на частоте нуля. Дело в том, что при увеличении резкости провала характеристики (большее усиление в петле следящей связи) ослабление на частоте нуля уменьшается.

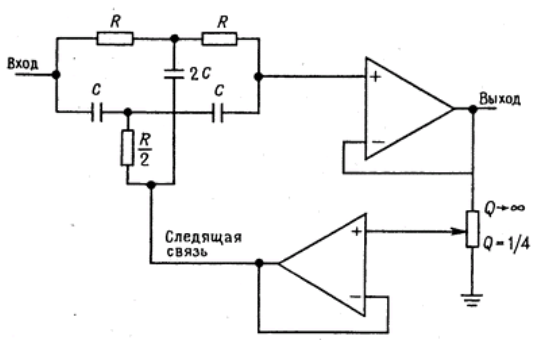
Рисунок 13 — Т-образный фильтр со следящей связью.

Двойные Т-образные фильтры выпускаются в виде готовых модулей на диапазон частот от 1 Гц до 50 кГц с глубиной ослабления на частоте провала около 60 дБ (с некоторым ухудшением при высоких и низких температурах). Такие фильтры легко собрать из отдельных элементов, но для получения глубокого и стабильного провала следует выбирать конденсаторы и резисторы со стабильными параметрами и низкой температурной зависимостью. Один из элементов должен быть регулируемым.

Ход выполнения лабораторной работы:

Простой ФВЧ первого порядка

Крутизна спада 20дБ на декаду

Используем стандартный ОУ OP_07, заданную частоту среза 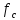берем примерно 1кГц

Определить частоту среза данного фильтра (рис. 14) можно, рассчитывая реактивное сопротивление конденсатора. Частота, при которой оно станет равным сопротивлению резистора, включенного последовательно с конденсатором, и будет частотой среза.

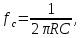
Пусть емкость конденсатора 10 нФ, тогда:

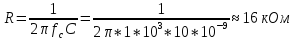
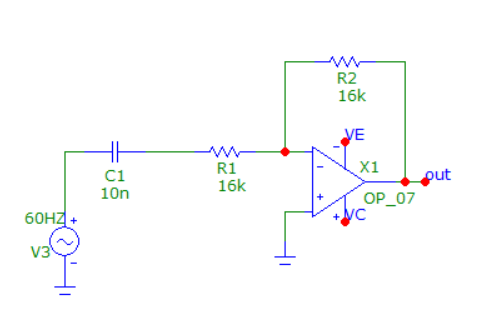
Рисунок 14 – ФВЧ первого порядка с крутизной спада 20 дБ на декаду

Частотные характеристики фильтра показаны на рисунке 15.

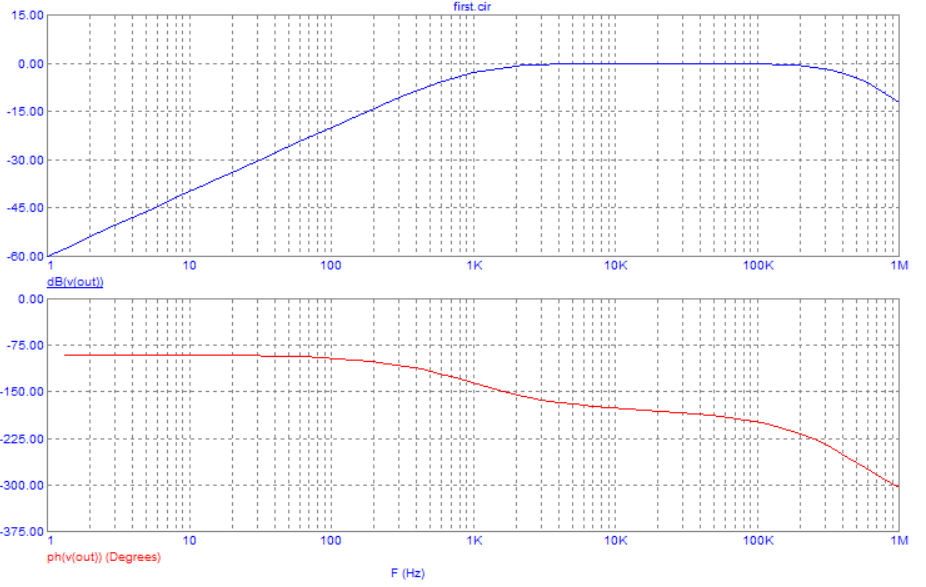
Рисунок 15 – ЛАЧХ и ЛФЧХ ФВЧ первого порядка с крутизной 20 дБ на декаду

Фильтр верхних частот второго порядка, крутизна спада характеристики 40дБ на декаду

---