Цель работы: освоить два метода приближенного определения оптимальных параметров дискретных ПИД регуляторов

Непрерывные системы уравнения

Задание

1. Найдите передаточные функции: разомкнутой Wpc(s) и замкнутой систем, а также главную передаточную функцию относительно ошибки и возмущения .

2. Постройте область устойчивости системы в плоскости общего

коэффициента передачи и постоянной времени при заданных значениях и . Найдите граничное значение при заданном значении , при котором система выходит на границу устойчивости.

3. Постройте графики логарифмической амплитуды и фазовых частотных

характеристик (ЛАЧХ и ЛФЧХ) и при значении коэффициента передачи .

4. Оцените запасы устойчивости по модулю и фазе , время переходного процесса tп и перерегулирование в исходной системе при

---

и v = 0.

5. Если исходная система не удовлетворяет заданным в табл. 2 показателям качества tп, , (хотя бы одному из них) или имеет малые запасы устойчивости, то проведите коррекцию системы (последовательного типа) и найдите передаточную функцию корректирующего устройства.

6. Вычислите в скорректированной системе переходный процесс на выходе при подаче на вход единичной ступенчатой функции y0(t) = 1(t). Найдите tп, переходного процесса и сравните их с заданными из табл. 2.


Методические указания
Структура исследуемой замкнутой линейной непрерывной САУ, где y0(t) - задающее воздействие, v(t) - возмущающее воздействие, - сигнал ошибки, - выходной сигнал.

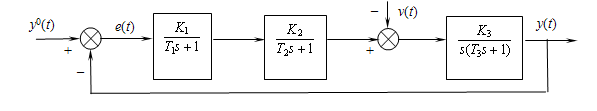
Значения параметров , , заданы в табл. Размерность , T2, T3 в секундах, общий коэффициент передачи имеет размерность 1/с, в табл. также приведены желаемые показатели качества системы: время переходного процесса tп в секундах, и перерегулирование в процентах при единичном скачке по каналу задания.
Таблица 1

Номер варианта	tп	, %
9	2.0	45	0.048	0.1	3

---

Определим передаточную функцию замкнутой линейной непрерывной САУ.
, .
Определим передаточную функцию разомкнутой системы при ν = 0

. (1)
После подстановки выражений передаточных функций W1(s), W2(s) и W3(s) получим
Wрс(s) = K/L(s),

где K = K1 K2 K3, L(s) = (T1s + 1) (T2s + 1) (T3s2 + s).
Передаточной функцией замкнутой системы W(s) будет выражение
(2)
Выведем передаточную функцию относительно ошибки

(s) = E(s)/Y 0(s). (3)
Выразим E(s) через E(s) = Y0(s) - Y(s), а Y(s) через Y(s) = E(s)∙W1(s) W2(s) W3(s) = E(s) Wрс(s). Подставим E(s) и Y(s) в формулу (3)


или We(s) + We(s)Wрс(s) = 1.

Отсюда получим передаточную функцию относительно ошибки
. (4)
и передаточную функцию относительно возмущения
(5)
при y0 = 0 получим следующим образом. Найдем выражение Y(s) = [-Y(s)W1(s) W2(s) - V(s)] W3(s), в котором перенесем в левую часть выражение -Y(s)W1(s) W2(s) W3(s) = Y(s) Wрс(s)
Y(s) + Y(s) Wрс(s) = - V(s)∙W3(s)
и выделим Y(s)
.
Подставляя последнее выражение в (5), получим
. (6)

регулятор синтез дискретный simulink

Если y0(t) ≠ 0 и ν(t) ≠ 0, то выход Y(s) в системе определится как алгебраическая сумма

Y(s) = W(s) Y0(s) - Wν(s) V(s).
Передаточная функция разомкнутой исходной системы имеет вид Wpc(s) = K/L(s). Характеристическим уравнением замкнутой системы будет

---

,
где b4 = K. При заданных в табл. 1 числовых значениях и коэффициенты bi будут зависеть от параметров и . Применение критерия Гурвица [1] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:
.

,



Wрс(s) = K/L(s),

где K = K1 K2 K3, L(s) = (0.048s + 1) (0.1s + 1) (3s2 + s).
Передаточная функция замкнутой системы



Отсюда получим передаточную функцию относительно ошибки
. (7)
и передаточную функцию относительно возмущения

При Т1 = 0.048, Т3 = 3, Т20, 0.1, K0, 10 определим границу устойчивости, используя пр. 1.

Пр. 1

dbpred=1;T1=0.048;T3=3; for T2=0:0.01:0.11;for K=0:0.005:10; b=conv(conv(conv([T1 1],[T2 1]),[T3 1]),[1 0]); b(5)=b(5)+K; db=b(4)*(b(2)*b(3)-b(1)*b(4))-b(5)*b(2)^2; if db*dbpred<0; hold on; plot(T2,K,'.'),grid xlabel('T2'),ylabel('K') hold off end; dbpred=db; end; end;

На рис. 1 приводится результат работы пр. 1 - граница области устойчивости в плоскости параметров K, T2, по которой определим предельное значение K= 6.945 при T2 = 0.1.

---

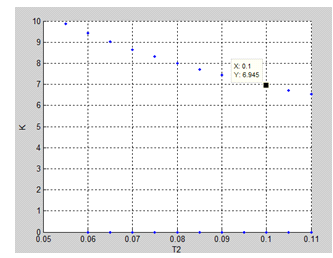
Рис. 1

При = 0.1 находим граничное значение = 7 коэффициента передачи K. Полагая = 4.9, находим выражение для , из при . Используя процедуру margin в пр. 2, строим графики логарифмических характеристик.

Пр. 2

T1=0.048;T2=0.1; T3=3;K=4.9; W1=tf([1],[T1 1]); W2=tf([1],[T2 1]); W3=tf([1],[T3 1 0]); W=K*W1*W2*W3; margin(W)

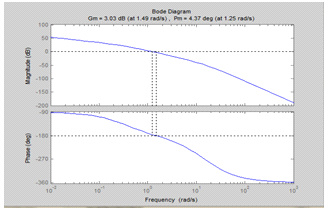
Рис. 2

Запасы устойчивости по модулю = 3.03 дб определяем на частоте ω = 1.49 рад/с, при которой , а запас устойчивости по фазе = 4.37 град - на частоте среза = 1.25 рад/с (рис. 2).

Для ориентировочной оценки tп и следует с помощью пр. 3 построить переходной процесс при y0 = 1(t) и из него определить tп (Settling time) и (Overshoot), представленные на рис. 3.

Пр. 3

T1=0.048;T2=0.1; T3=3;K=4.9; W1=tf([1],[T1 1]); W2=tf([1],[T2 1]); W3=tf([1],[T3 1 0]); Wpc=K*W1*W2*W3; W=feedback(Wpc,+1); step(W)

---

Смотрите также файлы

• Тестовые вопросы по тсп1.doc

• Потребительский выбор.doc

• В музыкальном театре 2класс.docx

• Консорциум.docx

• 68 Жібек жолы жалпы орта мектебі коммуналды мемлекеттік мекемесі 4 сынып оушыларыны ббжм тест орытындысыны сараптамасы.docx