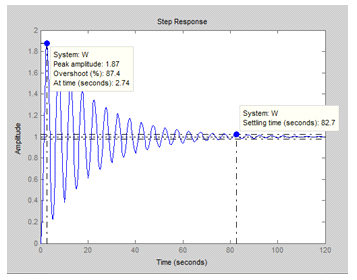
Рис. 3
Поместим полученные расчетные и заданные значения показателей качества переходного процесса в табл. 2. Из неё видно, расчетные значения показателей качества переходного процесса tп, значительно отличаются от заданных, т.е. система нуждается в коррекции.

Таблица 2

Значения показателей	tп, с	, %	, град	, Дб
Заданные	2	45	30< <60	6< <20
Расчетные	82.7	87.4	4.37	3.03

Выполнение работы
На рис. 4 изображена исходная динамическая система, описываемая передаточной функцией (ПФ):


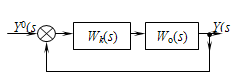
Передаточная функция не удовлетворяет требуемым показателям качества:

. Перерегулирование: σ ≤ 45%.

. Время переходного процесса tп≤ 2).

. Запас устойчивости по фазе 30< <60.

. Запас устойчивости по модулю 6< <20, нуждается в последовательном включении и настройке корректирующего устройства с начальной ПФ, изображенной на рис. 4,
Wk(s) = Kk(s ‒ z)/(s ‒ p),
где Kk = 1, z = ‒1, p = ‒2.

Синтез корректирующего устройства будем осуществлять методом корневого годографа (КГ) с помощью программы rltool пакета MATLAB

---

Определим в пр. 4 передаточные функции объекта Wo(s) и компенсатора Wk(s) в виде, пригодном для дальнейшего использования.

Пр. 4

T1=0.048;T2=0.1; T3=3;K=4.9; W1=tf([1],[T1 1]); W2=tf([1],[T2 1]); W3=tf([1],[T3 1 0]); Wo=K*W1*W2*W3 Wk=tf([1 1],[1 2])

В командную строку введем rltool и нажмем Enter. Появятся два окна "SISO Desing for SISO Desing Task" и "Control and Estmation Tools Manager",.показанные на рис. 5а и 5б.


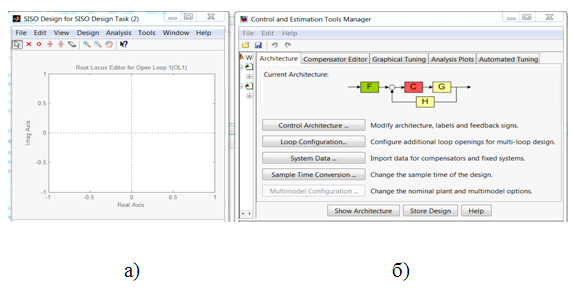
Рис. 5

В окне на рис. 5б нажмем кнопку System Data и откроется одноименное окно, изображенное на рис. 6, в которую импортируем данные передаточной функции объекта Wо(s) в поле G.



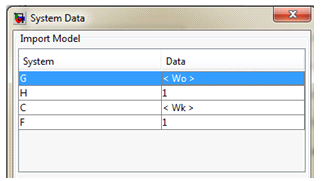
Рис. 6

Для этого в столбце System выделим строку с G и нажмем Browse.Появится окно "Model Import", изображенное на рис. 7, в котором устанавливаем переключатель Import from Workspace, затем выделяем строчку с Wo в столбце Available Models и нажмем последовательно кнопки Import и Close.

Аналогичные действия производятся с импортом передаточной функции корректирующего звена Wk(s) в поле С. Затем в окне "System Data" нажмем ОК.


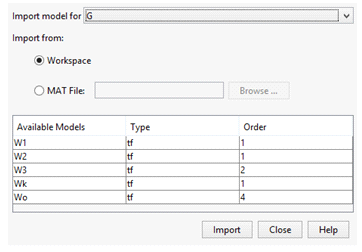
Рис. 7
В окне на рис. 5а с помощью команды Edit, SISO Tool Preferences, открываем окно "SISO Tool Preferences".

На вкладке Options, изображенной на рис. 8, сформируем формат компенсирующего звена, установив переключатель в положение Zero/pole/gain.



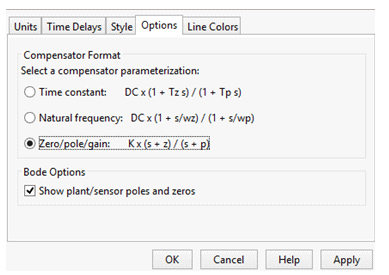
Рис. 8
В окне "SISO Design for SISO Design Task", изображенном на рис. 9, появится график корневого годографа (Root Locus). В рабочем поле корневого годографа правой кнопкой мыши вызываем контекстное меню и выполним команду Design Requirements, New. В появившемся окне "New Design Requirements", изображенном на рис. 11, в строке Design requirements type: выберем Settling time (время переходного процесса), а в строке Settling time ≤ введем 2. Аналогичным образом в окне "New Design Requirements" выберем Percent overshoot (перерегулирование) и установим 45%, изображенное на рис. 10.



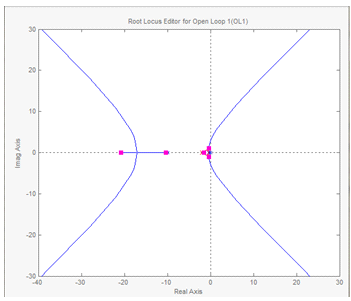
Рис. 9


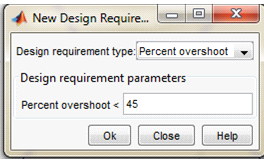
Рис. 10

---

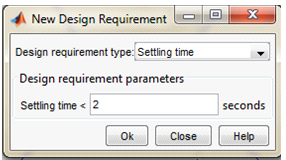
Рис. 11
На графике корневого годографа, изображенного на рис. 12, выделится область, соответствующая недопустимому расположению доминирующих полюсов замкнутой системы.



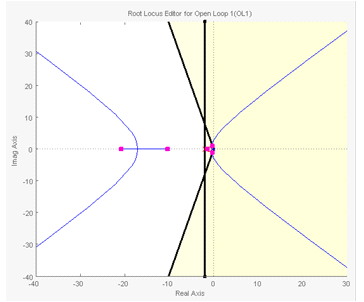
Рис. 12
В окне "Control and Estimation Tool Manager" открываем вкладку Automated Tuning, нажимаем кнопку Optimize Compensator и открываем вкладку Compensators, помечаем флажками элементы компенсатора (Gain) (коэффициент Kk), Real Zero (вещественный ноль z) и Real Pole (вещественный полюс p), подлежащие коррекции.

Нажмем кнопку Start Optimization и наблюдаем за развитием процесса оптимизации элементов компенсатора. Ее результаты можно получить, вторично открыв вкладку Compensators, изображенную на рис. 13.


Рис. 13
Полученные параметры подставляем в передаточную функцию

.

На основании полученных передаточных функций объекта Wo(s) и корректирующего звена Wk(s) определим ПФ замкнутой системы W(s) = Wo(s)Wk(s)/(1 + Wo(s)Wk(s)) и ее переходную функцию, изображенную на рис. 14. Здесь время переходного процесса tп (Settling time), равное 1.23, меньше заданного 2, а перерегулирование σ (Overshoot), равное 11.4% меньше заданного 45%, следовательно полученная система удовлетворяет принятым условиям. В таблице 3 представлены расчетные данные, которые полностью удовлетворяют заданным.

Таблица 3

Значения показателей	tп, с	, %	, град	, Дб
Заданные	2	45	30< <60	6< <20
Расчетные	1.23	11.4	43.8	10.9

---

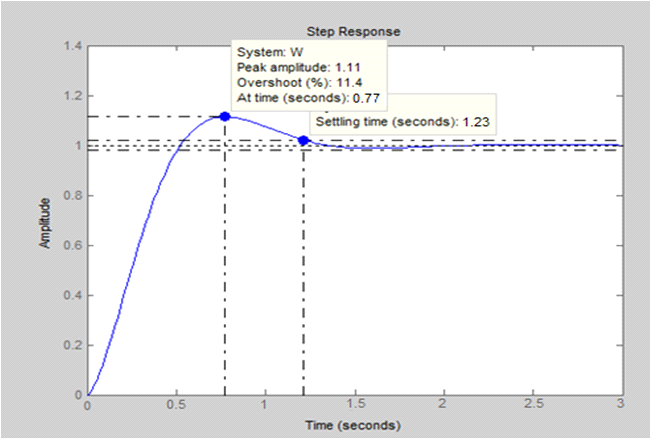
Рис. 14
Запасы устойчивости по модулю ∆L = 10.9 и фазе ∆φ = 43.8, изображенные на рис. 15, которые удовлетворяют заданным условиям.


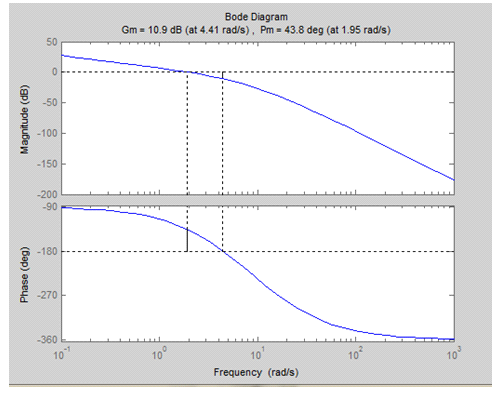
Рис. 15

Синтез дискретных систем управления
Задание
Структура исследуемой замкнутой линейной непрерывной САУ с дискретным PID регулятором представлена на рис. 16, где Y0 - задающее воздействие, - сигнал ошибки, - выходной сигнал.

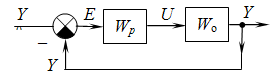
Значения параметров Kо, , , ПФ объекта, заданной соотношением:
,
В табл. 1 также приведены желаемые показатели качества системы: время переходного процесса tп в секундах и перерегулирование в процентах при единичном скачке по каналу задания.

В работе предлагаются два достаточно простых метода определения оптимальных параметров дискретного PID регулятора, реализованных в MATLAB и SUMULINK и использующих объект управления с передаточной функцией.
Выполнение работы
Создадим в библиотеке SIMULINK модель дискретной замкнутой системы управления (рис. 17), содержащей непрерывный объект управления с передаточной функцией и дискретным PID регулятором PID(z).


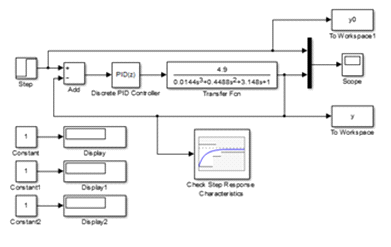
Рис. 17
Зададим время моделирования simulation stop time равным 50. Двойным щелчком по блоку PID(z) откроем окно "Function Block Parameters", в правой части которого находится формула, описывающая PID регулятор

---

.
Щелчком правой кнопки по блоку регулятора откроем контекстное меню, выберем в нем пункт Open In New Window и выведем схему дискретного PID регулятора, изображенного на рис. 18.


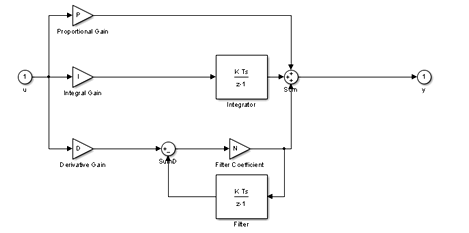
Рис. 18
В традиционном PID регуляторе отсутствует коэффициент N, поэтому при дальнейшей настройке параметров регулятора зададим его равным 1.

Двойным щелчком по блоку PID(z) откроем окно задания параметров регулятора "Function Block Parameters: PID Controller", изображенный на рис. 19.


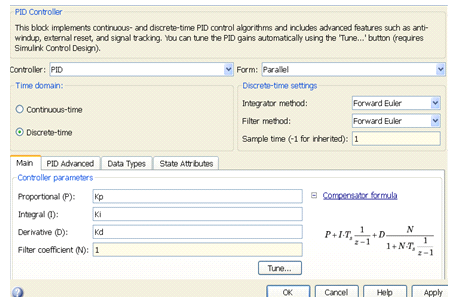
Рис. 19
Выберем дискретный (Discrete-time) PID регулятор. В поле Sample time задаем значение 1. На вкладке Main задаем пропорциональную, интегральную и дифференциальную составляющие регулятора в виде переменных Kp, Ki, Kd, а Filter coefficient N установим равным 1. Параметры регулятора заданы в виде переменных, чтобы их настраивать с помощью дополнительных средств Simulink. Эти переменные видимы в рабочей области MATLAB. В командной строке введем начальные значения Kp = 1, Kd = 1, Ki = 1. Запустим процесс симуляции и получим график переходного процесса, изображенный на рис. 20.


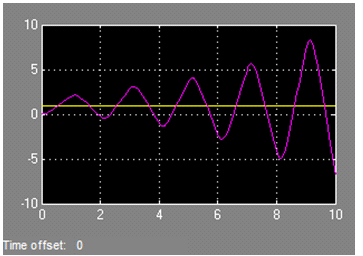
Рис. 20
Снизить перерегулирование с помощью кнопки Tune в окне настройки параметров регулятора "Function Block Parameters: PID Controller" удается лишь в том случае, когда коэффициент N остается равным единице. Для повышения качества переходного процесса воспользуемся надстройкой Response Optimization. Для этого двойным щелчком по блоку Check Step Response Characteristics на схеме модели откроем окно задания параметров блока "Sink Block Parameters: Check Step Response Characteristics", изображенное на рис. 21 и введем границы выходного сигнала: время нарастания (Rise time) - не более 5 с и длительность переходного процесса (Setting time) - не более 15 с.



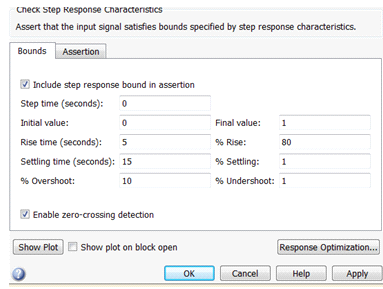
Рис. 21
Для выбора дополнительных параметров оптимизации нажмем кнопку Response Optimization и откроем окно "Design Optimization", изображенное на рис. 22.


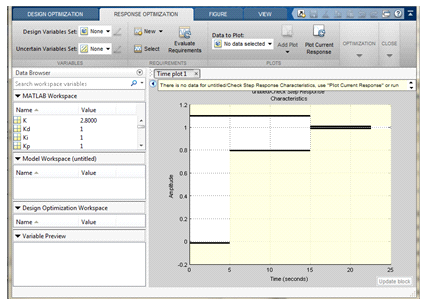
Рис. 22

В правой части окна "Design Optimization" изображены горизонтальные линии ограничений, задающие границы выходного сигнала: время нарастания и длительность переходного процесса, значения которых можно менять, двигая курсором мыши. Выделим выходные данные, которые будут отображаться на графике, для этого на вкладке Response Optimization в поле Data to Plot выберем опцию PID/Check Step Response Characteristics.

---

Смотрите также файлы

• Тестовые вопросы по тсп1.doc

• Потребительский выбор.doc

• В музыкальном театре 2класс.docx

• Консорциум.docx

• 68 Жібек жолы жалпы орта мектебі коммуналды мемлекеттік мекемесі 4 сынып оушыларыны ббжм тест орытындысыны сараптамасы.docx