Добавлен: 27.03.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Следует отметить, что LDPC-кодирование не является сугубо теоретической разработкой, а уже активно используется и введено в некоторые стандарты. Например, в 2003г. LDPC-код вместо турбо-кода стал частью стандарта DVB-S2 спутниковой передачи данных для цифрового телевидения. Аналогичная замена произошла и в стандарте DVB-T2 для цифрового наземного телевизионного вещания. Также LDPC-коды вошли в стандарт IEEE 802.3an сети Ethernet 10G и другие.
По результатам исследования среди кодов для включения в стандарт DVB-S2 были отмечены следующие преимущества:
-
отставание от границы Шеннона всего на 0,6–0,8 дБ; -
преимущество на 0,3 дБ по сравнению с лучшим из представленных турбо-кодов; -
преимущество на 2,5–3,0 дБ, т. е. 30-процентный прирост в мощности, по сравнению со стандартом DVB-S.
Были проведены моделирование работы недвоичных LDPC-кодов и сравнение их производительности с производительностью кодов Рида–Соломона. Результаты моделирования показали, что недвоичные LDPC-коды имеют существенное преимущество над кодами Рида–Соломона. Это преимущество увеличивается по мере увеличения длины кода и разрядности символа.
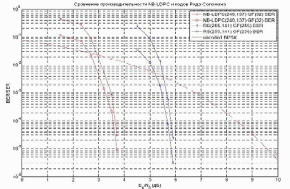
Рисунок. 5. Сравнение производительности NB-LDPC и кодов Рида–Соломона при средней длине блока
Далее рассмотрим алгоритм алгоритмов декодирования — алгоритма Belief propagation (aka SPA — Sum-product algorithm)
-
Алгоритм Belief propagation
Распространение убеждения, также известное как передача сообщения сумма-произведение, представляет собой передачу сообщений алгоритм для выполнения вывода на графических моделях, таких как байесовские сети и случайные поля Маркова. Он вычисляет маргинальное распределение для каждого ненаблюдаемого узла (или переменной) в зависимости от любых наблюдаемых узлов (или переменных). Распространение веры обычно используется в искусственном интеллекте и теории информации и продемонстрировало эмпирический успех во многих приложениях, включая коды проверки четности с низкой плотностью, турбо коды, приближение свободной энергии и выполнимость.Алгоритм был впервые предложен Judea Pearl в 1982 году, который сформулировал его как алгоритм точного вывода на деревья, который позже был расширен до многодеревьев. Хотя он не является точным на общих графиках, он оказался полезным приближенным алгоритмом.
Если X = {X i } - это набор дискретных случайные величины с соединением функцией масс p, предельное распределение одного X i - это просто суммирование p по всем остальным переменным:
p X i (xi) = ∑ x ′: xi ′ = xip (x ′). {\ displaystyle p_ {X_ {i}} (x_ {i}) = \ sum _ {\ mathbf {x} ': x' _ {i} = x_ {i}} p (\ mathbf {x} '). }
Однако это быстро становится недопустимым с точки зрения вычислений: если имеется 100 двоичных переменных, то нужно суммировать более 2 ≈ 6,338 × 10 возможных значений. Используя структуру многодерева, распространение убеждений позволяет намного более эффективно вычислять маргинальные значения.
Варианты алгоритма распространения убеждений существуют для нескольких типов графических моделей (в частности, байесовских сетей и марковских случайных полей ). Мы описываем здесь вариант, который работает на факторном графике . Факторный граф - это двудольный граф , содержащий узлы, соответствующие переменным V и факторам F, с ребрами между переменными и факторами, в которых они появляются. Мы можем записать совместную функцию масс:
p (x) = ∏ a ∈ F fa (xa) {\ displaystyle p (\ mathbf {x}) = \ prod _ {a \ in F} f_ {a}
( \ mathbf {x} _ {a})}
где xa – это вектор соседних узлов переменных к факторному узлу a. Любая байесовская сеть или случайное поле Маркова может быть представлена в виде факторного графа, используя коэффициент для каждого узла с его родителями или коэффициент для каждого узла с его окрестностями соответственно.
Алгоритм работает, передавая функции с действительным знаком, называемые сообщениями, вместе с ребрами между скрытыми узлами. Точнее, если v - переменный узел, а a - факторный узел, связанный с v в факторном графе, сообщения от v до a, (обозначаются μ v → a {\ displaystyle \ mu _ {v \ to a}}
) и от a до v (μ a → v {\ displaystyle \ mu _ {a \ to v}} ) -являются функциями с действительным знаком, domain - это Dom (v), набор значений, которые может принимать случайная величина, связанная с v. Эти сообщения содержат «влияние», которое одна переменная оказывает на другую. Сообщения вычисляются по-разному в зависимости от того, является ли узел, получающий сообщение, узлом переменной или узлом фактора. Сохранение той же записи:-
Сообщение от переменной узла v к факторному узлу a является продуктом сообщений от всех других соседних факторных узлов (кроме получателя; в качестве альтернативы можно сказать, что получатель отправляет как сообщение, постоянная функция равна к «1»):
∀ xv ∈ D om (v), μ v → a (xv) = ∏ a ∗ ∈ N (v) ∖ {a} μ a ∗ → v (xv). {\ Displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {v \ to a} (x_ {v}) = \ prod _ {a ^ {*} \ in N (v) \ setminus \ {a \}} \ mu _ {a ^ {*} \ to v} (x_ {v}).}
где N (v) - это набор соседних (факторных) узлов для v. Если N (v) ∖ {a} {\ displaystyle N (v) \ setminus \ {a \}}
пусто, тогда μ v → a (xv) {\ displaystyle \ mu _ {v \ to a} (x_ {v})} устанавливается на равномерное распределение.-
Сообщение от факторного узла a до переменного узла v является произведением фактора с сообщениями от всех других узлов, маргинализовано по всем переменным, кроме одной, связанной с v:
∀ xv ∈ D om (v), μ a → v (xv) = ∑ xa ′: xv ′ = xvfa (xa ′) ∏ v ∗ ∈ N (a) ∖ {v} μ v ∗ → a (xv ∗ ′). {\ displaystyle \ forall x_ {v} \ in Dom (v), \; \ mu _ {a \ to v} (x_ {v}) = \ sum _ {\ mathbf {x} '_ {a}: x '_ {v} = x_ {v}} f_ {a} (\ mathbf {x}' _ {a}) \ prod _ {v ^ {*} \ in N (a) \ setminus \ {v \}} \ mu _ {v ^ {*} \ to a} (x '_ {v ^ {*}}).}
где N (a) - это набор соседних (переменных) узлов для a. Если N (a) ∖ {v} {\ displaystyle N (a) \ setminus \ {v \}}
пусто, то μ a → v (xv) = fa (xv) {\ displaystyle \ mu _ {a \ to v} (x_ {v}) = f_ {a} (x_ {v})} , поскольку в этом случае xv = xa {\ displaystyle x_ {v} = x_ {a}} .Как показывает предыдущая формула: полная маргинализация сводится к сумме произведений более простых условий, чем те, которые присутствуют в полном совместном распределении. По этой причине он называется алгоритмом сумм-произведений.
При типичном запуске каждое сообщение будет обновляться итеративно из предыдущего значения соседних сообщений. Для обновления сообщений можно использовать другое расписание. В случае, когда графическая модель представляет собой дерево, оптимальное планирование позволяет достичь сходимости после вычисления каждого сообщения только один раз (см. Следующий подраздел). Когда факторный граф имеет циклы, такого оптимального расписания не существует, и типичным выбором является одновременное обновление всех сообщений на каждой итерации.
После сходимости (если сходимость произошла) предполагаемое предельное распределение каждого узла пропорционально произведению всех сообщений от смежных факторов (без нормировочной константы):
p X v (xv) ∝ ∏ a ∈ N (v) μ a → v (xv). {\ displaystyle p_ {X_ {v}} (x_ {v}) \ propto \ prod _ {a \ in N (v)} \ mu _ {a \ to v} (x_ {v}).}
Аналогичным образом, оцененное совместное маргинальное распределение набора переменных, принадлежащих одному фактору, пропорционально произведению фактора и сообщений от переменных:
p X a (xa) ∝ fa (xa) ∏ v ∈ N ( а) μ v → a (xv). {\ displaystyle p_ {X_ {a}} (\ mathbf {x} _ {a}) \ propto f_ {a} (\ mathbf {x} _ {a}) \ prod _ {v \ in N (a)} \ mu _ {v \ to a} (x_ {v}).}
В случае, когда факторный граф является ациклическим (то есть является деревом или лесом), эти оцененные маргиналы фактически сходятся к истинным маргиналам в конечное количество итераций. Это можно показать с помощью математической индукции.
Точного алгоритма для деревьев
В случае, когда граф факторов является деревом, алгоритм распространения убеждений вычислит точные маргиналы. Кроме того, при правильном планировании обновлений сообщения оно прекратится после 2 шагов. Это оптимальное планирование можно описать следующим образом:
Перед запуском граф ориентируется путем назначения одного узла в качестве корня; любой некорневой узел, который связан только с одним другим узлом, называется листом.
На первом этапе сообщения передаются внутрь: начиная с листьев, каждый узел передает сообщение вдоль (уникального) края к корневому узлу. Древовидная структура гарантирует, что можно получить сообщения от всех других прилегающих узлов до передачи сообщения. Это продолжается до тех пор, пока корень не получит сообщения от всех своих соседних узлов.
Второй шаг включает передачу сообщений обратно: начиная с корня, сообщения передаются в обратном направлении. Алгоритм завершается, когда все листья получили свои сообщения.
Приближенный алгоритм для общих графов- изначально был разработан для ациклических графических моделей, было обнаружено, что алгоритм распространения веры может использоваться в общих графах. Затем алгоритм иногда называют зацикленным распространением убеждений, потому что графы обычно содержат циклы или циклы. Инициализация и планирование обновлений сообщений должны быть немного скорректированы (по сравнению с ранее описанным расписанием для ациклических графов), потому что графы могут не содержать листьев. Вместо этого каждый инициализирует все сообщения переменных в 1 и использует те же определения сообщений, что и выше, обновляя все сообщения на каждой итерации (хотя сообщения, поступающие из известных листьев или подграфов с древовидной структурой, могут больше не нуждаться в обновлении после достаточных итераций). Легко показать, что в дереве определения сообщений этой модифицированной процедуры будут
сходиться к набору определений сообщений, приведенных выше, в течение количества итераций, равных диаметру дерева.
Точные условия, при которых будет сходиться ненадежное распространение убеждений, до сих пор не совсем понятны; известно, что на графах, содержащих один цикл, в большинстве случаев он сходится, но полученные вероятности могут быть неверными. Существует несколько достаточных (но не необходимых) условий для сходимости зацикленного распространения убеждений к единственной фиксированной точке. Существуют графы, которые не могут сойтись или которые будут колебаться между несколькими состояниями при повторяющихся итерациях. Такие методы, как диаграммы ВЫХОДА, могут предоставить приблизительную визуализацию прогресса распространения убеждений и приблизительный тест на сходимость.
Существуют и другие приближенные методы маргинализации, включая вариационные методы и методы Монте-Карло.
Один метод точной маргинализации в общих графах называется алгоритмом дерева соединений, что является простым распространением убеждений на модифицированном графе, который гарантированно является деревом. Основная предпосылка - исключить циклы путем их кластеризации в отдельные узлы.
Связанные алгоритмы и проблемы сложности - подобный алгоритм обычно называют алгоритмом Витерби, но также известен как частный случай max-product или min- алгоритм суммы, который решает связанную проблему максимизации или наиболее вероятного объяснения. Вместо попытки решить маргинальное значение здесь цель состоит в том, чтобы найти значения x {\ displaystyle \ mathbf {x}}
, которые максимизируют глобальную функцию (т.е. наиболее вероятные значения в вероятностной настройке), и его можно определить с помощью arg max :* arg max xg (x). {\ displaystyle \ operatorname {*} {\ arg \ max} _ {\ mathbf {x}} g (\ mathbf {x}).}
Алгоритм, который решает эту проблему, почти идентичен распространению убеждений, с суммы заменены на максимумы в определениях.
Стоит отметить, что проблемы вывода, такие как маргинализация и максимизация, NP-трудны для точного и приближенного решения (по крайней мере, для относительная ошибка ) в графической модели. Точнее, проблема маргинализации, определенная выше, - это # P-complete, а максимизация - NP-complete.
Использование памяти для распространения убеждений может быть уменьшено за счет использования алгоритма Island. (с небольшими затратами по времени).