Добавлен: 28.03.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГУАП
КАФЕДРА № 41
ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
| ассистент | | | | Н. В. Апанасенко |
| должность, уч. степень, звание | | подпись, дата | | инициалы, фамилия |
| ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ |
| АНАЛИЗ РАБОТЫ ЭЛЕМЕНТАРНОЙ СИСТЕМЫ МНОЖЕСТВЕННОГО ДОСТУПА НА ОСНОВЕ АППАРАТА МАРКОВСКИХ ПРОЦЕССОВ |
| по курсу: ВЫЧИСЛИТЕЛЬНЫЕ СЕТИ, СИСТЕМЫ И ТЕЛЕКОММУНИКАЦИИ |
| |
| |
РАБОТУ ВЫПОЛНИЛ
| СТУДЕНТ ГР. № | 4017 | | | | А.А. Леонтьева |
| | | | подпись, дата | | инициалы, фамилия |
Санкт-Петербург 2022
Цель работы: анализ работы элементарной системы множественного доступа. Оценка среднего количества абонентов, находящихся в системе.
Краткие теоретические сведения:
Вероятности переходов из одного состояния в другое:
1. Вероятность перехода из состояния «ноль» в произвольное состояние j.
Переход из состояния 0 в состояние j может произойти, только когда количество абонентов, у которых появилось сообщение будет равно j, то есть
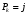. Так как 
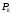распределено по закону Пуассона получаем: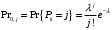
2. Вероятность перехода из i-го состояния в i-1.
Событие перехода из состояния i в состояние i-1 означает, что новых абонентов не появилось, и один абонент передал сообщение. То есть
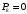
и
:
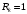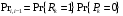
Вероятность «успеха» (один абонент передавал, остальные не передавали), определяется как:
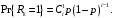
Вероятность отсутствия новых абонентов определяется как:
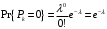
3. Вероятность остаться в состоянии i.
Переход из состояния i в i. может произойти в случае, если один абонент передал сообщение, и один новый абонент появился, или если новых абонентов не было, и ни один не передал:
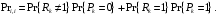
Вероятность того, что ни один абонент не передал сообщение определяется как:
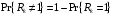
4. Вероятность перехода из состояния i в состояние j.
Переход из состояния i в j может произойти в случае, если один абонент передал сообщение и появились (j-i+1) абонентов, или если ни один не передал сообщение и появились (j-i) абонентов. Вероятность данного события определяется как:
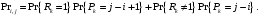
Используя описанные выше вероятности переходов из одного состояния в другое, можно сформировать систему усеченных линейных уравнений, для фиксированного значения
:
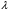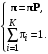
Решая данную систему усеченных линейных алгебраических уравнений (количество уравнений K), для фиксированного
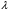, можно получить вектор стационарного распределения, каждое из значений 
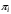означает вероятность того, что в системе находится i абонентов.Тогда оценить среднее количество абонентов, находящихся в системе множественного доступа можно как:
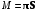,где
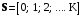.Выполнение работы
Код программы представлен в приложении А.
Создана матрица переходных состояний для 10 слотов и λ=0.05 (рисунок 1).
Рисунок 1 - Матрица переходных состояний
Найдены коэффициенты перед pi, после чего решена система линейных уравнений (рисунок 2).
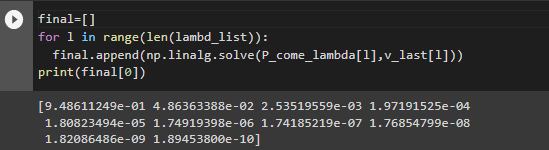
Рисунок 2 – Решение системы линейных уравнений
Высчитано среднее количество абонентов (рисунок 3).
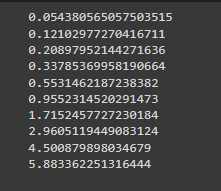
Рисунок 3 – Среднее количество абонентов
Построены графики зависимости среднего количества абонентов от значения входного потока. На этой же системе координат построен график из первой лабораторной работы (рисунок 4-7).
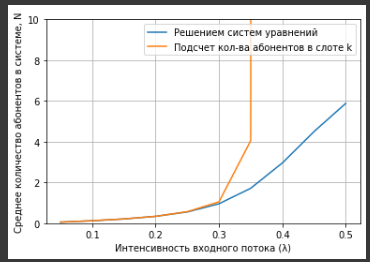
Рисунок 4 – График зависимости среднего количества абонентов от значения входного потока для 10 слотов
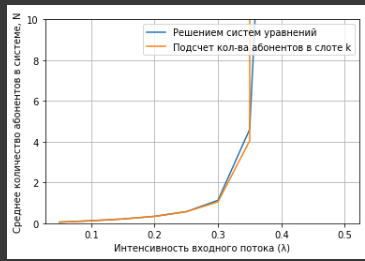
Рисунок 5 – График зависимости среднего количества абонентов от значения входного потока для 50 слотов
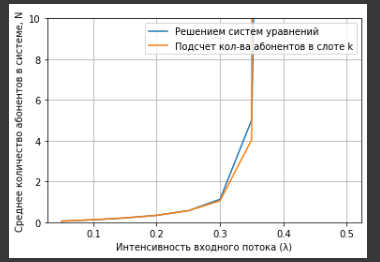
Рисунок 6 – График зависимости среднего количества абонентов от значения входного потока для 100 слотов
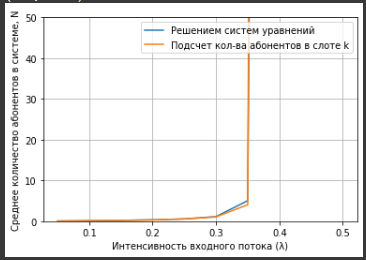
Рисунок 6 – График зависимости среднего количества абонентов от значения входного потока для 1000 слотов
При значении входного потока от
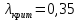среднее количество абонентов линейно возрастает, так как вероятность появления пользователя в слоте тоже линейно возрастает. После значения 0,35 графики расходятся.Дополнительное задание
Листинг дополнительного задания представлен в приложении Б.
Написать критерий Смирного-Колмогорова для одной выборки, которая является нормальным распределением и сортирована вставкой.
ВыводЯ изучила способы нахождения стационарного распределения Марковской цепи с конечным числом состояний и получила навыки моделирования Марковских цепей.
Сделан вывод, что от
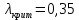среднее количество абонентов линейно возрастает, так как вероятность появления пользователя в слоте тоже линейно возрастает.ПРИЛОЖЕНИЕ А
Листинг программы
import numpy as np
import matplotlib.pyplot as plt
import math
import random
from random import randint
from scipy.stats import poisson
from scipy.stats import binom
l = 0 #интенсивность входного потока
lambd_list = []
for i in range(10):
l += 0.05
lambd_list.append(l)
k = 100000 # количество слотов
P_come_lambda = [] # количество абонентов, которое пришло в слот
for i in range(len(lambd_list)):
P_come_lambda.append(np.random.poisson(lambd_list[i],k))
print(P_come_lambda)
N_beginning=[[0 for i in range(k)] for j in range(len(lambd_list))] # количества абонентов в началах слотов для всех лямбд
N_final=[[0 for i in range(k)] for j in range(len(lambd_list))] # количества абонентов в концах слотов для всех лямбд
for j in range(len(lambd_list)):
for i in range(k): # заполнение количеств абонентов для одной лямбды
Rk=0 # количество передающих абонентов
if N_beginning[j][i]!=0:
Rk=np.random.binomial(N_beginning[j][i],1/N_beginning[j][i],1)
Indicator = 0
if(Rk==1):
Indicator=1
N_final[j][i] = N_beginning[j][i]+P_come_lambda[j][i]-Indicator
if(i
N_beginning[j][i+1]=N_final[j][i]
N_avg = [[] for i in range(len(lambd_list))] # массив средних значений количеств абонентов для каждой лямбды
for i in range(len(lambd_list)): # подсчёт средних количеств абонентов
N_avg[i] = sum(N_final[i])/k
print(N_avg[i])
k=10 # количество слотов
# матрица переходных состояний
P_come_lambda = [[[[] for j in range(k)] for i in range(k)] for l in range(len(lambd_list))] # количество абонентов, которое пришло в слоте k для каждой лямбды
for l in range(len(lambd_list)):
for i in range(k): #состояние, в которое осуществляется переход
for j in range(k): #состояние, из которого осуществляется переход
if i==0 and j<2: # для переходов в состояние П0
K=0
P_come_lambda[l][i][j]=poisson.pmf(k=K, mu=lambd_list[l])
elif j==0 or j==1: # для переходов из состояний П0 и П1
K=i
P_come_lambda[l][i][j]=lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K)
elif j==i+1: # для переходов из состояния i в состояние i-1
K=0
P_come_lambda[l][i][j] = lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K) * (math.factorial(j) / math.factorial(j-1)) * (1/j) *(1-1/j) ** (j-1)
elif j
K=i-j+1
P_come_lambda[l][i][j] = lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K) * (math.factorial(j) / math.factorial(j-1)) * (1/j) *(1-1/j) ** (j-1)
K=i-j # ни 1 абонент не передал сообщение
P_come_lambda[l][i][j]+=lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K) * (1 - math.factorial(j) / math.factorial(j-1) * (1/j) *(1-1/j) ** (j-1))
elif j==i: # для переходов из состояния i в состояние i
K=1 # 1 абонент передал сообщение, а 1 абонент пришёл
P_come_lambda[l][i][j] = lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K) * (math.factorial(j) / math.factorial(j-1)) * (1/j) *(1-1/j) ** (j-1)
K=0 # ни 1 абонент не передал сообщение и никто не пришёл
P_come_lambda[l][i][j] += lambd_list[l] ** (K) * math.e ** -lambd_list[l] / math.factorial(K) * (1 - math.factorial(j) / math.factorial(j-1) * (1/j) *(1-1/j) ** (j-1))
else:
P_come_lambda[l][i][j]=0
print(P_come_lambda[0])
for i in range(k):
print(P_come_lambda[0][i])
# для создания коэффициентов перед П отнимаем 1 от Пi,i
for l in range(len(lambd_list)): #для каждой лямбды
for i in range(k): #для каждого уравнения
for j in range(k): # номер слагаемого с П
if i==j:
P_come_lambda[l][i][j]-=1
print(P_come_lambda[0])
# замена последнего уравнения условием нормировки
for l in range(len(lambd_list)): #для каждой лямбды
for i in range(k): #для каждого уравнения
for j in range(k): # номер слагаемого с П
if i==k-1:
P_come_lambda[l][i][j]=1
# заполнение правой части системы уравнений
v_last=[[[] for i in range(k)] for l in range(len(lambd_list))]
for l in range(len(lambd_list)):
for i in range(k):
v_last[l][i]=0
if i==k-1:
v_last[l][i]=1
print(v_last[0])
final=[]
for l in range(len(lambd_list)):
final.append(np.linalg.solve(P_come_lambda[l],v_last[l]))
print(final[0])
#среднее количество абонентов
N_avg1 = [[] for l in range(len(lambd_list))]
for l in range(len(lambd_list)):
summ = 0
for j in range(k):
summ+=final[l][j]*j
N_avg1[l]=summ
print(N_avg1[l])
fig = plt.figure() # построения графика зависимости N от λ
ax = fig.add_subplot(111)
ax.set_ylim(0, 10) # ограничение среднего количества абонентов до 20
ax.set_ylabel("Среднее количество абонентов в системе, N")
ax.set_xlabel("Интенсивность входного потока (λ)")
ax.plot(lambd_list,N_avg1, label='Решением систем уравнений')
ax.plot(lambd_list,N_avg, label='Подсчет кол-ва абонентов в слоте k')
plt.legend()
plt.grid()
k=50
from scipy.stats import poisson
from scipy.stats import binom
P_come_lambda = [[[[] for j in range(k)] for i in range(k)] for l in range(len(lambd_list))] # количество абонентов, которое пришло в слоте k
for l in range(len(lambd_list)):
for i in range(k): #для каждого уравнения, состояние, в которое осуществляется переход
for j in range(k): # номер слагаемого с П; состояние, из которого осуществляется переход
if i==0 and j<2: #верно
K=0
P_come_lambda[l][i][j]=poisson.pmf(k=K, mu=lambd_list[l])
elif j==0 or j==1: #верно
K=i