Файл: Д. Ю. Соловьева М34 Математика. Методические рекомендации.docx
Добавлен: 28.03.2024
Просмотров: 89
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выполнение действий производится устно. Учащиеся при выполнении действий пользуются теми же приемами, какими они пользовались при изучении действий сложения и вычитания в пределах 100, т. е. раскладывают второй компонент действия (второе слагаемое или вычитаемое) на разрядные единицы и последовательно их складывают или вычитают из первого компонента.
Например:

5. Особые случаи сложения и вычитания. К ним относятся случаи, которые вызывают наибольшие трудности и в которых чаще всего допускаются ошибки. Учащихся больше всего затрудняют действия с нулем (нуль находится в середине числа или в конце). Случай с числами, содержащими нуль, не требует особых приемов. Но таких примеров надо решать больше, повторить перед решением таких примеров решение примеров на сложение и вычитание, когда компонентом действия является нуль (0 + 3, 5 + 0, 5 − 5):

Устные приемы вычислений требуют от учащихся постоянного анализа чисел по их десятичному составу, понимания места цифры в числе, понимания того, что действия можно производить только над одноименными разрядами. Не всем учащимся это становится понятным одновременно.
Перед выполнением действий необходимо добиваться от учащихся предварительного анализа десятичного состава чисел. Учитель чаще должен ставить вопросы: «С чего надо начинать сложение? Какие разряды складываем?»
В противном случае учащиеся допускают ошибки при вычислениях. Они складывают десятки с сотнями, а результат записывают либо в разряд сотен, либо в разряд десятков, например: 400 + 10 − 500, 30 + 400 = 70, 30 + 400 = 470, 30 + 400 = 340, 670 + 2 = 690, 670 − 3 = 640.
Эти ошибки свидетельствуют о непонимании позиционного значения цифр в числе, о неумении самостоятельно контролировать результаты действий. Учителю необходимо добиваться того, чтобы учащиеся проверяли выполнение действий, причем делали это не формально, а по существу. Нередко приходится наблюдать, что ученик якобы и сделал проверку, но выполнил ее формально. Он записал только обратное действие, а не решал, поэтому и не заметил допущенной ошибки, например: 490 − 280 = 110.
П р о в е р к а. 110 + 280 = 390.
Нередко можно столкнуться с непониманием учащимися (даже старших классов) сущности проверки. Проверка часто выполняется учениками только потому, что либо этого требует учитель, либо такое задание содержится в учебнике. Часто при выполнении проверки ученик получает несоответствие между полученным результатом и заданным примером, но это не служит ему поводом для исправления неверного ответа, например: 570 − 150 = 320.
П р о в е р к а. 320 + 150 = 470.
В данном случае проверка выступает как самостоятельное действие, никак не связанное с тем, которое ученик проверяет.
Учитель постоянно должен помнить об этих ошибках школьников и требовать от них ответа на вопросы: «Что показала проверка? Правильно ли решен пример? Как доказать, что действие выполнено верно?»
Осознанному выполнению устных вычислений, выработке обобщенных способов выполнения действий служит постоянное внимание к вопросам сравнения и сопоставления разных по трудности случаев сложения, вычитания. Важно научить учащихся видеть общее и особенное в тех примерах, которые они решают.
Например, сравнить примеры и объяснить их решение:

Полезно и составление учащимися примеров, аналогичных (похожих) данным, или примеров определенного вида: «Составьте пример, в котором надо сложить круглые сотни с единицами», «Составьте пример на вычитание, в котором уменьшаемое — трехзначное число, а вычитаемое — круглые десятки1». И т. д.
Для закрепления действий сложения и вычитания в пределах 1 000 приемами устных вычислений полезно решение примеров с неизвестными компонентами.
II. Сложение и вычитание с переходом через разряд.
Сложение и вычитание с переходом через разряд — это наиболее трудный материал. Поэтому учащиеся выполняют действия в столбик.
Сложение и вычитание в столбик производятся над каждым разрядом в отдельности и сводятся к сложению и вычитанию в пределах 20.
Но в этом случае возникают у умственно отсталых школьников трудности в записи чисел, т. е. в умении правильно подписать разряд под соответствующим разрядом.
Часто из-за неумения организовать внимание, из-за недостаточно четкого понимания позиционного значения цифр в числе, а то и из-за небрежности при записи цифр ученики сдвигают число, которое нужно прибавить или вычесть, влево или вправо и поэтому допускают ошибки в вычислениях. Особенно много ошибок учащиеся допускают при записи чисел в столбик, если действие производится над трехзначным и двузначным или однозначным числом. В этом случае десятки подписываются под сотнями, единицы — под сотнями или десятками. Это приводит к ошибкам в вычислениях. Например:
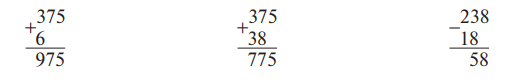
Наибольшие трудности вызывает действие вычитания. Ошибки в вычислениях носят различный характер. Причиной некоторых из них является слабое усвоение табличного сложения и вычитания в пределах 20.

Много ошибок допускается в результате того, что ученики забывают прибавить получившийся в уме десяток или сотню, а также забывают, что «занимали» сотню или десяток. Например:

Особенно трудны случаи, когда: 1) переход через разряд происходит в двух разрядах; 2) получается нуль в одном из разрядов; 3) содержится нуль в уменьшаемом; 4) в середине уменьшаемого стоит единица. Например:

Нередко при вычитании можно встретить и такую ошибку: вместо того чтобы занять единицу высшего разряда, раздробить ее, ученик начинает вычитать из большей цифры вычитаемого меньшую цифру соответствующего разряда уменьшаемого.
Например:

При этом рассуждение проводится так: «Из 5 единиц 8 единиц вычесть нельзя, вычитаем из 8 единиц 5, 7 десятков и 3 сотни сносим, разность 373».
Учитывая трудности изучения данной темы, необходимо повторить с учащимися сложение и вычитание с переходом через разряд в пределах 20 и 100, обратить внимание на решение примеров, в которых компонентом является нуль, или нуль получается в одном из разрядов суммы или разности (17 + 3, 25 + 15, 36 − 6, 36 − 27), или нуль содержится в одном из разрядов уменьшаемого или вычитаемого (60 − 45, 75 − 40).
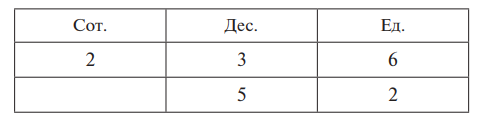
Учащимся, которые не могут усвоить запись примеров в столбик, можно разрешить записывать их в разрядную сетку.
При решении примеров на сложение и вычитание с переходом через разряд соблюдается такая последовательность:
1) Сложение и вычитание с переходом через разряд в одном разряде (единиц или десятков):
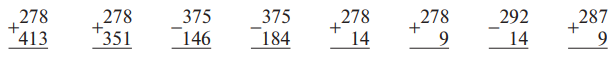
2) Сложение и вычитание с переходом через разряд в двух разрядах (единиц и десятков): 375 + 486, 375 − 186, 286 + 58, 375 − 86.
3) Особые случаи сложения и вычитания, когда в сумме или в разности получается один или два нуля, когда в уменьшаемом содержится один или два нуля, когда в уменьшаемом содержатся нуль и единица:
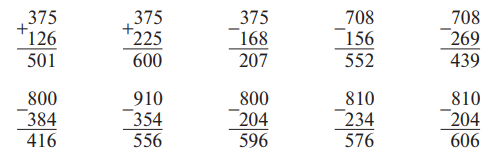
4) Вычитание трехзначных, двузначных и однозначных чисел из 1 000: 1 000 − 375, 1 000 − 75, 1 000 − 5.
При объяснении решения примеров с переходом через разряд, учитывая, что умственно отсталые школьники при сложении забывают прибавлять то число, которое надо запомнить, можно разрешать надписывать это число над соответствующим разрядом.
Например:

При вычитании же ставится точка над тем разрядом, из которого заняли единицу. Можно поставить и число 10, оно записывается над разрядом, к единицам которого этот десяток прибавляется.
Например:
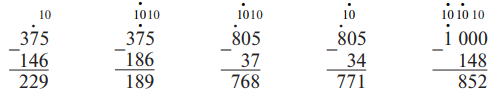
Особого внимания заслуживает решение примеров вида 800 − 236, 810 − 236, 810 − 206. Следует сопоставить сначала 1-й и 2-й, а потом 2-й и 3-й примеры, особенности их решения, объяснить, в чем их различие, почему получаются разные ответы.

При выполнении действий на сложение и вычитание в пределах 1 000 решаются примеры с тремя компонентами без скобок и с круглыми скобками: 375 + 36 + 124, 379 + (542 − 276), 910 − 375 − 264, 375 + 186 − 264, 1 000 − 565 + 136. Решаются также примеры на нахождение неизвестных компонентов действий. Проверка выполняется двумя действиями.
(Сложение проверяется сложением путем перестановки слагаемых и вычитанием. Вычитание проверяется сложением и вычитанием из уменьшаемого.)
Например:

УМНОЖЕНИЕ И ДЕЛЕНИЕ В ПРЕДЕЛАХ 1 000
Умножение и деление, так же как сложение и вычитание, могут производиться как устными, так и письменными приемами вычислений, записываться в строчку и столбик.
I. Устное умножение и деление в пределах 1 000.
1. Умножение и деление круглых сотен.
Умножение и деление круглых сотен основывается на знании учащимися нумерации, а также табличного умножения и деления. Поэтому, прежде чем знакомить учащихся с умножением и делением круглых сотен, необходимо повторить табличное умножение и деление, а также раздробление сотен в единицы и наоборот. Например: «Сколько единиц содержит 1 сотня? Сколько единиц в 5, 7, 10 сотнях? Сколько сотен составляют 300 единиц? 500 единиц?» И т. д. Объяснение умножения и деления должно сопровождаться операциями с наглядными пособиями и дидактическим материалом.
Приведем объяснение сначала умножения, а потом деления.
Например, 200 ⋅ 2. Рассуждаем так: «200 — это 2 сотни. Возьмем 2 сотни палочек и еще 2 сотни палочек. Будет 4 сотни, или 400. Запишем: 2 сот. ⋅ 2 = 4 сот. = 400, 200 ⋅ 2 = 400».
При делении 200 : 2 рассуждаем так: «200 — это 2 сотни. Возьмем 2 сотни палочек. Если разделить их на две равные части, то в каждой части получится по одной сотне, или по 100 единиц».
Запишем: 2 сот. : 2 = 1 сот. = 100, 200 : 2 = 100. Полезно сопоставить умножение и деление единиц, десятков и сотен:

Действия умножения и деления надо сопоставлять, проверяя каждое обратным действием: 400 ⋅ 2 = 800, 800 : 2 = 400.

