Файл: Д. Ю. Соловьева М34 Математика. Методические рекомендации.docx
Добавлен: 28.03.2024
Просмотров: 92
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для слабоуспевающих учащихся эта запись может оставаться единственной. Остальных учащихся по усмотрению учителя можно познакомить с более свернутой формой записи примеров такого вида, при которой умножение на нуль не производят, например 27 ⋅ 20:
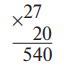
т. е. нуль второго множителя не подписывается под значащей цифрой первого множителя. Производится умножение первого множителя на 2, т. е. на число круглых десятков, а потом полученное произведение умножается на 10, т. е. приписывается к нему нуль справа.
Такая операция может быть понятна учащимся только в том случае, если будет проведена подготовительная работа. Перед умножением на круглые десятки устно следует повторить случаи умножения вида: 2 × 2 × 10, 2 × 20 и сравнить ответы этих примеров, объяснить, почему произведения равны. Учащиеся убеждаются, что второй множитель — круглый десяток (20, 30, ..., 90) — можно разложить на два множителя: на число десятков и 10. Сначала умножаем множитель на число десятков, а потом на 10. Затем надо порешать примеры на умножение двузначного числа на 10 (27 × 10, 38 × 10 и т. д.).
Решать примеры вида 27 × 20 следует устно. Объяснение их надо давать так, чтобы учащиеся поняли, почему умножаем на число десятков, а нуль приписываем к полученному произведению справа. Рассуждения проводятся так: «20 можно записать как произведение, т. е. 20 = 2 × 10, 27 ⋅ 20 = 27 ⋅ 2 × 10 = 54 ⋅ 10 = 540».
Запишем решение этого примера в столбик:
Сначала 27 умножим на 2, получим 54, а потом произведение 54 умножим на 10, т. е. припишем к нему нуль справа.
На первых порах учащиеся при решении этих примеров должны давать подробные объяснения. Затем рассуждения постепенно свертываются, но иногда следует задавать учащимся вопросы: «Почему при умножении на круглые десятки приписываем нуль справа? В виде произведения каких двух чисел можно записать второй множитель? На какое число сначала умножали первый множитель? На какое число потом умножали полученное произведение?» Эти вопросы позволяют учащимся более сознательно подходить к процессу выполнения умножения на круглые десятки. Кроме того, они готовят почву для сознательного выполнения умножения чисел на круглые сотни и тысячи.
Деление
Деление изучается в такой последовательности:
1) число сотен, десятков и единиц делится без остатка на делитель (369 : 3);
2) число сотен делится на делитель без остатка, а число десятков без остатка на делитель не делится (372 : 3);
3) число сотен не делится без остатка на делитель (570 : 3);
4) число сотен делимого меньше числа единиц делителя, в частном получается двузначное число (153 : 3);
5) особые случаи деления, когда в частном на конце или в середине получается нуль (720 : 3, 812 : 4, 820 : 4);
6) деление на круглые десятки.
Деление трехзначного числа на однозначное, когда сотни, десятки и единицы нацело делятся на делитель, учащиеся выполняют устно: 369 : 3 = 123. Однако на примере такого вида следует познакомить учащихся с новой формой записи деления в столбик. Рассуждения проводятся так: «Сначала записываем делимое. Знак деления обозначаем прямым углом, одна из сторон которого несколько продолжена вниз. Внутри угла записываем делитель. Деление начинаем с сотен (с высшего разряда). Частное от деления каждого разряда записываем под делителем. 3 сотни делим на 3, получаем 1 сотню, записываем ее в частное. Проверяем, все ли сотни разделили. 1 сотню умножаем на 3 и пишем под сотнями. Ставим знак «минус» (сотни вычитаем). Сносим 6 десятков и делим их на 3. И т. д. Частное 123».
Действие деления наиболее трудно для учащихся. Особенно трудны те случаи деления, в которых один или два разряда нацело не делятся на делитель, или случаи, в которых в частном получается нуль в середине. Дети нередко допускают ошибки, связанные с неправильным подбором числа в частном, — их не смущает, что при вычитании в остатке получается число, делящееся на делитель или больше делителя. Они не обращают внимание на то, что число, получившееся в частном, больше делимого.
Нередко в частном получается число, имеющее большее число знаков, чем делимое. Причинами таких ошибок опять являются неправильный выбор частного, получающийся больше делимого (или равный делителю) остаток.
Например:
Для того чтобы предотвратить подобные ошибки в вычислениях и помочь учащимся овладеть трудным для них действием деления, необходимо задолго до знакомства с приемами письменного деления провести подготовительную работу:
1. Постоянно, на каждом уроке повторять таблицу умножения и деления.
2. Решать примеры на деление с остатком: 15 : 2 = 7 (ост. 1), 21 : 4 = 5 (ост. 1), 61 : 6 = , 83 : 2 = и т. д., обращая внимание на то, что остаток должен быть всегда меньше делителя. Подбор цифр частного, например 24 : 5, следует производить постепенно: 24 на 5 не делится, делим 23, потом 22, 21, наконец, 20.
С самого начала знакомства с делением в столбик надо учить детей прикидке ответа, умению сразу определять, сколько цифр должно получиться в ответе.
Например, если делится трехзначное число на однозначное, а число сотен делимого больше делителя или равно ему, то в частном получатся сотни. Сотни стоят в числе на третьем месте. Значит, в ответе должно получиться трехзначное число. Можно рекомендовать в частном поставить сразу три точки, например:
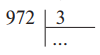
Если в трехзначном числе число сотен меньше делителя, то сотни надо раздробить в десятки, прибавить десятки делимого и начинать деление. В этом случае в частном получится двузначное число, так учащиеся как десятки стоят на втором месте. В частном
учащиеся ставят две точки. Предварительная прикидка количества цифр в числе предотвращает возможность пропуска нуля в частном или его недописывание. Особое внимание уделяется решению примеров, когда среди цифр частного получается нуль: 
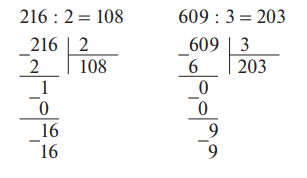
Когда учащиеся усвоят алгоритм деления, можно познакомить их с сокращенной записью:
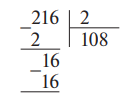
Действие деления проверяется умножением.
Решаются сложные примеры на все четыре арифметических действия и на порядок действий.
Деление на круглые десятки
Предварительным материалом к данной теме является решение примеров вида 80 : 20, 120 : 20, в которых учащиеся деление производят как деление по содержанию: 8 дес. : 2 дес. = 4 (раза), 12 дес. : 2 дес. = 6 (раз). На основании решения таких примеров учащиеся убеждаются, что если делимое и делитель оканчиваются нулями, то частное легче получить, если деление выполнять, не обращая внимания на нули, т. е. мысленно отбросить (120 : 20 = 6). При этом обращается внимание учащихся на то, что, отбрасывая нуль в делимом, мы его делим на 10.
Затем учащиеся знакомятся с делением трехзначного числа на двузначное, используя алгоритм письменного деления: делим 72 десятка на 3 десятка. От учащихся необходимо требовать проверки действия деления умножением.
Для закрепления действий, выработки прочных навыков вычислений и повторения теоретических знаний решаются примеры на нахождение неизвестных компонентов действия, порядок действий.
ИЗУЧЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
ОБУЧЕНИЕ НУМЕРАЦИИ МНОГОЗНАЧНЫХ ЧИСЕЛ
При изучении данного раздела можно выделить следующие ступени:
1) знакомство с новыми счетными и разрядными единицами: единицей тысяч, десятком тысяч, сотней тысяч, единицей миллионов;
2) счет до 1 млн уже известными счетными единицами и новыми: десятками тысяч и сотнями тысяч;
3) выработка прочных навыков в записи чисел до 1 млн;
4) повторение класса единиц и знакомство с классом тысяч (1—2 классы); 32
5) анализ многозначных чисел по десятичному составу — выделение в числе классов и разрядов, составление числа по данным классам и разрядам.
Учащимся необходимо показать, где в практике, в жизни используются те многозначные числа, которые они изучают на уроках в школе.
Нумерация многозначных чисел усваивается учащимися с большим трудом. Эти трудности связаны в первую очередь с тем, что многозначное число трудно конкретизировать. Наглядные пособия, которые используются при изучении данной темы, — абак, счеты, таблица разрядов и классов. Таблицы соотношения мер длины и мер массы являются условными пособиями. Они скорее конкретизируют не число, а десятичную систему счисления. Обобщенные понятия, которые используются для усвоения как устной, так и письменной нумерации, носят также условный и отвлеченный характер. К ним относятся понятия разряда, класса, поместного значения цифры в числе и др.
Учащиеся испытывают затруднения в счете как простыми единицами, так и другими единицами счета (десятками, сотнями, единицами тысяч и др.). Когда надо сделать переход к новому разряду или классу (1 299—1300, 2 999—3 000), ученик считает: две тысячи девятьсот девяносто десять и т. д. Как и раньше, при изучении чисел предыдущих концентров наибольшие затруднения вызывает счет в обратном порядке и счет равными числовыми группами (по 25, 50, 200, 250, 500).
Наблюдаются также трудности при чтении многозначных чисел. На первых порах ученики не выделяют при чтении класса тысяч (например, число 4 231 читают как 423 1 или 42, 31, не учитывают нулей при чтении чисел (например, число 5 620 читают как 562, 3085 читают как 385 или 3, 0, 85).
Не только чтение, но и выработка умений и навыков при письме многозначных чисел требует от учащихся значительных усилий, большого количества тренировочных упражнений. Учащиеся переставляют цифры местами, значит, испытывают трудности в усвоении позиционного значения цифр в числе, пропускают нули или вписывают лишние (например, число 308 576 записывают как 38 576, число 38 000 записывают как 380 000, число 80 050 записывают как 80 500 и т. д.).
Нечеткое представление о разрядах, классах нередко затрудняет сравнение соседних разрядов и классов (например, 2, 20, 200, 2 000; 5 и 5 тысяч; 60 и 60 тысяч), нахождение наибольшего и наименьшего чисел каждого разряда.
Причем трудности, возникающие у учащихся при изучении темы «Нумерация многозначных чисел», неоднородны. Одни учащиеся довольно быстро усваивают устную нумерацию (счет и анализ чисел), но долго не могут постичь письменную нумерацию. Для других оказывается проще усвоение письменной нумерации, а последовательность счета, десятичный анализ чисел усваиваются медленнее, с большим трудом.
Изучение нумерации многозначных чисел не должно ограничиваться только теми уроками, которые отводятся на первоначальное знакомство с этой темой. Упражнения на закрепление устной и письменной нумерации должны быть неотъемлемой частью почти каждого урока математики. Их следует включать в устный счет, арифметические диктанты. От сознательного усвоения нумерации зависит успех овладения арифметическими действиями.
В данном пособии предлагается методика изучения многозначных чисел до 1 000 000, с учетом разной последовательности при изучении нумерации многозначных чисел.
I в а р и а н т. Методика изучения. Последовательность:
1. Повторение нумерации в пределах 10, 100, 1 000 (особое внимание обращается на образование новой счетной единицы из 10 предшествующих).
2. Нумерация целых тысяч до 10 000 (счет единицами тысяч до 10 000 в прямом и обратном порядке). Обозначение круглых тысяч на письме.
3. Нумерация четырехзначных чисел:
а) счет сотнями, десятками, единицами до 10 000;
б) образование и запись полных и неполных четырехзначных чисел;
в) анализ чисел;
г) округление числа до указанного разряда.
В такой же последовательности изучается нумерация в пределах 100 000 и 1 000 000.