ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
По предмету «МАТЕМАТИЧЕСКИЕ МЕТОДЫ»
-
Основные понятия: решение, множество возможных решений, оптимальное решение, показатель эффективности. -
Математические модели, основные принципы построения моделей, аналитические и статические модели. -
Классификация задач, возникающих в практической деятельности и подходы к их решению: прямые и обратные задачи. -
Классификация задач, возникающих в практической деятельности и подходы к их решению: детерминированные задачи и задачи в условиях неопределенности. -
Классификация задач, возникающих в практической деятельности и подходы к их решению: однокритериальные и многокритериальные задачи. -
Методы решения многокритериальных задач (выделение множества Парето, линейная свертка, наложение ограничений на показатели эффективности, метод последовательных уступок). -
Общий вид задач линейного программирования (ЛП). -
Основная задача линейного программирования (ОЗЛП) и сведение произвольной задачи линейного программирования к основной задаче линейного программирования. -
Симплекс–метод при решении ОЗЛП. -
Транспортная задача. -
Методы нахождения начального решения транспортной задачи (дописать). -
Метод потенциалов в решении транспортной задачи. -
Общий вид задач нелинейного программирования. Графический метод решения задач нелинейного программирования. -
Метод множителей Лагранжа для решения задач нелинейного программирования. -
Основные понятия динамического программирования: шаговое управление, управление операцией в целом, оптимальное управление, выигрыш на данном шаге, выигрыш за всю операцию, аддитивный критерий, мультипликативный критерий. -
Идея метода динамического программирования. Простейшие задачи, решаемые методом динамического программирования. -
Определение графа и его основные характеристики. Вершины и ребра. Графическая интерпретация графа. Смежность и инцидентность. Локальная степень. Подграф. Полный подграф. -
Определение графа. Матрицы смежностей и инциденций. Методы хранения графов в памяти ЭВМ. -
Путь в графе и связные компоненты графа. Цепи, простые цепи, циклы, простые циклы. Операции удаления вершины, удаления ребра. Дерево и его особенности. -
Определение паросочетаний в графе и их разновидностей. Двудольные графы и алгоритм выбора наибольшего паросочетания в двудольном графе. -
Планарные и плоские графы. Формулировки теоремы Эйлера о соотношении чисел граней, ребер и вершин плоского графа. -
Методы хранения графов в памяти ЭВМ. Взвешенный граф. Кратчайшие пути во взвешенном графе и алгоритм Форда построения кратчайших маршрутов. -
Сети и потоки в сетях. Задача о максимальном потоке и алгоритм Форда–Фалкерсона. -
Ориентированный граф и его графическая интерпретация. Локальные степени. Матрица смежностей. Ориентированные пути и связность в ориентированном графе. -
Задача о коммивояжере. -
Понятие системы массового обслуживания, классификация систем массового обслуживания. Простейшие системы массового обслуживания и их параметры. -
Основные понятия теории марковских процессов: случайный процесс, марковский процесс, граф состояний, поток событий, вероятность состояния, уравнения Колмогорова, финальные вероятности состояний. -
Предмет и задачи теории игр. Основные понятия теории игр: игра, игроки, партия, выигрыш, проигрыш, ход, личные и случайные ходы, стратегические игры, стратегия, оптимальная стратегия.-
Антагонистические матричные игры: чистые и смешанные стратегии. Методы решения конечных игр: сведение игры mxn к задаче линейного программирования. -
Назначение и области применения сетевого планирования и управления. Сетевая модель и её основные элементы. Порядок и правила построения сетевых графиков.
-
1. Основные понятия: решение, множество возможных решений, оптимальное решение, показатель эффективности.
Исследов-е операций – прим-е мат., кол-венных методов д/обоснования решений во всех обл-тях целенаправленной человеч.деят-ти. Операция – любое управляемое мероприятие, направленное на достиж-е цели. Рез-т операции зависит от способа ее проведения, орг-ции (от выбора некоторых пар-ров). Всякий опр.выбор пар-ров наз-ся решением. Те пар-ры, совок-ть ктр образует решение, наз-ся эл-тами решения. Оптимальными считаются те решения, ктр по тем или иным соображ-ям предпочтительнее др. Поэтому осн.задачей исследов-я операций явл-ся предварительное кол-венное обоснование опт.решений. #Д/реализации опр.партий сезон.товаров создается сеть временных торговых точек. Т.е. требуется выбрать пар-ры сети: число точек, их размещ-е, кол-во персонала так, чтобы обеспечить мах экономич.эф-ть распродажи. Чтобы сравнивать между собой по эф-ти разные решения, нужно иметь какой-то кол-венный критерий – показ-ль эф-ти (целевая f-я). Этот показ-ль выбир-ся так, чтобы он отражал целевую направлен-ть операции. «Лучшим» будет считаться то решение, ктр в мах степени способствует достижению поставлен.цели. Иногда выполнение операции сопровожд-ся действием случ.факторов («капризы» погоды, колебания спроса и предлож-я). В таких случаях обычно в кач-ве показ-ля эф-ти берется не сама величина, ктр хотелось бы мах-ровать (min-ровать), а ее среднее знач-е (мат.ожидание). В некотор.случаях бывает, что операция, сопровождаемая случ.факторами, преследует какую-то опр.цель, ктр может быть только достигнута полностью или совсем не достигнута, и никакие промежуточ.рез-ты нас не интересуют. Тогда в кач-ве показ-ля эф-ти выбир-ся вер-ть достиж-я этой цели.
2. Математ-е модели, осн-е принципы постр-я моделей, аналит-е и статич-е модели.
Д/прим-я кол-венных методов исследования в любой обл-ти всегда требуется какая-то мат.модель. При построении модели реал.явление неизбежно упрощ-ся и описыв-ся с помощью того или другого мат.аппарата. Чем удачнее будет подобрана мат.модель, чем лучше она будет отражать хар-ные черты явления, тем успешнее будет исследов-е и полезнее вытекающие из него рекомендации. Общих способов построения мат.моделей не сущ-ет. В кажд.конкрет.случае модель выбир-ся, исходя из вида операции, ее целевой направлен-ти. Необх-мо также в кажд.конкрет.случае соразмерять точность и подроб-ть модели: а)с той точностью, с ктр нам нужно знать решение; б)с той i-цией, ктр мы располагаем или можем приобрести. В исследовании операций прим-ся как аналитические, так и статистические модели, каждая из ктр имеет свои недостатки и преимущ-ва. Аналитич.модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато рез-ты расчета по ним легче обозримы, отчетливее отражают присущие явлению закономер-ти. Аналит.модели больше приспособлены д/поиска опт.решений. Статистич.модели более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое число факторов. Недостатки: громоздкоть, плохая обозримость, большой расход машин.времени, крайняя трудность поиска опт.решений, ктр приходится искать путем догадок и проб.
3. Классиф-я задач, возник-х в практ-й деятел-ти и подходы к их решению: прямые и обрат-е з-и.
Задачи исследования операций делятся на 2категории: прямые и обратные. Прямые задачи отвечают на вопрос: что будет, если в заданных условиях мы примем какое-то решение хХ? В частности, чему будет =, при данном решении х, выбранных показ-ль эф-ти W? Д/решения такой задачи строится мат.модель, позволяющая выразить 1 или неск-ко показ-лей эф-ти через заданные условия и эл-ты решения. Обратные задачи отвечают на вопрос: как выбрать решение х д/того, чтобы показ-ль эф-ти W обратился в мах? Если число возможных вариантов реш-я, образ-х множ-во Х, невелико, то можно попросту вычислить величину W д/каждого из них, сравнить между собой полученные знач-я и непоср-венно указать 1 или неск-ко опт.вариантов, д/ктр W достигает мах. Такой способ нахожд-я опт.решения наз-ся «простым перебором». Однако, когда число возможных вариантов решения, образующих множ-во Х, велико, поиск среди них оптимального «вслепую», прост.перебором, затруднителен, а зачастую практически невозможен. В этих случаях прим-ся методы «направленного перебора», обладающие той общей особен-тью, что опт.решение нах-ся рядом последовательных «попыток» или «приближений», из ктр каждое последующее приближает нас к искомому оптимальному.
5. Классиф-я задач, возникающих в практической деят-ти и подходы к их решению: однокритер-е и многокритер-е задачи.
Однокритериальный подход- когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум(минимум) один-единственный показатель W #собираешься на отдых не знаешь какая погода будет точно(нужно решить какую одежду взять- один критерий). Рассм-м пример такой задачи. Орган-ся оборона важного объекта от возд-х налетов. В нашем распоряж-и - какие-то средства противовозд-й обороны, кот-е надо разумным образом разместить вокруг объекта, организовать их взаимодействие, распределить между ними цели, назначить боезапас н т. д. главная задача операции - не допустить к объекту ни одного самолета, а естеств-й показатель эффект-ти - вероятность Wтого, что ни один самолет не прорвется к объекту. М - среднее число пораженных целей, кот-й нам тоже хотелось бы максимизировать; П - еще один крит-й, кот-й хотелось бы минимиз-ть. Несмотря на ряд существенных трудностей, связанных с неопределен-ю, мы до сих пор рассматр-ли только самые простые случаи, когда ясен крит-й, по кот-му произв-ся оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показ-ль W. К сожалению, на практике такие задачи, где критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто - преимущественно при рассм-и небольших по масштабу и скромных по значению меропр-и. А когда идет речь о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффект-ть, как правило, не может быть полностью охарактеризована с помощью одного единственного показ-ля эффект-ти W. На помощь ему приходится привлекать другие, дополнит-е. Такие задачи исследования операций наз-тся многокритериальными. Итак, типичной для крупномасшт-й задачи исследования опер-й является многокритер-е - наличие ряда количеств-х показат-й, один из кот-х желательно обратить в максимум, другие – в минимум.
7. Общий вид задач лин-го программир-я (ЛП).
Они явл-ся наиболее простыми среди задач исследования операций, где выбор показ-лей эф-ти (целевой f-ции) W достаточно явно диктуется целевой направлен-тью задачи, а ее усл-я – известны заранее (детерминирован.случай). W=W (,x), где - факторы, налагаемые на эл-ты решения х некоторые огранич-я. Wmax (min). Трудности, возникающие при решении задач мат.программир-я, зависят: ф)от вида f-ной завис-ти, связывающей W с эл-тами решения; б)от «размер-ти» задачи, т.е.от кол-ва эл-тов решения х1, х2, …, хn; в)от вида и кол-ва огранич-й, наложенных на эл-ты решения. Д/задач ЛП хар-но: 1)показ-ль эф-ти (цел.f-я) W линейно зависит от эл-тов решения х1, х2, …, хn; 2)огранич-я, налагаемые на эл-ты решения, имеют вид лин.нерав-в или ур-й относ-но х1, х2, …, хn. К задачам ЛП относ-ся задачи распред-я ресурсов, планирования произв-ва, орг-ции работы транспорта.
4. Классиф-я задач, возник-х в практ-й деятельности и подходы к их решению: детерминир-е задачи и задачи в условиях неопредел-ти.
Обратные задачи отвечают на вопрос: как выбрать решение х д/того, чтобы показ-ль эф-ти W обратился в мах? Если число возможных вариантов решения, образующих множ-во Х, невелико, то можно попросту вычислить величину W д/каждого из них, сравнить между собой получ-е знач-я и непоср-венно указать 1 или неск-ко опт.вариантов, д/ктр W достигает мах. Такой способ нахожд-я опт.решения наз-ся «простым перебором». Сейчас мы ограничимся постановкой задачи оптимизации решения (обратной задачи исследования операций) в самой общей форме. Пусть имеется некот-я операция Q, , па успех кот-й мы можем в какой-то мере влиять, выбирая тем или другим способом реш-е х (напомним, что х — не число, а целая группа параметров). Пусть эффектив-ть операции характер-ся одним показат-м W max. Возьмем самый простой, так назыв-й «детерминированный» случай, когда все условия операции полностью известны заранее, т. е. не содержат неопредел-ти. Тогда все факторы, от которых зависит успех опер-и, делятся на две группы: 1) заданные, заранее известные факторы (условия выпол-я опер-и), кот-е мы д/краткости обозначим одной буквой а; 2) зависящие от нас элем-ты реш-я, образующие в своей совок-ти реш-е х. Заметим, что первая группа факт-в содержит, в частности, и огранич-я, налаг-е на реш-е, т. е. определяет область возм-х решений X. Показ-ль эффект-ти Wзависит от обеих групп факторов W=W(,x), как х, так и а в общем случае — не числа, а совокупности чисел (векторы), функции в т. д. В числе заданных условий ее обычно присутствуют огран-я, налагаемые на эл-ты реш-я, имеющие вид равенств или неравенств. При заданном комплексе условий а. найти такое решение х = х*, которое обращает показатель эффект-сти W в максимум. Эта задача принадлежит к классу так называемых «вариационных задач», хорошо разработ-х в математике. Самые простые аз таких задач («задачи на максимум и минимум») знакомы каждому инженеру. Чтобы найти максимум или минимум (короче, «экстремум») ф-я многих аргументов, надо продифференцировать ее по всем аргументам (в данной случае — элементам решения), приравнять производные нулю и решить полученную сис-му уравн-й. Метод поиска экстремума и связанного с ним оптим-го решения х* должен всегда выбираться исходя из особен-й функции Wи вида ограни-й, накладыв-х на реш-е. #, если фун-я Wлинейно зависит от элем-в реш-я X1, Х2, ..., а огран-я, налагаемые на X1, Х2,.. имеют вид линейных равенств или неравенств, возникает ставшая классич-й задача лин-го программир-я, кот-я решается сравн-но простыми, а главное, станд-ми методами. Д/оптимизации управл-я многоэтапными опер-ми примен-ся метод динамического програм-я . Наконец, сущ-ет целый набор числ-х методов отыскания экстремумов, специально приспособленных для реализации на ЭВМ; некот-е из них включают элемент «случайного поиска», который д/многомерных задач нередко оказывается эффективнее упорядоченного перебора. Т. О., задача нахождения оптимал-го реш-я в простейшем, детерминированном случае есть чисто математ-я задача, принадл-я к классу вариационных (при отсутствии или наличия ограничений), кот-я может представить вычислит-е, но не принцип-е трудности. В предыдущем мы рассмотрели обратную задачу исследования опер-й в детерминированном случае, когда показатель эффективности Wзависит только от двух групп факторов: заданных, заранее известных а и элементов решения х. Реальные задачи исслед-я опер-й чаще всего содержат помимо этих двух групп еще одну — неизвес-е факторы, кот-е в совок-ти мы обозначим одной буквой . Итак, показатель эффект-ти Wзависит от всех трех групп факторов: W=W(, х, ). Так как величина Wзависит от неизв-х факторов, то даже при заданных а и х она уже не может быть выч-на, остается неопред-й. Задача поиска оптимал-го реш-я тоже теряет определ-ть. # 1: планируется ассортимент товаров на распродажи на ярмарке. Желат-но было бы максимиз-ть прибыль. Однако заранее неизвестно ни кол-во покуп-й, кот-е придут на ярмарку, ни потр-ти каждого покуп-ля. # 2: Проект-ся сис-ма сооруж-й, оберегающих район от паводков. Ни моменты их наступления, ни размеры заранее не известны. # 3: разрабатывается план вооружения страны на несколько лет вперед, но неизвестны ни конкретный противник, ни вооружения, кот-м он будет располагаться. Д/того, чтобы такие решения принимать современная наука располагает рядом приемов. Каким из них воспольз-ся — зависит от того, какова природа неизвестных факторов , откуда они возникают и кем контрол-ся. Классифицировать неопредел-ти по «родам» и «сортам». «Доброкачественный» вид неопредел-ти - это случай, когда неизв-е факторы предст-т собой обычные объекты изучения теории вероятн-й — случайные велич-ны (или случайные фун-и), статистические характер-ки кот-х нам известны или в принципе могут быть получены к нужному сроку. Такие задачи исслед-я операций мы будем называть стохастическими задачами, а присущую им неопредел-ть — стохастической неопределен-ю. Возьмем самый грубый пример: пусть мы ведем обстрел какой-то цели, стремясь во что бы то ни стало попасть в нее. Произв-ся несколько выстрелов. Давайте заменим все случайные координаты точек попадания их математическим ожиданием — центром цели. Получится, что любой выстрел с гарантией попадет в цель, что заведомо неверно. Гораздо хуже обстоит дело, когда неизвестные факторы не могут быть изучены и описаны статистич-ми методами. Это бывает в 2 случаях: либо распред-е вероятн-й д/параме-в в принципе сущ-ет, но к моменту принятия решения не может быть получена. Либо распределение вероятн-й вообще не сущ-т. Пример ситуации типа а): проектируется информ-но вычислит-я система (ИВС), предназначенная д/обслужив-я каких-то случайных потоков требов-й (запросов). Вероятн-е характеристики этих потоков требов-й в принципе могли бы быть получены из статистики, если бы данная ИВС (или аналогичная ей) уже существ-ла и функционир-ла достаточно долгое время. Но к моменту создания проекта такой инф-и нет.
6. Методы решения многокритер-х задач.
Парето - Пусть в составе множ-ва возможных решений есть два решения х1и х2 такие, что все критерии W1, W2,…, Wк для первого реш-я больше или равны соответствующим критериям для второго реш-я, причем хотя бы один из них действит-но больше. Очевидно что в составе множества Х нет смысла сохранять решение х2, оно вытесняется решением х1. Выбросим решение х2, как не конкурентно спос-е и перейдем к сравнению других по всем критериям. В результате отбрасыв-ся не выгодные решения, множество Х сильно уменьшается. В нем сохраняются только эффективные(паретовские) реш-я. Линейная свертка – здесь участвуют человек и ПК. Указывается вес события:а1,а2,…,а3.Машина производит расчеты и выдает показатели эффективности(как бы в ряд): W1, W2… Wn, а человек может критически оценить ситуацию и внести измен-я в весовые коэфф-ты(или иные параметры управляющего алгоритма). В конечном итоге решение все равно принимает человек. наложение ограничений на показ-ли эффективности – надо выделить один(главный) показатель W1 и стремиться его обратить в максимум, а на все остальные W2, W3, ....( чтобы прибыль была максим-я, план по ассортименту выполнен, а себестоимость прод-и не выше заданной). При таком подходе все показ-ли, кроме одного – главного перев-ся в разряд заданных условий а(альфа). метод последовательных уступок – Предположим что показатели W1, W2… Wn, расположены в порядке убывающей важности. Сначала ищется решение, обращающее в максимум первый(важнейший) показатель W1= W1*. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая уступка и ΔW1, которую мы согласны сделать для того чтобы максим-вать второй показатель W2. Наложим на показатель W1 ограничение: чтобы он был меньше, чем W1*- ΔW1, и при этом ограничении ищем решение, обращающее в максимум W2. Далее снова назначаем уступку в W2, ценой которой можно максимизировать W3, и т.д. Такой способ построения компромиссного хорош тем, что здесь сразу видно, ценой какой уступки, в одном показателе приобретается выигрыш в другом и какова величина этого выигрыша.
8. Осн-я задача лин-го программир-я (ОЗЛП) и сведение произв-й задачи лин-го программир-я к осн-й задаче лин-го прогр-я.
Любую задачу ЛП можно свести к стандарт.форме (ОЗЛП), ктр формулир-ся так: найти неотриц.знач-я переменных х1, х2, …, хn, ктр удовлетворяли бы условиям-рав-вам
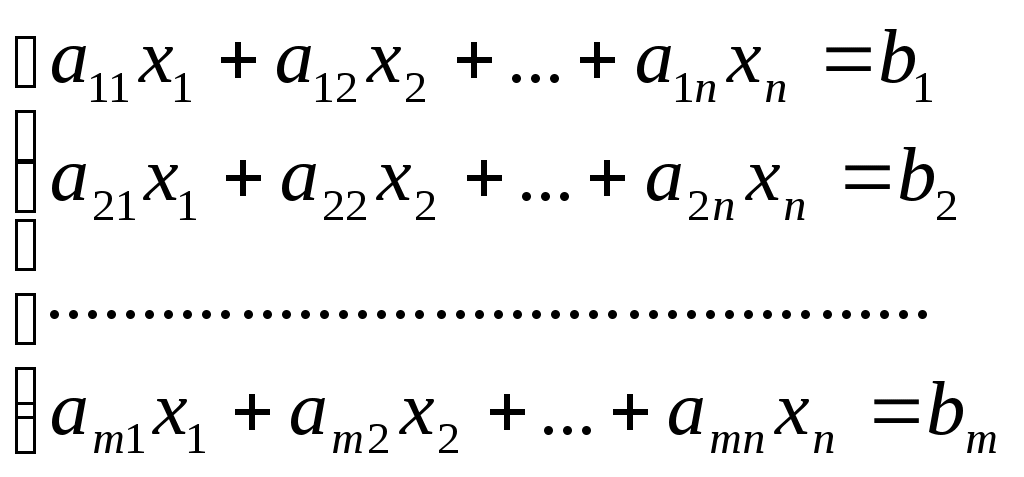
и обращали бы в мах лин.f-ю этих переменных:
Назовем допустимым решением ОЗЛП всякую совок-ть неотриц.знач-й х1, х2, …, хn, удовлетворяющую условиям системы. Оптимальным назовем то из допустимых решений, ктр обращает в мах f-ю L. Требуется найти оптим.решение. Задачи ЛП сводятся к ОЗЛП, где необх-мо найти неотриц.знач-я пер-ных х1, х2, …, хn, удовлетворяющие сис-ме m-лин.нерав-в и ур-й, и обращающие в max (min) лин.f-ю этих пер-ных. F=c1x1+c2x2+…+cnxn→max (min). Назовем допустимым решением ОЗЛП всякую совок-ть неотриц.знач-й х1, х2, …, хn, удовлетвор.сис-ме огранич-й. Оптимальным назовем то из допустим.реш-й, ктр обращает в max(min) цел.f-ю. Рассмотрим задачу ЛП с 2мя пер-ными (n=2). Пусть геом.изображ-ем сис-мы огранич-й явл-ся многоуг-к. Необх-мо среди точек этого мног-ка найти такую точку (вершину), в ктр лин.f-я принимает max (min) знач-е. Рассмотрим так наз-мую линию уровня лин.f-и F, т.е. линию, вдоль ктр эта f-я принимает одно и тоже фиксирован.знач-е а, т.е. с1х1+с2х2=а. На мног-ке реш-й следует найти точку, через ктр проходит линия уровня f-и F с наибольшим (если f-я max-ется) или наим.(если f-я min-ется) уровнем. Ур-е линии уровня f-и есть ур-е прямой линии. При различ.уровнях а линии уровня //, т.к. их угловые коэф-ты опр-ся только соотнош-ем между коэф-тами с1 и с2, и след-но, =. Т.о., линии уровня f-и F – это своеобразные параллели, расположенные обычно под углом к осям корд-т. Важн.св-во линии уровня лин.f-и состоит в том, что при // смещении линии в одну сторону уровень только возрастает, а при смещ-и в др.сторону – только убывает.
9. Симплекс–метод при решении ОЗЛП.
Симплекс-метод явл-ся одним из способов решения ЗЛП. Идея последоват.улучшения решения легла в основу универсал.метода решения ЗЛП – с-м. Геометрич.смысл с-м состоит в последоват.переходе от одной вершины (первоначальной) многогранника огранич-й к соседней, в ктр лин.f-я принимает лучшее (не худшее) знач-е (по отношению к цели задачи) до тех пор, пока не будет найдено оптим.реш-е – вершина, где достиг-ся оптим.знач-е f-и цели (если задача имеет конечный оптимум). С-м – это вычислит.процедура, основанная на принципе последоват.улучшения решений при переходе от одной базисной точки (базисного решения) к др. При этом знач-е цел.f-и улучшается. Базисным реш-ем явл-ся одно из допустимых реш-й, нах-щихся в вершинах области допустимых знач-й. Проверяя на оптим-ть вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан с-м. С-м может быть найден на мах и min.
1.MAX. (Задача об использ-и ресурсов): имеются 2вида продукции P1 и P2, использ-ся 4вида ресурсов S1, S2, S3, S4. Необх-мо составить такой план произв-ва продукции, при ктр прибыль от ее реализации будет мах. 1)Необх-мо из сис-мы огранич-й, ктр выглядит в виде сис-мы нерав-в, сделать сис-му ур-ий (если «», то осн.пер-ные со знаком +, если «», то -). Д/этого придется ввести дополнит.неотриц.переменные. Опр-м, какие из переменных явл-ся осн., а какие – неосн. Пр-ло: в кач-ве осн.пер-ных на I шаге следует выбрать (если возможно) такие m-пер-ных, каждая из ктр входит только в 1 из m-ур-ий сис-мы огранич-й, при этом нет таких ур-ий сис-мы, в ктр не входит ни одна из этих пер-ных. Далее выражаем осн.пер-ные через неосн. Положив, неосн.пер-ные = 0, получим I базисное реш-е. 2)Составим сим.таблицу: а)исх.расширен.сис-му (в ктр выражали осн.пер-ные через неосн.) заносим в I сим.таблицу. Послед.строка таблицы, в ктр приведено ур-ие д/лин.f-и цели, наз-ся оценочной. В ней указыв-ся коэф-ты цел.f-и с противополож.знаком. В лев.столбце таблицы записываем осн.пер-ные (базис), в I строке таблицы – все пер-ные (отмечая при этом осн.), во II столбце – свобод.члены расширен.сис-мы
Последний столбец – д/оц.отнош-й, необх-мых при расчете наибольшего знач-я пер-ной. В рабоч.часть таблицы занесены коэф-ты
таблица преобраз-ся по опр.правилам. б)Проверяем выполн-е критерия оптим-ти. При реш-и задачи на мах – наличие в послед.строке отриц.коэф-тов. Если таких коэф-тов нет, то реш-е оптимально, т.е. достигнут мах. При этом
столбец). Осн.пер-ные = 0, т.е. получено оптим.реш-е. Иначе, переходим к след.шагу. в)Если критерий оптим-ти не выполнен, то наибольший по модулю отриц.коэф-т в послед.строке таблицы опр-ет разрешающий столбец S. Составляем оц.отнош-я
кажд.строки по след.правилам: а)


