ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
аj (или чисел неориентированных ребер, соединяющих эти вершины)
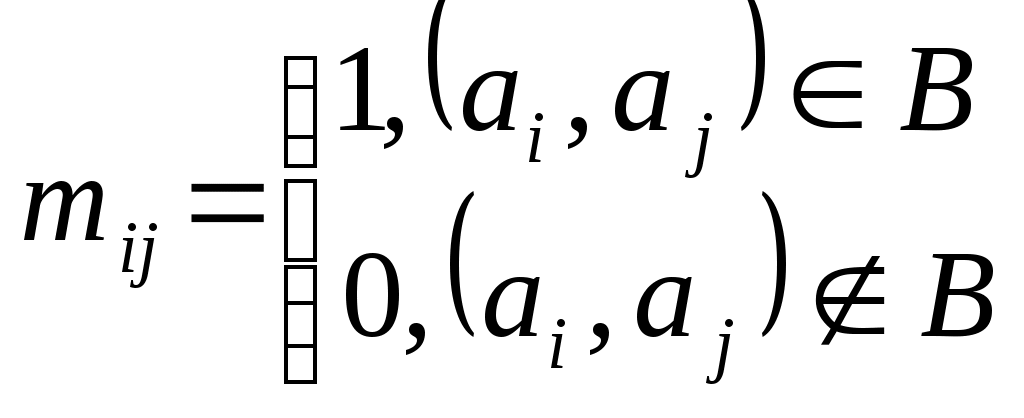
Эта матрица симметричная. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4).
Другой вариант матричного представления — матрица инциденций является классическим способом в теории графов. Это не экономичный способ задания.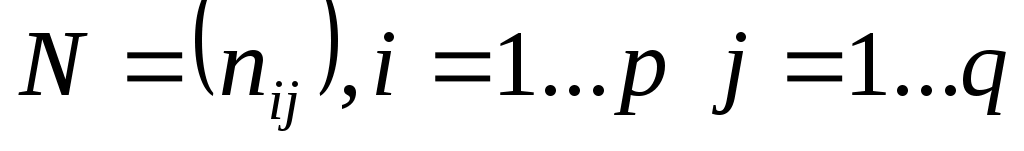
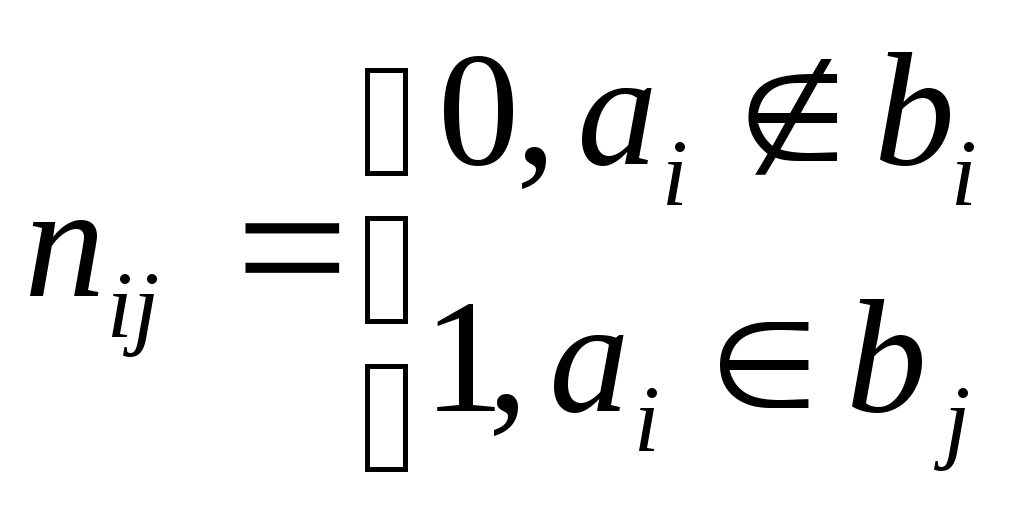
Данная матрица зависит от того как занумерованы ребра. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4). i=5; j=6.
В данной матрицы в каждом столбце две 1, т.к. одному ребру всегда инцидентно только две вершины. Если в графе все вершины имеют степень 0, то матрица инцидентности не сущ-ет. В ЭВМ удобно представлять графы в виде матриц смежнотей: если направление ребра противоположено, то в матрицу составим (-1).
19. Путь в графе и связные комп-ты графа. Цепи, простые цепи, циклы, простые циклы. Операции удал-я вершины, уд-я ребра. Дерево и его особ-ти.
Графом называется пара множеств Г=[А,В], где А – любое непустое множество, а В – множество, которое является подмножеством множества V(A). Элементы из А называются вершинами графа, а элементы из В – его ребрами. Например, А={1,2,3,4,5}, В={(1,2),(2,3),(3,4),(1,5),(1,4),(3,1)}. Неупорядоченная пара вершин – ребро, а упорядоченная пара – дуга. Путем в графе Г называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным. Подграф содержит подмножество вершин графа и все соединяющие их рёбра. Компонента связности – максимально связанный подграф. Путь без повтор-ся ребер наз-ся цепью, а цепь без повтор-ся вершин называется простой. Цепь, в кот-й совпадают концевые вершины наз-ся циклом, а цикл, в кто-м нет повто-х вершин, кроме концевых, наз-ся простым. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги – ориентированным или орграфом. Граф называется петлей, если его начало и конец совпадают. Удаление ребра. Г=[А,В] и a А, b В. Удалить ребро b это значит построить новый граф Г`=[А` ,В`],
в кот-м А`=А, В`=В\b





Удаление вершин. Г=[А,В] и a А, чтобы удалить вершину а из Г=[А,В] нужно, построить граф новый Г`=[А` ,В`], в кот-м А`=А\{a}, В` получится из В удал-е все ребра. (а будет на пересечении)
Д
 ерево
ерево
– это граф без циклов. Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины. (первый явл., а второй не явл.). Если Г=[А,В] явл. Деревом и число его вершин = р, то о числе ребер можно сказать совершенно опред-но: в дереве имеется еще одна особенность любые две вершины в дереве связаны и при этом единственной простой цепью.
29. Сети и потоки в сетях. Задача о максимальном потоке и алгоритм Форда–Фалкерсона.
Пусть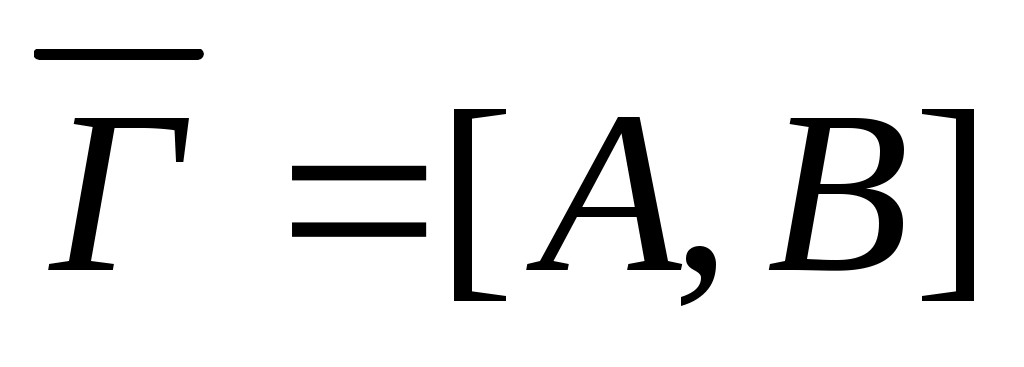 - некоторый орграф и f: B→R – вещ-но-значная f-я на мн-ве ребер, тогда пара
- некоторый орграф и f: B→R – вещ-но-значная f-я на мн-ве ребер, тогда пара 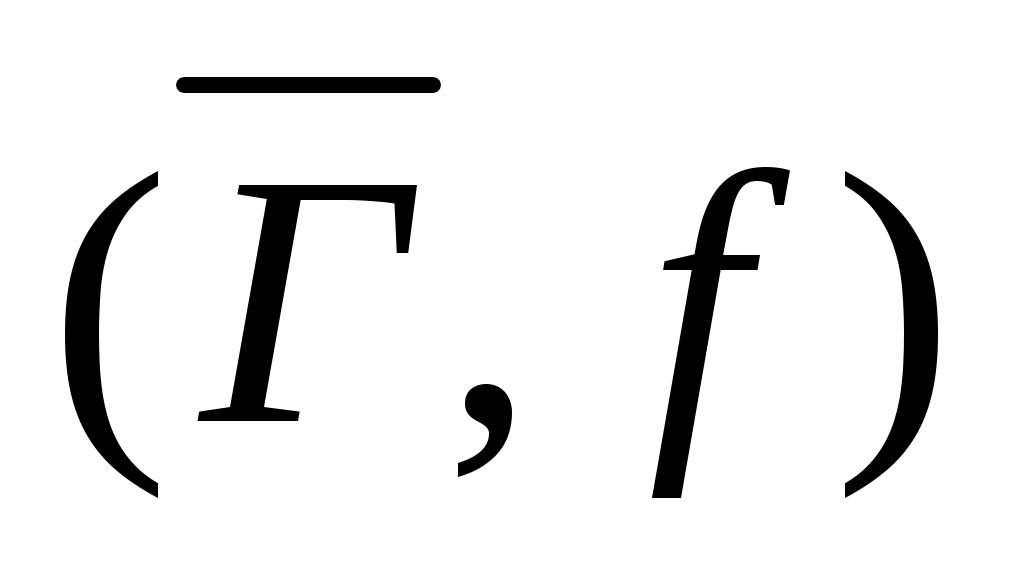 наз-ся сетью, а f-я f наз-ся f-цией пропускной способ-ти сети. Если f-я g: B→R удовлетворяет нерав-ву: gf, то g наз-ся потоком в сети. Пусть L: B→R – любая f-я и U, VА, символ h(U,V) будет обозначать сумму знач-й f-и h на ребрах (х,у)В, таких что хU, yV. Если U состоит из одной вершины a, то h(a,V) обозначает сумму весов ребер, начин-щихся в U и заканч-щихся в вершинах из V, аналогично h(U,a) – сумма знач-й f-и h на ребрах, начин.в U и заканч.в вершине а. Поток g: B→R в сети
наз-ся сетью, а f-я f наз-ся f-цией пропускной способ-ти сети. Если f-я g: B→R удовлетворяет нерав-ву: gf, то g наз-ся потоком в сети. Пусть L: B→R – любая f-я и U, VА, символ h(U,V) будет обозначать сумму знач-й f-и h на ребрах (х,у)В, таких что хU, yV. Если U состоит из одной вершины a, то h(a,V) обозначает сумму весов ребер, начин-щихся в U и заканч-щихся в вершинах из V, аналогично h(U,a) – сумма знач-й f-и h на ребрах, начин.в U и заканч.в вершине а. Поток g: B→R в сети 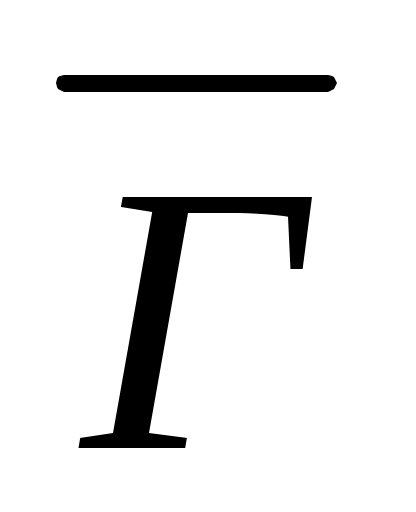 ,f наз-ся стационарным, если 2вершины U, VA и число WR такие, что выполн-ся след.усл-я: 1)g(U,A)-g(A,U)=W. 2)g(V,A)-g(A,V)=-W. 3)g(x,A)-g(A,x)=0 (д/любых х
,f наз-ся стационарным, если 2вершины U, VA и число WR такие, что выполн-ся след.усл-я: 1)g(U,A)-g(A,U)=W. 2)g(V,A)-g(A,V)=-W. 3)g(x,A)-g(A,x)=0 (д/любых х
А, но U и V. Известна след.классич.задача о max потоке: в дан.сети д/дан.источника и д/дан.стока найти стац.поток max-возможной величины. Можно док-ть, что дан.задача всегда имеет реш-е. Д/реш-я этой задачи сущ-ет много различ.алг-мов, одним из ктр явл-ся алг-м Форда-Фалкерсона. Постановка задачи: Д/опр-я max потока от некоторой вершины S графа (источника) к нектр вершине t графа (сток) использ-ся много различ.алг-мов. При этом кажд.дуге (орграф) (i,j) приписана нектр пропуск.способ-ть с(i,j), опр-щая max знач-е потока, ктр может протекать по дан.дуге. Алг-м Ф-Ф основан на «технике меток». Введем опр-я: разрезом наз-ся мн-во дуг, удаление ктр из сети приводит к разрыву всех путей, ведущих из S в t. Пропуск.способ-ть разреза – Сум.пропуск.способ-ть дуг его составляющих. Разрез с min пропуск.способ-тью наз-ся min разрезом. Т.Ф-Ф: величина кажд.потока из S в t не превосходит пропуск.способ-ти min разреза, разделяющего S и t, причем сущ-ет поток, достигающий этого знач-я. Если поток min, то по Т.Ф-Ф max поток не будет превышать 4ед-цы. Найти max поток, т.е. его распред-е по дугам, можно опр-ть методом перебора. Удачный выбор данных позволяет сделать программ.код компактным, но очевидно, что этот метод прим-м только д/небольших сетей. Техника меток Ф-Ф заключ-ся в послед-ном (итерацион.) построении max потока путем поиска на кажд.шаге увелич-щейся цепи, т.е. пути послед-ти д/потоков, по ктр можно увеличить. При этом узлы (вершины графа) спец.образом помеч-ся.
20. Определение паросочетаний в графе и их разновидностей. Двудольные графы и алгоритм выбора наибольшего паросочетания в двудольном графе.
Пусть Г = [А,В] – граф и S D – некот-е множ-во ребер в нем. Множество S назыв-ся паросочетанием, если любые два ребра из него не имеют общей вершины. Множ-во из одного ребра тоже будет назыв-ся паросочетанием, как и всякое пустое множ-во. Паросочетание называется максимальным, если к нему нельзя добавить ни одного ребра так, чтобы снова получ-сь паросочет-е. Паросочетание назыв-ся наибольшим, если оно состоит из наиб-го возможного колич-ва ребер. Очевидно, каждое наибольшее паросочетание явл. максимальным; обратное неверно.
Пример:
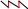
здесь красные ребра – максим-е, но не наибол-е паросочетание, а черные ребра – наибольшее паросочетание. Графы можно представлять матрицами. Матричные представления графов использ-ся при решении прикладных задач, особенно в тех случаях, когда при моделировании предметной области применяются алгебраические доказательства. Поиск наибольшего паросочетания в графе представляет собой классическую алгоритмическую задачу. Далее будет рассматриваться пример решения такой задачи для графов частного вида – графов двудольных. Граф Г = [А,В] называется двудольным, если его множество вершин А можно представить в виде объединения двух его непустых подмножеств А1, А2 без общих элементов так, что любое ребро из В будет иметь один конец в А1, а другой конец – в А2. таким образом, нет ни одного ребра, которое соединяло бы вершины из А1 или соединяло бы вершины из А2. Если считать, что А1 = {x1,…,xr}, А2 = {y1,…,yr}, то двудольный граф можно описать не только матрицей смежностей, но и матрицей двудольного графа: эта матрица – размером rs и если обозначать ее общий элемент через mij. Ясно, что такая матрица описывает граф однозначно, хотя является намного меньше по объему, чем матрица смежностей графа в этом случае. Когда множество А1 состоит из n вершин, а множество А2 состоит из mвершин и в двудольном графе проведены все возможные ребра, то говорят, что двудольный граф Г = [А,В] является полным двудольным графом и обозначают его символом Km,n. Далее описан алгоритм выбора наибольшего паросочетания в двудольном графе, опираясь на только что введенное понятие матрицы двудольного графа.
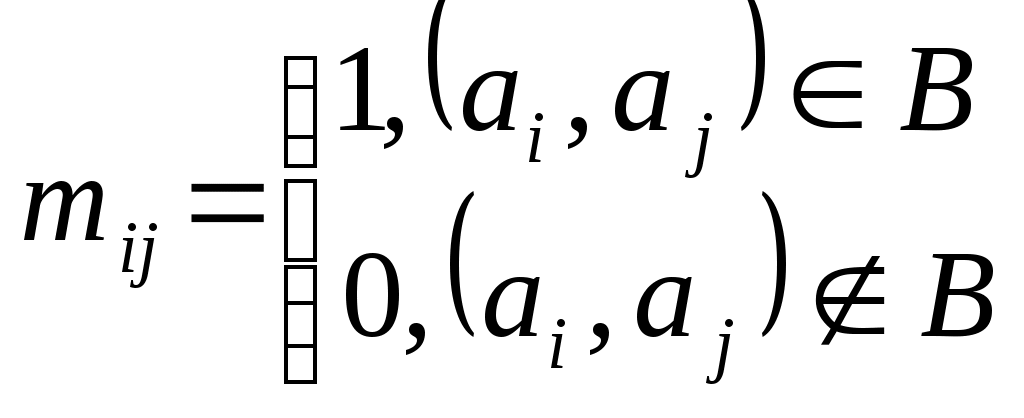
Эта матрица симметричная. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4).
| | 0 | 1 | 1 | 1 | 1 |
| | 1 | 0 | 1 | 0 | 0 |
| М = | 1 | 1 | 0 | 1 | 0 |
| | 1 | 0 | 1 | 0 | 0 |
| | 1 | 0 | 0 | 0 | 0 |
Другой вариант матричного представления — матрица инциденций является классическим способом в теории графов. Это не экономичный способ задания.
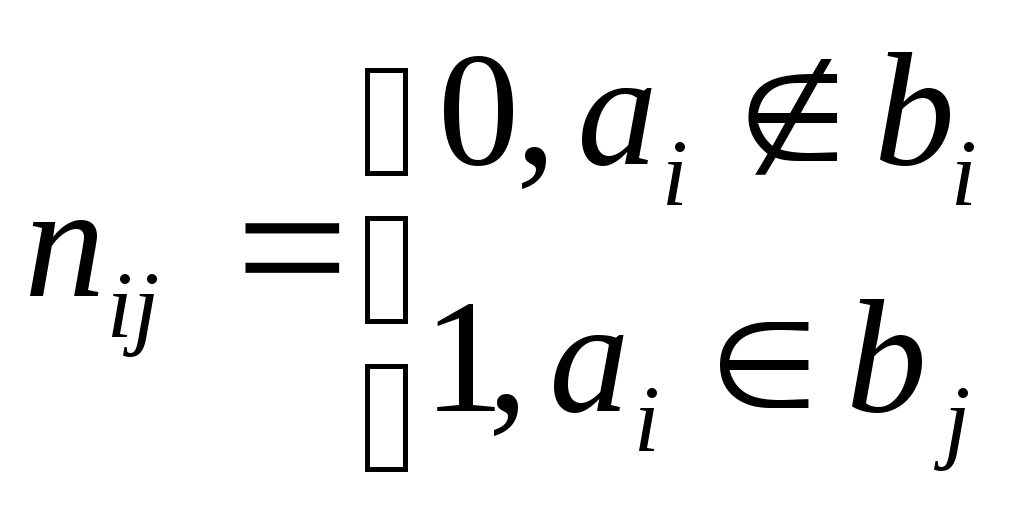
Данная матрица зависит от того как занумерованы ребра. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4). i=5; j=6.
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В данной матрицы в каждом столбце две 1, т.к. одному ребру всегда инцидентно только две вершины. Если в графе все вершины имеют степень 0, то матрица инцидентности не сущ-ет. В ЭВМ удобно представлять графы в виде матриц смежнотей: если направление ребра противоположено, то в матрицу составим (-1).
19. Путь в графе и связные комп-ты графа. Цепи, простые цепи, циклы, простые циклы. Операции удал-я вершины, уд-я ребра. Дерево и его особ-ти.
Графом называется пара множеств Г=[А,В], где А – любое непустое множество, а В – множество, которое является подмножеством множества V(A). Элементы из А называются вершинами графа, а элементы из В – его ребрами. Например, А={1,2,3,4,5}, В={(1,2),(2,3),(3,4),(1,5),(1,4),(3,1)}. Неупорядоченная пара вершин – ребро, а упорядоченная пара – дуга. Путем в графе Г называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным. Подграф содержит подмножество вершин графа и все соединяющие их рёбра. Компонента связности – максимально связанный подграф. Путь без повтор-ся ребер наз-ся цепью, а цепь без повтор-ся вершин называется простой. Цепь, в кот-й совпадают концевые вершины наз-ся циклом, а цикл, в кто-м нет повто-х вершин, кроме концевых, наз-ся простым. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги – ориентированным или орграфом. Граф называется петлей, если его начало и конец совпадают. Удаление ребра. Г=[А,В] и a А, b В. Удалить ребро b это значит построить новый граф Г`=[А` ,В`],
в кот-м А`=А, В`=В\b





Удаление вершин. Г=[А,В] и a А, чтобы удалить вершину а из Г=[А,В] нужно, построить граф новый Г`=[А` ,В`], в кот-м А`=А\{a}, В` получится из В удал-е все ребра. (а будет на пересечении)
Д
 ерево
ерево
– это граф без циклов. Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины. (первый явл., а второй не явл.). Если Г=[А,В] явл. Деревом и число его вершин = р, то о числе ребер можно сказать совершенно опред-но: в дереве имеется еще одна особенность любые две вершины в дереве связаны и при этом единственной простой цепью.
29. Сети и потоки в сетях. Задача о максимальном потоке и алгоритм Форда–Фалкерсона.
Пусть
А, но U и V. Известна след.классич.задача о max потоке: в дан.сети д/дан.источника и д/дан.стока найти стац.поток max-возможной величины. Можно док-ть, что дан.задача всегда имеет реш-е. Д/реш-я этой задачи сущ-ет много различ.алг-мов, одним из ктр явл-ся алг-м Форда-Фалкерсона. Постановка задачи: Д/опр-я max потока от некоторой вершины S графа (источника) к нектр вершине t графа (сток) использ-ся много различ.алг-мов. При этом кажд.дуге (орграф) (i,j) приписана нектр пропуск.способ-ть с(i,j), опр-щая max знач-е потока, ктр может протекать по дан.дуге. Алг-м Ф-Ф основан на «технике меток». Введем опр-я: разрезом наз-ся мн-во дуг, удаление ктр из сети приводит к разрыву всех путей, ведущих из S в t. Пропуск.способ-ть разреза – Сум.пропуск.способ-ть дуг его составляющих. Разрез с min пропуск.способ-тью наз-ся min разрезом. Т.Ф-Ф: величина кажд.потока из S в t не превосходит пропуск.способ-ти min разреза, разделяющего S и t, причем сущ-ет поток, достигающий этого знач-я. Если поток min, то по Т.Ф-Ф max поток не будет превышать 4ед-цы. Найти max поток, т.е. его распред-е по дугам, можно опр-ть методом перебора. Удачный выбор данных позволяет сделать программ.код компактным, но очевидно, что этот метод прим-м только д/небольших сетей. Техника меток Ф-Ф заключ-ся в послед-ном (итерацион.) построении max потока путем поиска на кажд.шаге увелич-щейся цепи, т.е. пути послед-ти д/потоков, по ктр можно увеличить. При этом узлы (вершины графа) спец.образом помеч-ся.
20. Определение паросочетаний в графе и их разновидностей. Двудольные графы и алгоритм выбора наибольшего паросочетания в двудольном графе.
Пусть Г = [А,В] – граф и S D – некот-е множ-во ребер в нем. Множество S назыв-ся паросочетанием, если любые два ребра из него не имеют общей вершины. Множ-во из одного ребра тоже будет назыв-ся паросочетанием, как и всякое пустое множ-во. Паросочетание называется максимальным, если к нему нельзя добавить ни одного ребра так, чтобы снова получ-сь паросочет-е. Паросочетание назыв-ся наибольшим, если оно состоит из наиб-го возможного колич-ва ребер. Очевидно, каждое наибольшее паросочетание явл. максимальным; обратное неверно.
Пример:
здесь красные ребра – максим-е, но не наибол-е паросочетание, а черные ребра – наибольшее паросочетание. Графы можно представлять матрицами. Матричные представления графов использ-ся при решении прикладных задач, особенно в тех случаях, когда при моделировании предметной области применяются алгебраические доказательства. Поиск наибольшего паросочетания в графе представляет собой классическую алгоритмическую задачу. Далее будет рассматриваться пример решения такой задачи для графов частного вида – графов двудольных. Граф Г = [А,В] называется двудольным, если его множество вершин А можно представить в виде объединения двух его непустых подмножеств А1, А2 без общих элементов так, что любое ребро из В будет иметь один конец в А1, а другой конец – в А2. таким образом, нет ни одного ребра, которое соединяло бы вершины из А1 или соединяло бы вершины из А2. Если считать, что А1 = {x1,…,xr}, А2 = {y1,…,yr}, то двудольный граф можно описать не только матрицей смежностей, но и матрицей двудольного графа: эта матрица – размером rs и если обозначать ее общий элемент через mij. Ясно, что такая матрица описывает граф однозначно, хотя является намного меньше по объему, чем матрица смежностей графа в этом случае. Когда множество А1 состоит из n вершин, а множество А2 состоит из mвершин и в двудольном графе проведены все возможные ребра, то говорят, что двудольный граф Г = [А,В] является полным двудольным графом и обозначают его символом Km,n. Далее описан алгоритм выбора наибольшего паросочетания в двудольном графе, опираясь на только что введенное понятие матрицы двудольного графа.


