ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
имеют разные знаки; б)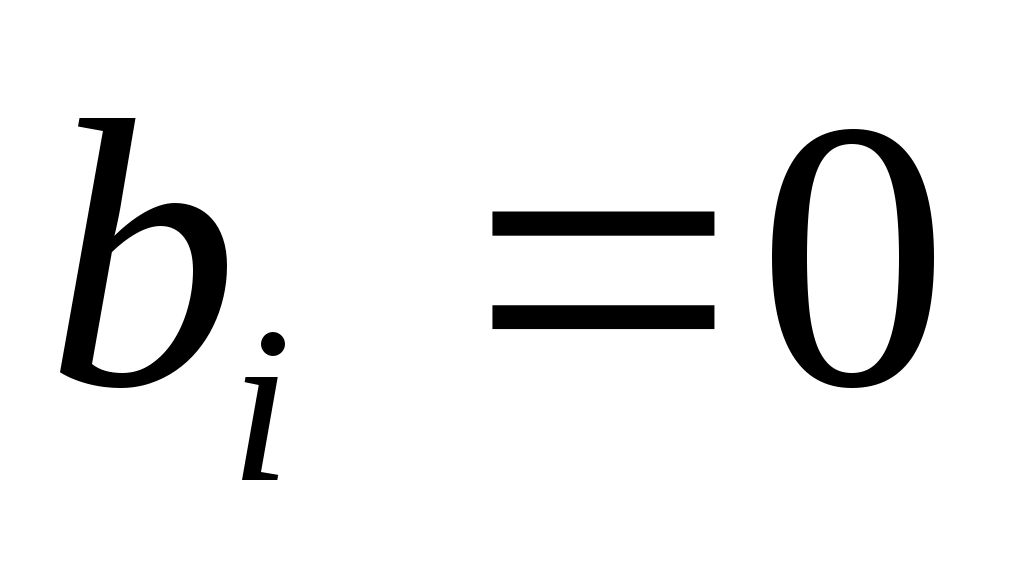 и
и 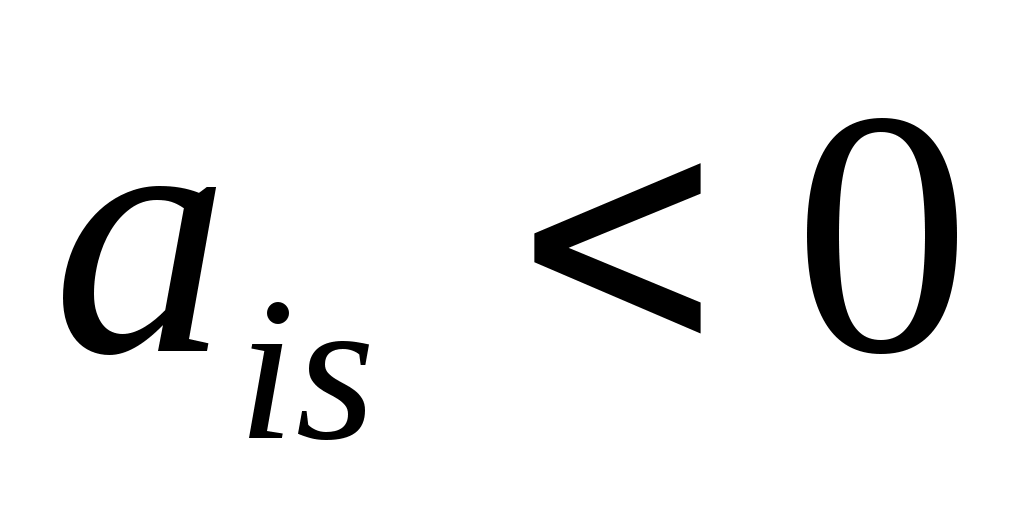 ; в)
; в)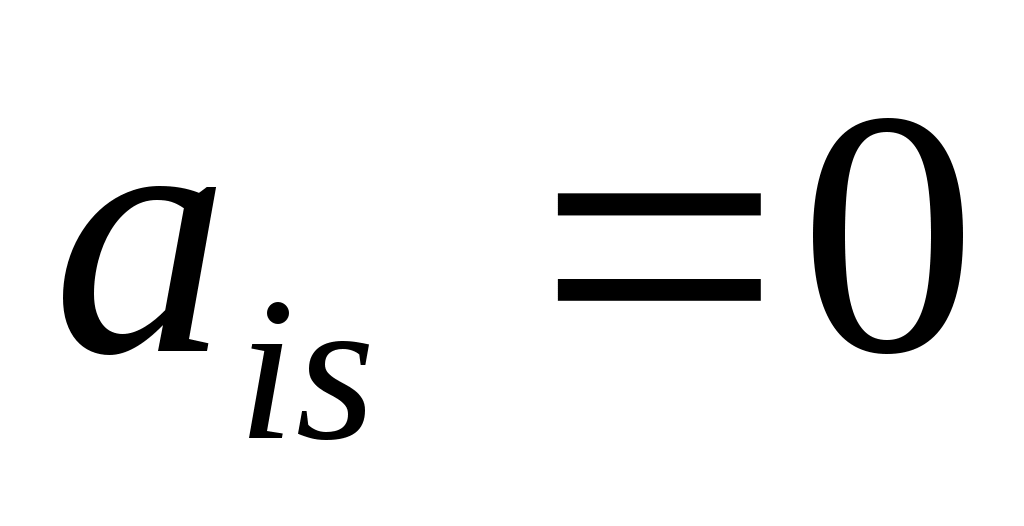 ; г)0, если
; г)0, если 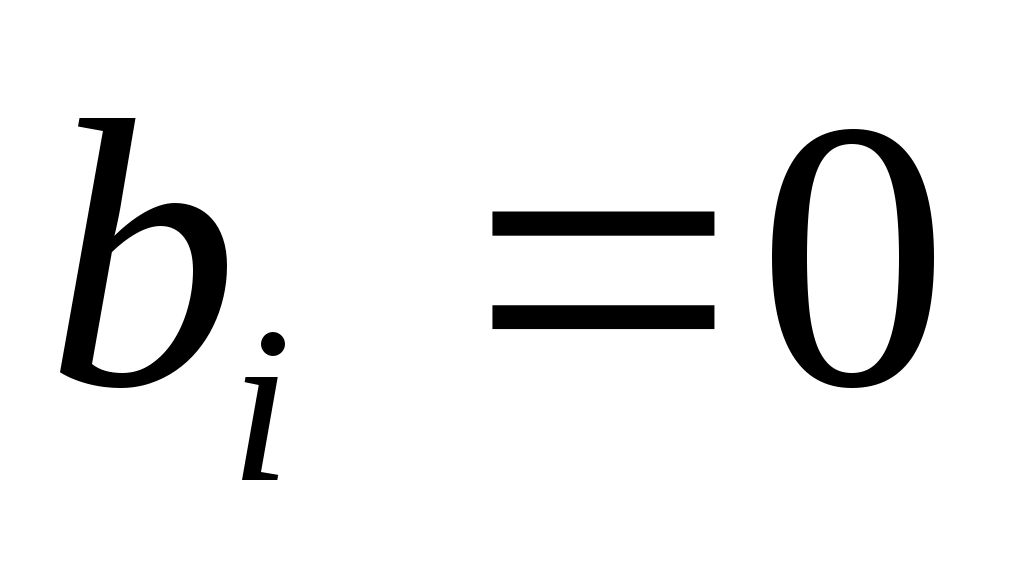 и
и  ; д)
; д)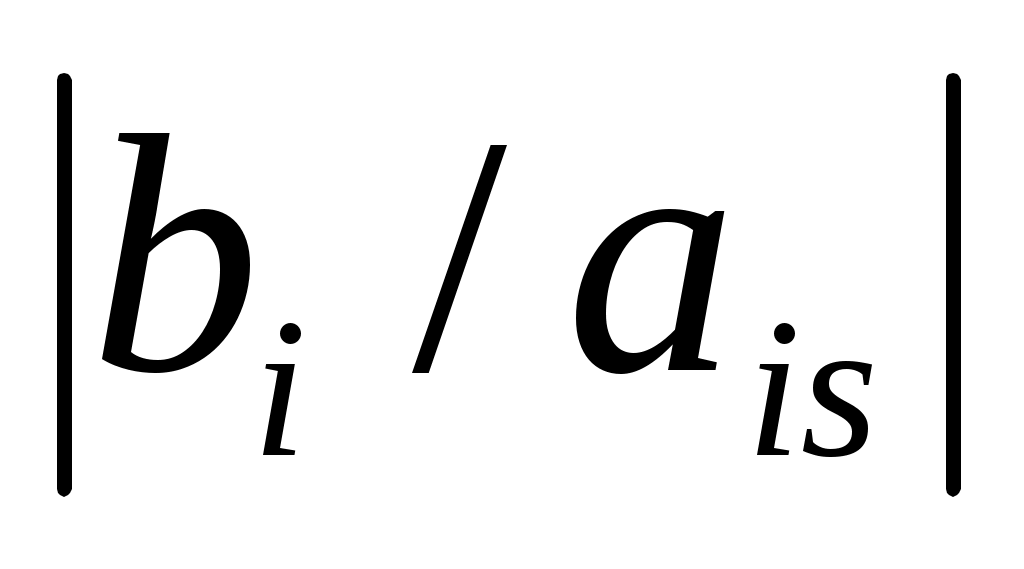 , если
, если 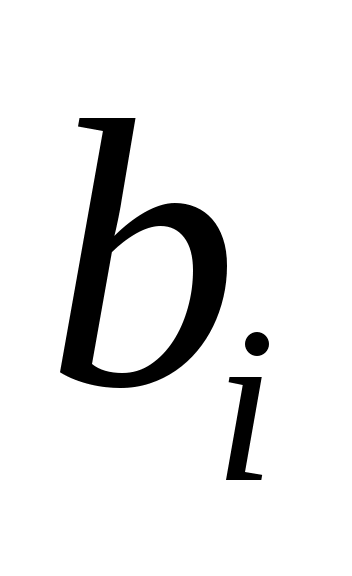 и
и  имеют одинак.знаки. Опр-ем min
имеют одинак.знаки. Опр-ем min 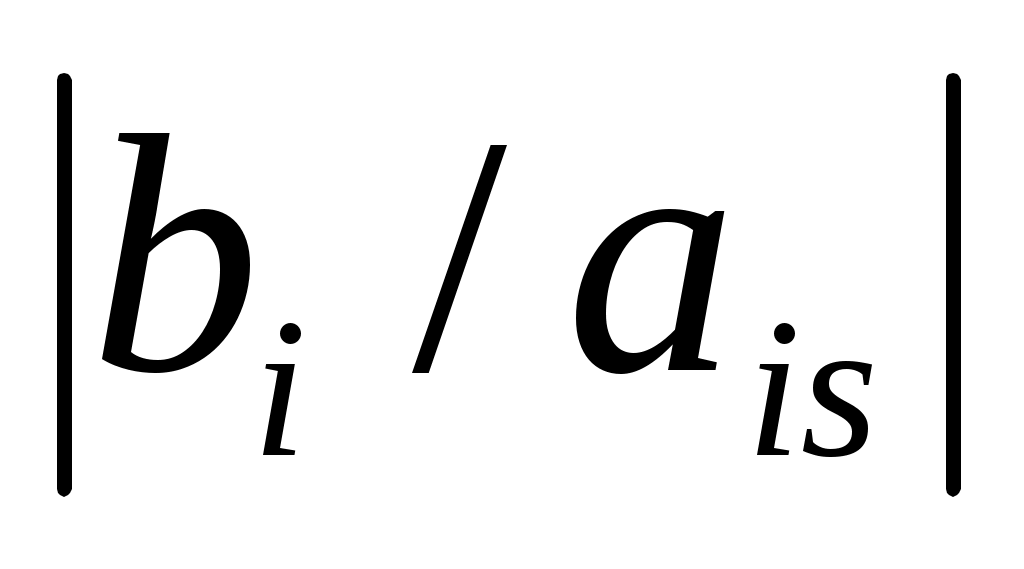 . Если конечного min нет, то задача не имеет конечного оптимума, т.е.
. Если конечного min нет, то задача не имеет конечного оптимума, т.е. 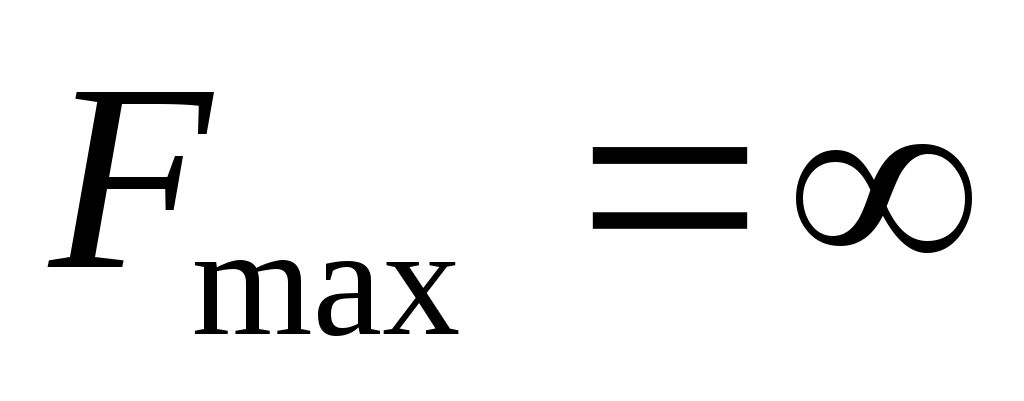 . Если min конечен, то выбираем строку q, на ктр он достиг-ся (если их неск-ко, то выбираем любую) и назовем ее разрешающей строкой. На пересечении разреш.столбца и разреш.строки нах-ся разрешающий элемент
. Если min конечен, то выбираем строку q, на ктр он достиг-ся (если их неск-ко, то выбираем любую) и назовем ее разрешающей строкой. На пересечении разреш.столбца и разреш.строки нах-ся разрешающий элемент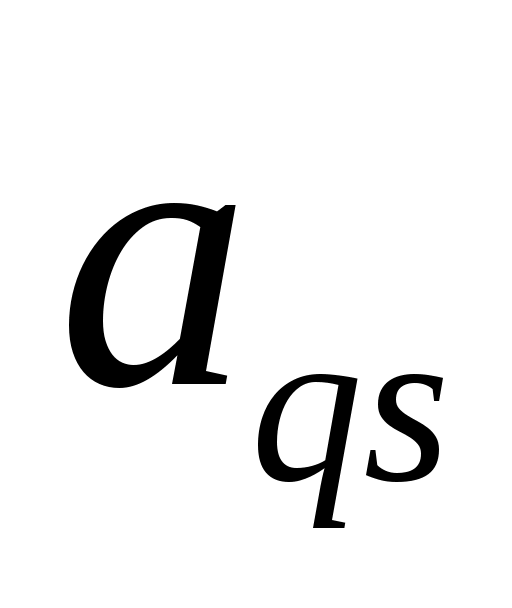 . г)Переходим к
. г)Переходим к
след.таблице по след.правилам: а)в лев.столбце записываем новый базис: вместо осн.пер-ных хq записываем хs; б)в столбцах, соотв-щих осн.пер-ным, проставляем: 1 – против «своей» осн.пер-ной, 0 – против «чужой» осн.пер-ной, 0 – в послед.строке д/всех осн.пер-ных; в)нов.строку с № q получаем из старой строки делением на разреш.столбец
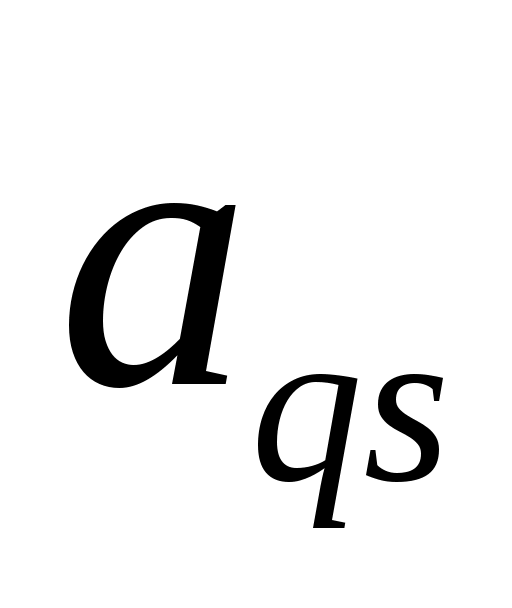 ;
;
г)все остальные пер-ные пересчитываем по правилу прямоугольника. Далее переходим к пункту 2.
пересчитываем по правилу прямоугольника. Далее переходим к пункту 2.
2.MIN. Сначала также преобраз-ся сис-ма нерав-в в сис-му ур-ий, выражаем осн.пер-ные через неосн. Критерий оптим-ти при отыскании min лин.f-и: если в выраж-и лин.f-и через неосн.пер-ные отсутствуют отриц.коэф-ты при неосн.пер-ных, то реш-е оптимально. Смотрим, есть ли в итог.столбце (свобод.членов) отриц.знаки. Если да, то это явл-ся свидетельством того, что дан.план нельзя считать допустимым. Ликвидация отриц.чисел в итог.столбце начин-ся с наибольшего по абсолют.величине (это будет ключевая строка)
. Найдем ключ.столбец. Д/этого нужно эл-ты цел.строки разделить на эл-ты ключ.строки (оц.отнош-я) д/столбцов. Из получен.отнош-й выбираем наименьшее. На пересеч-и ключ.строки и столбца нах-ся ключ.эл-т. Далее все происходит также.
10. Транспортная задача.
# Имеется m пунктов отправления (пунктов произв-ва) Аi …, Аm, в ктр сосредоточены запасы однород.продуктов в кол-ве a1, ..., аm ед-ц. Имеется n пунктов назнач-я (пунктов потребления) В1, ..., Вn, потреб-ть ктр в указанных продуктах составляет b1, ..., bn ед-ц. Известны также транспорт.расходы Сij, связанные с перевозкой ед-цы продукта из пункта Ai в пункт Вj, (i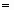 1, …, m; j
1, …, m; j 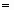 1, ..., n). Постановка задачи: Найти V перевозок д/кажд.пары «поставщ.-потреб.» так, чтобы: 1)мощ-ти всех пост-ков были реализованы; 2)спросы всех потреб-лей были удовлетворены; 3)затраты на перевозку были min. Особен-ти эк.-мат.модели ТЗ: 1)сис-мы огранич-й – есть сис-мы ур-ий; 2)коэф-ты при неизвестных в сис-мах огранич-й = 1 или 0; 3)кажд.переменная входит в сис-му огранич-й 2раза – 1раз в I сис-му и 1раз во II. Всякое неотриц.реш-е сис-мы лин.ур-й, опр-мое матрицей X=(xij) (i=1, …, m; j=1, ..., n), наз-ся планом ТЗ. План X=(xij)(i=1, …, m; j=1, ..., n), при ктр f-я принимает свое min значение, наз-ся оптимал.планом ТЗ. Если мощ-ть всех пост-ков=сум.мощ-ти потреб-лей, то такие задачи наз-ся закрытыми, в против.случае – открытого типа. Т: число r осн.(базисных) переменных закрытой ТЗ = m+n-1 (m-число пост-ков, n-потреб-лей). Кажд.разбиению переменных xij задачи на осн.(базисные) и неосн.(свобод.) соотв-ет базис.реш-е и, как следствие, заполнение таблицы поставок, ктр также наз-ся базисным. Др.словами, распред-е поставок наз-ся базисным, если переменные, соотв-щие заполненным клеткам, можно принять за осн.переменные. Клетки, отвечающие базис.переменным, наз-ся базисными, а клетки, соотв-щие свобод.перемен., свободными или пустыми.
1, ..., n). Постановка задачи: Найти V перевозок д/кажд.пары «поставщ.-потреб.» так, чтобы: 1)мощ-ти всех пост-ков были реализованы; 2)спросы всех потреб-лей были удовлетворены; 3)затраты на перевозку были min. Особен-ти эк.-мат.модели ТЗ: 1)сис-мы огранич-й – есть сис-мы ур-ий; 2)коэф-ты при неизвестных в сис-мах огранич-й = 1 или 0; 3)кажд.переменная входит в сис-му огранич-й 2раза – 1раз в I сис-му и 1раз во II. Всякое неотриц.реш-е сис-мы лин.ур-й, опр-мое матрицей X=(xij) (i=1, …, m; j=1, ..., n), наз-ся планом ТЗ. План X=(xij)(i=1, …, m; j=1, ..., n), при ктр f-я принимает свое min значение, наз-ся оптимал.планом ТЗ. Если мощ-ть всех пост-ков=сум.мощ-ти потреб-лей, то такие задачи наз-ся закрытыми, в против.случае – открытого типа. Т: число r осн.(базисных) переменных закрытой ТЗ = m+n-1 (m-число пост-ков, n-потреб-лей). Кажд.разбиению переменных xij задачи на осн.(базисные) и неосн.(свобод.) соотв-ет базис.реш-е и, как следствие, заполнение таблицы поставок, ктр также наз-ся базисным. Др.словами, распред-е поставок наз-ся базисным, если переменные, соотв-щие заполненным клеткам, можно принять за осн.переменные. Клетки, отвечающие базис.переменным, наз-ся базисными, а клетки, соотв-щие свобод.перемен., свободными или пустыми.
11. Методы нахож-я начал-го реш-я трансп-й з-чи.
Д/начала нахождения оптимал.решения требуется найти исх.базисное распред-е поставок – опорный план. Рассмотрим метод «сев.-запад.угла» д/нахожд-я опор.плана. Переносим все коэф-ты из ур-й в таблицу – опорное реш-е выполнено. При этом цел.f-я принимает знач-е суммы произведений верх.угла клетки на нижний угол. Надо, чтобы число заполненных клеток было = m (мощ-ть пост-ков) + n (спрос потреб-лей) - 1. Недостаток этого метода в том, что он построен без учета знач-й коэф-тов затрат задачи. С др.стороны дан.метод допускает модификацию, лишенную этого недостатка, т.е. на кажд.шаге max-возможную поставку следует давать не в сев.-запад.клетку оставшейся таблицы, а в клетку с наим.коэф-том затрат. При этом распред-е
поставок оказыв-ся ближе к оптимуму, чем распред-е, полученное методом сев.-запад.угла. Метод минимального элемента. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
12. Метод потенц-в в решении трансп-й задачи.
Необх-мо сделать оценку свобод.клеток. Сущ-ть метода потенциалов состоит в том, что д/кажд.строки и кажд.столбца таблицы опр-ют спец.числа, называемые потенциалами. С помощью них можно установить, нужно ли заполнять свобод.клетку таблицы или ее можно оставить незаполненной. Потенциалы строк и столбцов опр-ся по заполнен.клеткам, нах-щимся на их пересечении. Эл-т заполнен.клетки должен равняться сумме потенциалов строки и столбца, на пересеч-и ктр нах-ся эта заполнен.клетка. Д/начала вычислений I потенциал д/строки или столбца приним-ся условно = 0, а все остальные потенциалы опр-ся с помощью эл-тов заполнен.клеток. Обознач-я: Vj – потенциалы столбцов, Ui – строк, Сij – эл-ты заполнения клеток. Сij = Ui + Vj . После того, как потенциалы столбцов и строк опр-ны, выясняется, явл-ся ли план оптимальным или нет. С этой целью д/кажд.свобод.клетки вычисл-ся сумма потенциалов строк и столбцов, на пересеч-и ктр нах-ся эта клетка. Сравнение суммы потенциалов с величиной эл-та в свобод.клетках позволяет опр-ть, нужно ли заполнять эту клетку или ее нужно оставить свобод. При решении задачи на min (max) не заполн-ся те свобод.клетки, в ктр сумма потенциалов < (>) величины эл-та. Если хар-ка, знач-е ктр = Сij – (Ui + Vj ) положит. (отриц.), то свобод.клетка не заполн-ся при решении задач на min (на max). Свобод.клетки, имеющие нулевое знач-е хар-ки, показывают на то, что их
заполнение приведет к перераспред-ю поставок, но объем работ останется неизменным. После этого числа заносим в таблицу и опр-ем связь с неск-кими незаполнен.клетками. Эта связь выявл-ся путем построения замкнутых многоуг-ков, вершинами ктр явл-ся клетки таблицы. Углы в этих многоуг-ках должны быть прямыми. Одна вершина нах-ся в свобод.клетке, а все остальные – в заполнен. Многоуг-к имеет четное кол-во вершин. В этом цикле пересчета + помечены те клетки, поставка в ктр увелич., и «-» – уменьш-ся. Замечание: иногда д/произвол.означенного цикла вводится понятие оценка цикла – алгебраич.сумма коэф-тов, стоящих в вершинах цикла, взятых с соотв-щими знаками. Д/кажд.свобод.клетки базис.распред-я поставок сущ-ет и при том единствен.цикл пересчета. Причем, операция означивания цикла явл-ся корректной. Т.(о потенциалах): оценка свобод.клетки не измен-ся, если к коэф-там затрат некоторой строки (столбца) таблицы поставок прибавить некоторое число. Изменение коэф-тов затрат можно начинать с любого столбца (строки). Потенциал столбца (строки), избранного д/начала, может быть произвольным. Остальные соотв-но необх-мо пересчитывать.
13. Общий вид задач нелинейного программир-я. Графический метод решения задач нелинейного программир-я.
Во многих эк.моделях исследов-я операций завис-ти между постоянными и перемен.факторами лишь в I приближ-и можно считать лин., более детальное рассмотр-е позволяет обнаружить их нелин-ть. Как пр-ло, такие показ-ли, как прибыль, с/стоим-ть, капитал.затраты на произв-во и др., в действит-ти зависят от объема произв-ва, расхода ресурсов и т.п. нелинейно. К класс.методам оптимизации относ-ся классы Нелин.задач и др. Задачу оптимизации можно сформулировать так: найти переменные х1…хn, удовлетворяющие сис-ме ур-й
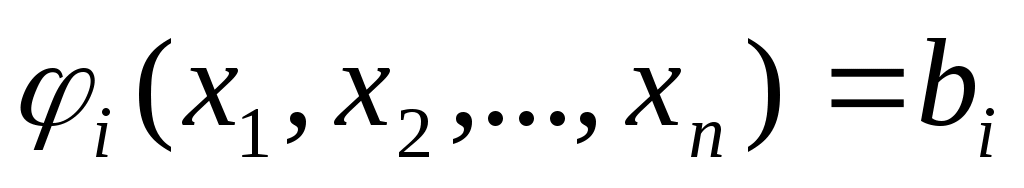 , где i=1,…, m, и обращающие в max (min) целевую f-ю
, где i=1,…, m, и обращающие в max (min) целевую f-ю
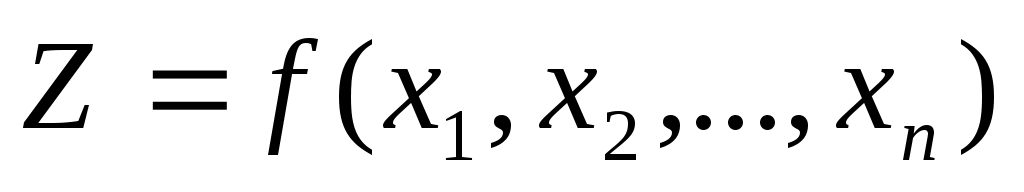 . При этом переменные х1…хn не явл-ся дискретными. F-и
. При этом переменные х1…хn не явл-ся дискретными. F-и
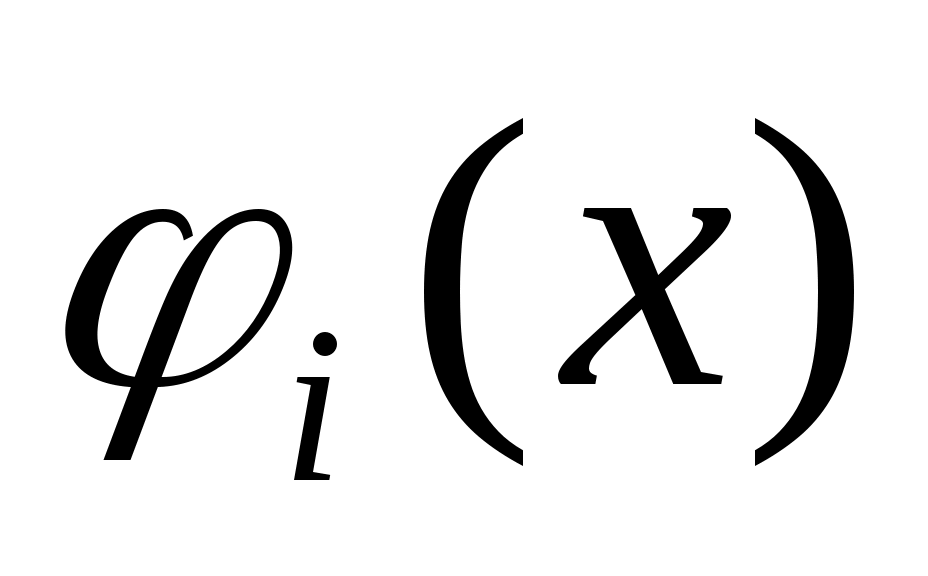 и f(х) явл-ся непрерывными и имеют, по
и f(х) явл-ся непрерывными и имеют, по
кр.мере, частные производные II порядка. #задача Нелин.прогр.: дан.предпр-е д/произв-ва какого-то продукта расходует 2ср-ва в кол-ве х
1 и х2. Это факторы произв-ва (машины и труд), 2различных вида сырья… Факторы машины и труд взаимозаменяемы или в с/хоз-ве взаимоз.факторами считаются посевные площади и кол-во удобрений. Vпроизв-ва, выраженный в натурал.или стоим.ед-цах, явл-ся f-ей затрат произв-ва
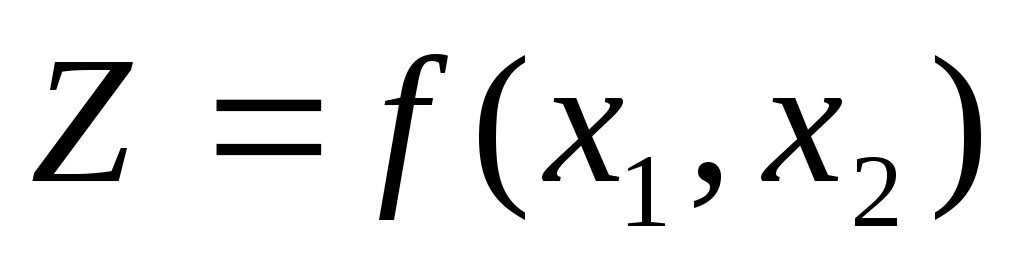 . Эта завис-ть наз-ся произв-венной f-ей. Издержки зависят от расхода обоих факторов (х1 и х2) и от цен этих факторов (с1 и с2). Совокупные издержки выраж-ся формулой
. Эта завис-ть наз-ся произв-венной f-ей. Издержки зависят от расхода обоих факторов (х1 и х2) и от цен этих факторов (с1 и с2). Совокупные издержки выраж-ся формулой
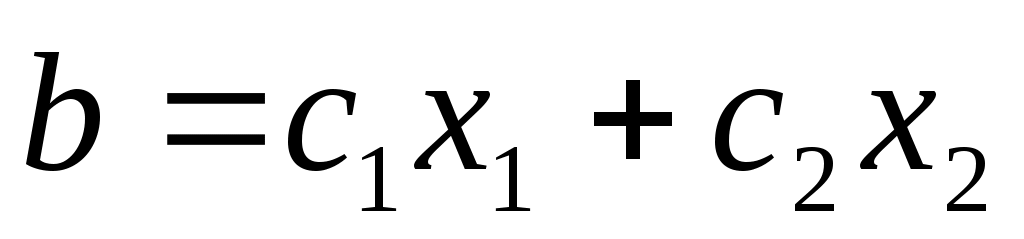 . Требуется при дан.издержках опр-ть такое кол-во факторов произв-ва, ктр max-ет V продукции Z. Мат.модель этой задачи имеет вид: опр-ть такие переменные х1 и х2, удовлетвор-щие усл-ям:
. Требуется при дан.издержках опр-ть такое кол-во факторов произв-ва, ктр max-ет V продукции Z. Мат.модель этой задачи имеет вид: опр-ть такие переменные х1 и х2, удовлетвор-щие усл-ям:
1)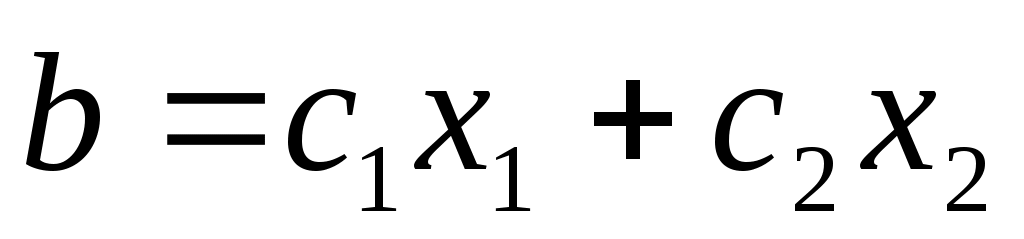 ; 2)
; 2)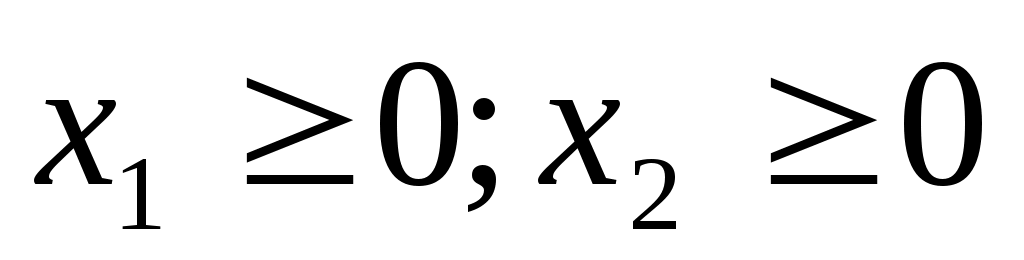 ;
;
3)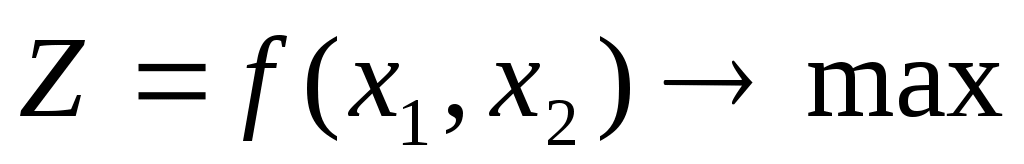 . Положим, что
. Положим, что
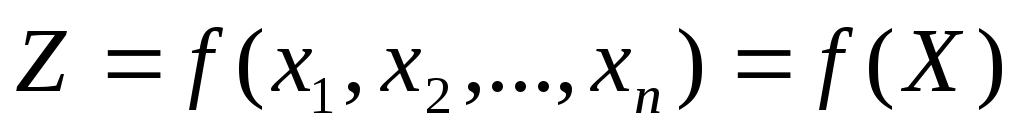 дважды диф-ма в т.
дважды диф-ма в т.
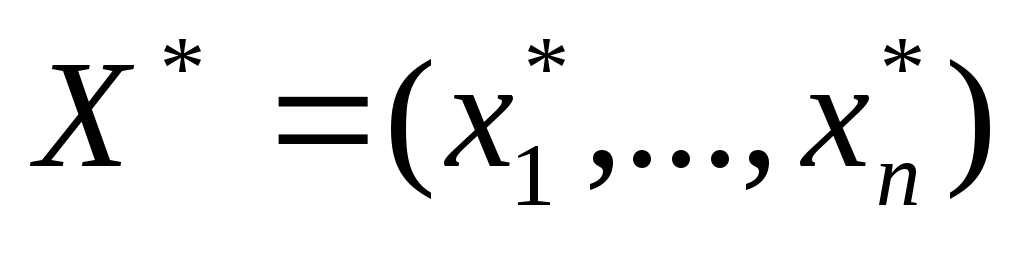 ,
,
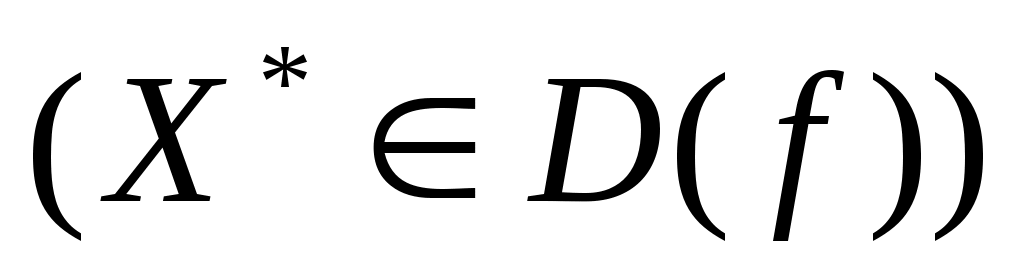 и в некоторой ее окрест-ти. Точка X*, в ктр все частные производные f-и
и в некоторой ее окрест-ти. Точка X*, в ктр все частные производные f-и
 = 0, наз-ся стационарной точкой. Локал.экстр. Необх.усл-е экстремума. Если в точке х0 f-я имеет экстремум, то
= 0, наз-ся стационарной точкой. Локал.экстр. Необх.усл-е экстремума. Если в точке х0 f-я имеет экстремум, то
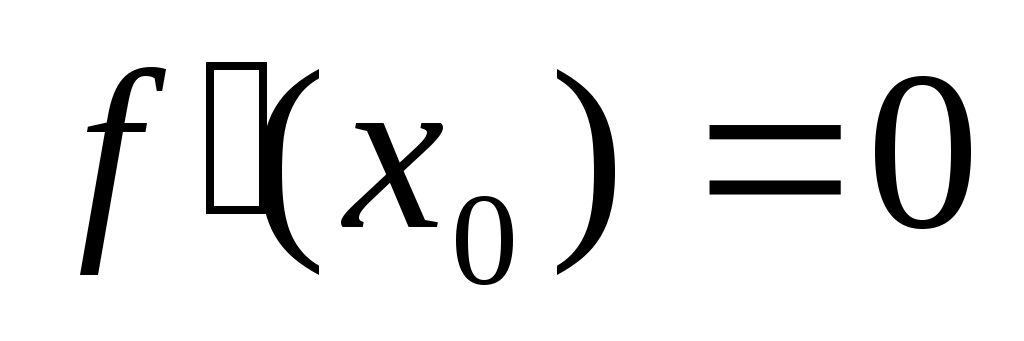 . Дост.усл-я экстремума: 1)если х0 – точка max (min), то при переходе через нее
. Дост.усл-я экстремума: 1)если х0 – точка max (min), то при переходе через нее 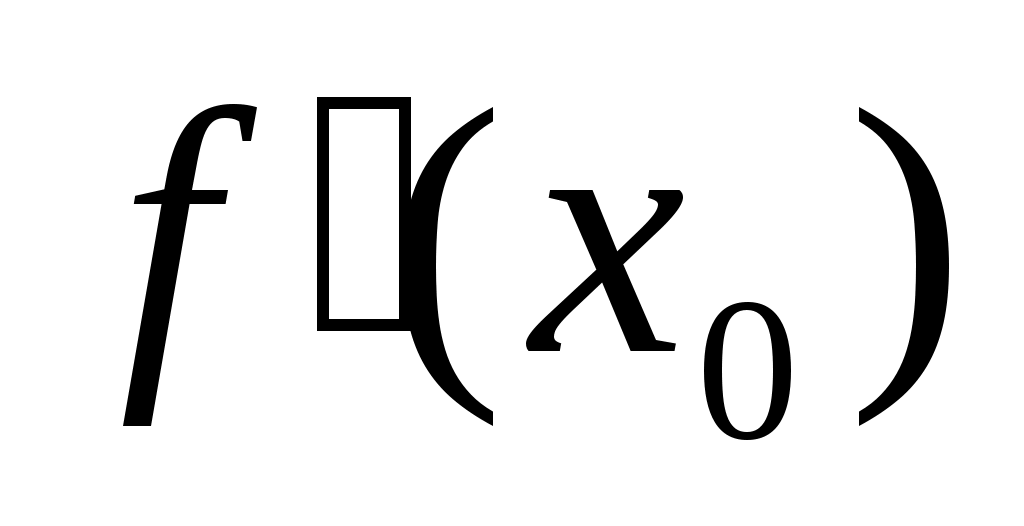 меняет знак с + на – (с – на +). 2)если х0 – точка max (min), то
меняет знак с + на – (с – на +). 2)если х0 – точка max (min), то  (
(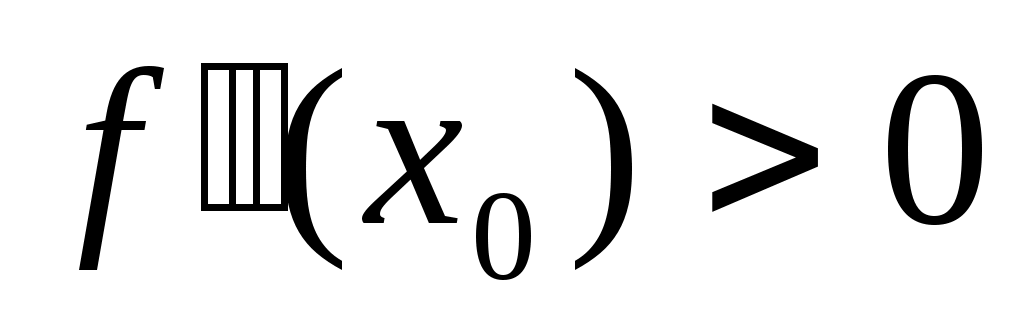 ). 3)если
). 3)если 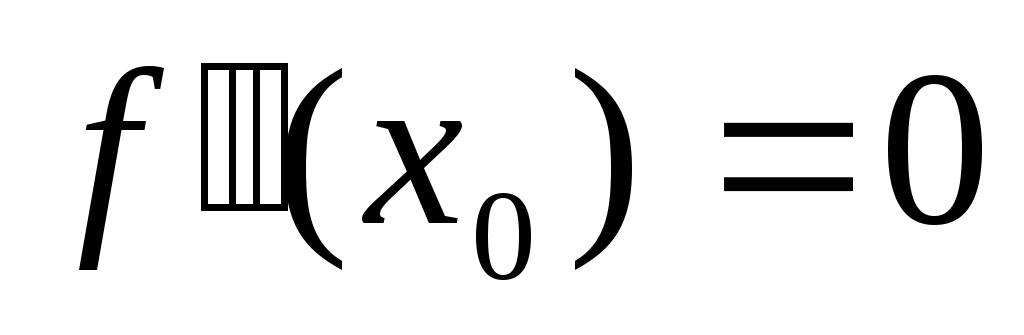 , то вопрос о сущ-и экстремума остается открытым. Дост.усл-е сущ-я экстремума: 1)если В2-АС<0, то сущ-ет экстремум, причем, если А<0, то х0 – точка max, если А>0, то х
, то вопрос о сущ-и экстремума остается открытым. Дост.усл-е сущ-я экстремума: 1)если В2-АС<0, то сущ-ет экстремум, причем, если А<0, то х0 – точка max, если А>0, то х
след.таблице по след.правилам: а)в лев.столбце записываем новый базис: вместо осн.пер-ных хq записываем хs; б)в столбцах, соотв-щих осн.пер-ным, проставляем: 1 – против «своей» осн.пер-ной, 0 – против «чужой» осн.пер-ной, 0 – в послед.строке д/всех осн.пер-ных; в)нов.строку с № q получаем из старой строки делением на разреш.столбец
г)все остальные пер-ные
2.MIN. Сначала также преобраз-ся сис-ма нерав-в в сис-му ур-ий, выражаем осн.пер-ные через неосн. Критерий оптим-ти при отыскании min лин.f-и: если в выраж-и лин.f-и через неосн.пер-ные отсутствуют отриц.коэф-ты при неосн.пер-ных, то реш-е оптимально. Смотрим, есть ли в итог.столбце (свобод.членов) отриц.знаки. Если да, то это явл-ся свидетельством того, что дан.план нельзя считать допустимым. Ликвидация отриц.чисел в итог.столбце начин-ся с наибольшего по абсолют.величине (это будет ключевая строка)
. Найдем ключ.столбец. Д/этого нужно эл-ты цел.строки разделить на эл-ты ключ.строки (оц.отнош-я) д/столбцов. Из получен.отнош-й выбираем наименьшее. На пересеч-и ключ.строки и столбца нах-ся ключ.эл-т. Далее все происходит также.
10. Транспортная задача.
# Имеется m пунктов отправления (пунктов произв-ва) Аi …, Аm, в ктр сосредоточены запасы однород.продуктов в кол-ве a1, ..., аm ед-ц. Имеется n пунктов назнач-я (пунктов потребления) В1, ..., Вn, потреб-ть ктр в указанных продуктах составляет b1, ..., bn ед-ц. Известны также транспорт.расходы Сij, связанные с перевозкой ед-цы продукта из пункта Ai в пункт Вj, (i
11. Методы нахож-я начал-го реш-я трансп-й з-чи.
Д/начала нахождения оптимал.решения требуется найти исх.базисное распред-е поставок – опорный план. Рассмотрим метод «сев.-запад.угла» д/нахожд-я опор.плана. Переносим все коэф-ты из ур-й в таблицу – опорное реш-е выполнено. При этом цел.f-я принимает знач-е суммы произведений верх.угла клетки на нижний угол. Надо, чтобы число заполненных клеток было = m (мощ-ть пост-ков) + n (спрос потреб-лей) - 1. Недостаток этого метода в том, что он построен без учета знач-й коэф-тов затрат задачи. С др.стороны дан.метод допускает модификацию, лишенную этого недостатка, т.е. на кажд.шаге max-возможную поставку следует давать не в сев.-запад.клетку оставшейся таблицы, а в клетку с наим.коэф-том затрат. При этом распред-е
поставок оказыв-ся ближе к оптимуму, чем распред-е, полученное методом сев.-запад.угла. Метод минимального элемента. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
12. Метод потенц-в в решении трансп-й задачи.
Необх-мо сделать оценку свобод.клеток. Сущ-ть метода потенциалов состоит в том, что д/кажд.строки и кажд.столбца таблицы опр-ют спец.числа, называемые потенциалами. С помощью них можно установить, нужно ли заполнять свобод.клетку таблицы или ее можно оставить незаполненной. Потенциалы строк и столбцов опр-ся по заполнен.клеткам, нах-щимся на их пересечении. Эл-т заполнен.клетки должен равняться сумме потенциалов строки и столбца, на пересеч-и ктр нах-ся эта заполнен.клетка. Д/начала вычислений I потенциал д/строки или столбца приним-ся условно = 0, а все остальные потенциалы опр-ся с помощью эл-тов заполнен.клеток. Обознач-я: Vj – потенциалы столбцов, Ui – строк, Сij – эл-ты заполнения клеток. Сij = Ui + Vj . После того, как потенциалы столбцов и строк опр-ны, выясняется, явл-ся ли план оптимальным или нет. С этой целью д/кажд.свобод.клетки вычисл-ся сумма потенциалов строк и столбцов, на пересеч-и ктр нах-ся эта клетка. Сравнение суммы потенциалов с величиной эл-та в свобод.клетках позволяет опр-ть, нужно ли заполнять эту клетку или ее нужно оставить свобод. При решении задачи на min (max) не заполн-ся те свобод.клетки, в ктр сумма потенциалов < (>) величины эл-та. Если хар-ка, знач-е ктр = Сij – (Ui + Vj ) положит. (отриц.), то свобод.клетка не заполн-ся при решении задач на min (на max). Свобод.клетки, имеющие нулевое знач-е хар-ки, показывают на то, что их
заполнение приведет к перераспред-ю поставок, но объем работ останется неизменным. После этого числа заносим в таблицу и опр-ем связь с неск-кими незаполнен.клетками. Эта связь выявл-ся путем построения замкнутых многоуг-ков, вершинами ктр явл-ся клетки таблицы. Углы в этих многоуг-ках должны быть прямыми. Одна вершина нах-ся в свобод.клетке, а все остальные – в заполнен. Многоуг-к имеет четное кол-во вершин. В этом цикле пересчета + помечены те клетки, поставка в ктр увелич., и «-» – уменьш-ся. Замечание: иногда д/произвол.означенного цикла вводится понятие оценка цикла – алгебраич.сумма коэф-тов, стоящих в вершинах цикла, взятых с соотв-щими знаками. Д/кажд.свобод.клетки базис.распред-я поставок сущ-ет и при том единствен.цикл пересчета. Причем, операция означивания цикла явл-ся корректной. Т.(о потенциалах): оценка свобод.клетки не измен-ся, если к коэф-там затрат некоторой строки (столбца) таблицы поставок прибавить некоторое число. Изменение коэф-тов затрат можно начинать с любого столбца (строки). Потенциал столбца (строки), избранного д/начала, может быть произвольным. Остальные соотв-но необх-мо пересчитывать.
13. Общий вид задач нелинейного программир-я. Графический метод решения задач нелинейного программир-я.
Во многих эк.моделях исследов-я операций завис-ти между постоянными и перемен.факторами лишь в I приближ-и можно считать лин., более детальное рассмотр-е позволяет обнаружить их нелин-ть. Как пр-ло, такие показ-ли, как прибыль, с/стоим-ть, капитал.затраты на произв-во и др., в действит-ти зависят от объема произв-ва, расхода ресурсов и т.п. нелинейно. К класс.методам оптимизации относ-ся классы Нелин.задач и др. Задачу оптимизации можно сформулировать так: найти переменные х1…хn, удовлетворяющие сис-ме ур-й
кр.мере, частные производные II порядка. #задача Нелин.прогр.: дан.предпр-е д/произв-ва какого-то продукта расходует 2ср-ва в кол-ве х
1 и х2. Это факторы произв-ва (машины и труд), 2различных вида сырья… Факторы машины и труд взаимозаменяемы или в с/хоз-ве взаимоз.факторами считаются посевные площади и кол-во удобрений. Vпроизв-ва, выраженный в натурал.или стоим.ед-цах, явл-ся f-ей затрат произв-ва
1)
3)


