Решим задачу в среде MS Excel. Воспользуемся инструментами «Регрессия» и «Корреляция» надстройки Анализ данных и проанализируем полученные данные. По матрице коэффициентов парной корреляции коэффициент мультиколлинеарности превышает 0,5 (уровень статистической значимости α = 0,05), значит b₁, b₂ и b₃ нельзя интерпретировать как показатели раздельного влияния X₁, X₂ и X₃ на Y. Следовательно, показатель X₃ необходимо исключить из дальнейших расчетов (рисунок Рисунок 1).


Рисунок 1 – Экранная форма расчета (1)
В результате по матрице коэффициентов парной корреляции коэффициент мультиколлинеарности не превышает 0,5 (уровень статистической значимости α = 0,05), значит нет необходимости в устранении мультиколлинеарности. Поэтому возможно использовать множественную регрессию ко всем данным (рисунок Рисунок 2).


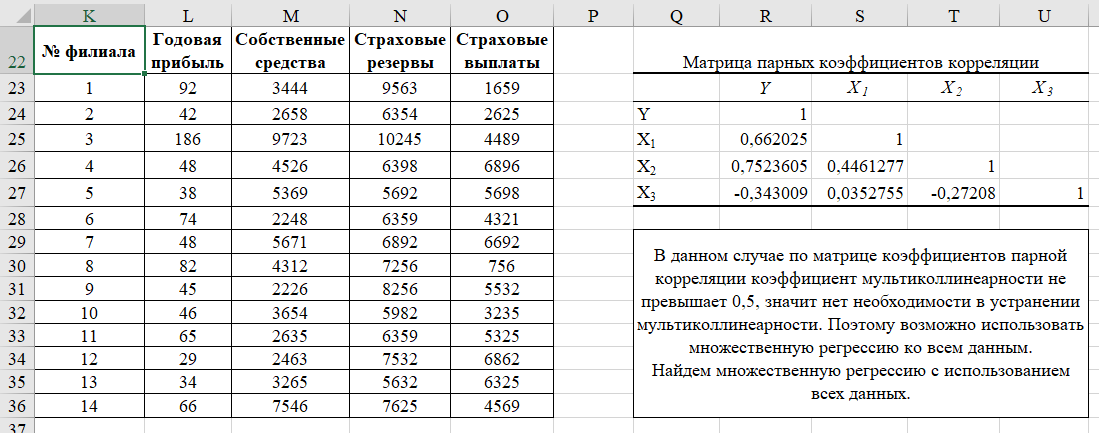
Рисунок 2 - Экранная форма расчета (2)
На основе полученных данных можно записать уравнение множественной регрессии:

Ŷ= -49,4871+0,00819X₁+0,013954X₂-0,0046X₃.

Оценим качество уравнения множественной регрессии с помощью коэффициента детерминации R-квадрат. Исходя из полученных результатов, R-квадрат для множественной регрессии равен 0,7447 (близок к 1). Следовательно, можно утверждать, что уравнение множественной регрессии обладает достаточно высоким качеством. F-критерий Фишера: Fрасч.=9,7219>Fтабл.=3,7083, следовательно уравнение значимо.

Результат расчета представлен на рисунке Рисунок 3.


Рисунок 3 - Экранная форма расчета (3)
Увеличение собственных средств на 1% приведет к увеличению годовой прибыли в среднем на 0,00819 млн руб. Увеличение страховых резервов на 1% приведет к увеличению годовой прибыли в среднем на 0,013954 млн руб. Увеличение страховых выплат на 1% приведет к уменьшению годовой прибыли в среднем на 0,0046 млн руб. 74,47% годовой прибыли объясняется изменением собственных средств, страховых резервов и страховых выплат, на все остальные факторы приходится 25,53%.

Прогнозируется увеличение значения фактора X₂ (страховые резервы) в 1-ом филиале на 10%, что составляет 956,3 млн руб. Увеличим на это число размер страховых резервов в 1-ом филиале: X

---

₂ = 10519,3 млн руб. Оценим размер чистой годовой прибыли данного филиала:

Ŷ(10519,3) = -49,4871+0,00819*3444+0,01395*10519,3-0,0046*1659 = 117,9 млн руб.

Доверительный интервал прогнозируемого индивидуального значения чистой годовой прибыли филиала при уровне статистической значимости α = 0,05:

116,7147<=Y^пр(10519,3)<=119,034.
Пример 2. По 20 предприятиям N-ого региона изучается зависимость выработки продукции на одного работника y (дес.тыс. руб.) от ввода в действие новых основных фондов x₁(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x₂ (%).

№	Y выработка (дес. тыс. руб.)	x1 ввода в действие новых оф (%)	x2 удельный вес рабочих высокой квалификации(%).
1	7	4.3	11
2	7	3.9	13
3	7	3.7	15
4	7	4	17
5	7	4.5	18
6	7	4.8	19
7	8	5.4	19
8	8	4.4	20
9	8	4.9	20
10	10	6.8	21
11	9	6.9	21
12	11	6.4	22
13	9	6.8	22
14	11	7.2	25
15	12	7.1	28
16	12	8.2	29
17	12	8.1	30
18	12	8.5	31
19	14	9.6	32
20	14	9.9	36

---

Построим линейную модель множественной регрессии уравнение множественной регрессии. И найдем коэффициенты парной, частной и множественной корреляции.

Решение

Для начала произведены необходимые расчеты и внесены в таблицу:

№	y	x1	x2	yx1	yx2	x1x2	x1^2	x2^2	y^2
1	7	4.3	11	30.1	77	47.3	18.49	121	49
2	7	3.9	13	27.3	91	50.7	15.21	169	49
3	7	3.7	15	25.9	105	55.5	13.69	225	49
4	7	4	17	28	119	68	16	289	49
5	7	4.5	18	31.5	126	81	20.25	324	49
6	7	4.8	19	33.6	133	91.2	23.04	361	49
7	8	5.4	19	43.2	152	102.6	29.16	361	64
8	8	4.4	20	35.2	160	88	19.36	400	64
9	8	4.9	20	39.2	160	98	24.01	400	64
10	10	6.8	21	68	210	142.8	46.24	441	100
11	9	6.9	21	62.1	189	144.9	47.61	441	81
12	11	6.4	22	70.4	242	140.8	40.96	484	121
13	9	6.8	22	61.2	198	149.6	46.24	484	81
14	11	7.2	25	79.2	275	180	51.84	625	121
15	12	7.1	28	85.2	336	198.8	50.41	784	144
16	12	8.2	29	98.4	348	237.8	67.24	841	144
17	12	8.1	30	97.2	360	243	65.61	900	144
18	12	8.5	31	102	372	263.5	72.25	961	144
19	14	9.6	32	134.4	448	307.2	92.16	1024	196
20	14	9.9	36	138.6	504	356.4	98.01	1296	196
Сумма	192	125.4	449	1290.7	4605	3047.1	857.78	10931	1958
Ср. знач.	9.6	6.27	22.45	64.535	230.25	152.355	42.889	546.55	97.9
Ср. знач^2	92.1	39.31	504.00	4164.7	53015.	23212.0	1839.466	298716.	9584.41

---

Найдем средние квадратические отклонения признаков:

Среднее. квадратичное. отклонение	δy	2.395
	δx1	1.891
	δx2	6.522

Для нахождения параметров линейного уравнения множественной регрессии



необходимо рассчитать неизвестные величины a, b₁, b₂.

Для этого рассчитаем сначала коэффициенты ковариации:

Коэффициенты ковариации	Cov ( y,x1)	4.343
	Сov (y,x2)	14.73
	Сov (x1,x2)	11.59

Затем парные коэффициенты корреляции:

Коэффициенты парной корреляции	ryx1	0.958
	ryx2	0.942
	rx1x2	0.939

Находим коэффициенты чистой регрессии и значение параметра:

Коэффициенты регрессии и параметра а	b1	0.790
	b2	0.131
	a	1.707

Таким образом, получаем следующее уравнение множественной регрессии:



Уравнение регрессии позволяет сделать вывод о том, что при увеличении ввода в действие основных фондов на 1% выработка продукции на одного рабочего увеличивается в среднем на 0,790 дес. тыс. руб., а при увеличении удельного веса рабочих высокой квалификации в общей численности рабочих на 1% выработка продукции на одного рабочего увеличивается в среднем на 0,131 дес. тыс. руб. Далее должна следовать оценка значимости регрессии и коэффициентов регрессии и осуществляться прогноз требуемых показателей [2], [3].

---

3.2. Временные ряды

3.2.1. Задачи анализа временных рядов

Любое предприятие в процессе планирования своей деятельности сталкивается с необходимостью определить тенденции изменения основных экономических показателей.

Задачи анализа временных рядов:

• 
  описание характеристик и закономерностей ряда. На основе этого описания могут быть выявлены свойства соответствующих бизнес-процессов;
  
• 
  моделирование исследуемого процесса;
  
• 
  прогнозирование – предсказание будущих значений временного ряда;
  
• 
  управление. Зная свойства временного ряда можно выработать методы воздействия на соответствующие бизнес-процессы.
  

Если в течение достаточно продолжительного времени регулярно фиксировать курсы валют, акций, цены на товары и т.д., то такие данные образуют временные ряды. Временными рядами являются также данные о выпуске или потреблении различных товаров и услуг по месяцам, кварталам, годам. В производстве временные ряды возникают при измерении количества изделий, выпускаемых подразделениями предприятия за час, смену и т.д., при оценках количества брака за те же периоды, при наблюдении за изменениями запасов на складах.

Практически все временные ряды социально-экономических процессов имеют изменчивый характер, колебания в большей или меньшей мере, что всегда заметно при их графическом представлении.

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Y_t = f(t) +,

 - случайная составляющая,

Y_t - уровень ряда,

f(t) – математическая функция, описывающая закономерность развития явления во времени (тенденцию развития во времени) – употребляют термин «тренд ряда».

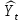- теоретическое значение уровня ряда, соответствующее математической функции тренда.

Поскольку зависимость от времени может принимать разные формы

---

Смотрите также файлы

• Выявление крахмала в йогуртах Выполнена ученицами 9 класса А.pptx

• Содержание детской субкультуры.pptx

• Условия усвоения языка детьми.pptx

• Слайд Тема моего доклада запрет на курение в странах мира.docx

• Программа обучения безопасным методам и приемам выполнения работ повышенной опасности.docx