Cумма	136
Средн.знач	8,5
Var(t)	21,25
Var(y)	4,195
Cov(ty)	4,8375
a	5,365
b	0,227647059

№ квартала(t)	Yt	Si	T+E=Y-S	T	T+S	E=Y-(T+S)	E^2
1	6,00	0,585	5,42	5,59	6,18	-0,18	0,03
2	4,40	-1,98	6,38	5,82	3,84	0,56	0,31
3	5,00	-1,30	6,30	6,05	4,75	0,25	0,06
4	9,00	2,69	6,31	6,28	8,97	0,03	0,00
5	7,20	0,585	6,62	6,50	7,09	0,11	0,01
6	4,80	-1,98	6,78	6,73	4,75	0,05	0,00
7	6,00	-1,30	7,30	6,96	5,66	0,34	0,12
8	10,00	2,69	7,31	7,19	9,88	0,12	0,02
9	8,00	0,585	7,42	7,41	8,00	0,00	0,00
10	5,60	-1,98	7,58	7,64	5,66	-0,06	0,00
11	6,40	-1,30	7,70	7,87	6,57	-0,17	0,03
12	11,00	2,69	8,31	8,10	10,79	0,21	0,05
13	9,00	0,585	8,42	8,32	8,91	0,09	0,01
14	6,60	-1,98	8,58	8,55	6,57	0,03	0,00
15	7,00	-1,30	8,30	8,78	7,48	-0,48	0,23
16	10,80	2,69	8,11	9,01	11,70	-0,90	0,81
136	116,8	-0,02	116,82				1,679

---

Шаг 8. Оценка качества модели.

Сумма квадратов абсолютных ошибок: Σ Е2 = 1,679

Отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения: 2,5%
Вывод: Построенная аддитивная модель объясняет 97,5% общей вариации уровней временного ряда потребления электроэнергии за 16 кварталов исследуемых 4 – х лет и ее можно использовать в прогнозах будущего потребления электроэнергии.


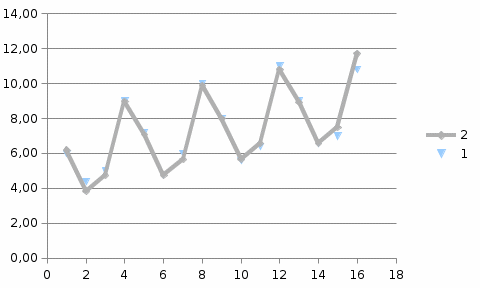
Рис.4. Поквартальное потребление электроэнергии

---

3.3. Дисперсионный анализ информации

Дисперсионный анализ позволяет исследовать различие между группами данных, определять, носят ли эти расхождения случайный характер или вызваны конкретными обстоятельствами. Дисперсионный анализ дает общую схему проверки статистических гипотез, основанную на изучении различных источников вариации, позволяет оценить влияние одного или нескольких факторов на результирующий признак [1], [2].

3.3.1. Однофакторный дисперсионный анализ

Данные для однофакторного дисперсионного анализа − это k независимых выборок из k генеральных совокупностей. Однофакторный дисперсионный анализ сравнивает два источника вариации: между выборками (межгрупповую вариацию) и внутри каждой выборки (внутригрупповую вариацию). Каждая генеральная совокупность подчиняется нормальному распределению, причем стандартные отклонения одинаковы.

Гипотеза Н₀ утверждает, что все средние равны между собой. Альтернативная гипотеза Н₁ говорит о том, что не все средние равны между собой (существуют хотя бы две неравные средние).

Фактор А имеет k уровней. На каждом уровне проводится выборка объемом n_j (j=1,2,…k). Тогда общее число наблюдений n=n₁+n₂+ …+n_k.

Пусть x_ij(i=1,2,…, n_j) −результатыj- той выборки. Рассчитываются:

;

;

.

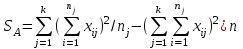А также статистика

.

Доверительная вероятность р, α=1-р. По таблице F- распределения находится граничная точка F_α;k-1;n-k . Если F> F_α;k-1;n-k, то гипотеза Н₀ отклоняется на уровне значимости α.

3.3.2. Примеры к разделу 3.3.

Пример 1. Предприятие минерально-сырьевого комплекса решает вопрос о выборе одной из трех систем контроля качества. Все три системы протестированы. Результаты тестов представлены в табл. 2. Доверительная вероятность

---

р=0,95

Таблица 2

Номер системы	Число выявленных бракованных изделий в партии продукции
1	1, 2, 3, 0, 2, 1
2	2, 3, 1, 0, 1
3	2, 2, 3, 2

Решение:

Проверяется гипотеза об отсутствии влияния различий между системами контроля качества на результат тестирования систем. Предполагается, что выборки получены из независимых нормальных генеральных совокупностей с одинаковой генеральной дисперсией.

Т.к. р=0,95, α=1-0,95=0,05.

Н₀: различия между системами не влияют на результаты тестирования систем.

Н₁: различия между системами влияют на результаты тестирования систем.

Рассчитывается и заполняется табл. 3.

В ней сумма элементов каждой строки второго столбца записывается в третьем столбце, а число элементов в каждой строке второго столбца −в соответствующей строке 4-го столбца. В последней строке рассчитана сумма чисел соответствующего столбца.

Таблица 3

Номер системы	Число бракованных изделий xij	Сумма	nij
1	1, 2, 3, 0, 2, 1	9	6
2	2, 3, 1, 0, 1	7	5
3	2, 2, 3, 2	9	4
Сумма	-	25	15

=

=1²+2²+3²+0²+2²+1²+2²+3²+1²+0²+1²+2²+2²+3²+2²-25²/15≈13,33.

=9²/6+7

---

²/5+9²/4-25²/15≈1,88.

=1,33-1,88=11,45

Статистика =

По таблице F-распределения находится граничная точка F_{0,05;3-1;15-3}= =3,89.

0,99<3,88= F_{0,05;3-1;15-3} , следовательно, принимается гипотеза Н₀ на уровне значимости 5%. Т.е. различия между системами контроля не влияют на результаты тестирования систем. Поэтому можно перейти на более дешевую из трех систему контроля качества.

Рассмотрим на примере следующей задачи некоторые особенности применения пакета программ Excel для исследованиявлияния отдельных качественных факторов на исследуемый признак методом дисперсионного анализа.
Пример 2.

Имеется три организации, на которых внедрены однотипные информационные системы (ИС). В течение шести месяцев определялась стоимость консалтинговых услуг в млн. руб. по сопровождению перечисленных систем. Требуется на уровне значимости α = 0,05 установить наличие зависимости стоимости консалтинговых услуг от варианта информационной системы.

Исходные данные:



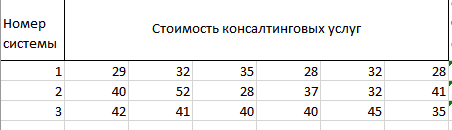
Решение:

1. Внесем исходные данные в таблицу MS Excel


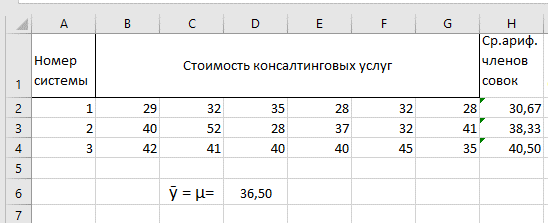
Для исследования модели воспользуемся инструментом «Однофакторный дисперсионный анализ» надстройки MS Excel «Анализ данных».

Укажем входной интервал A1:G4. Укажем, что данные сгруппированы по строкам.



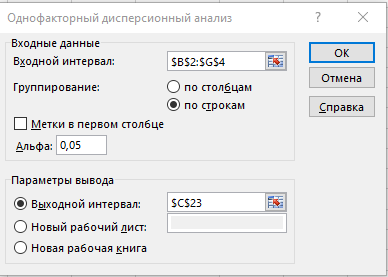
Результаты представлены на рисунке.



Проверка нулевой гипотезы осуществляется на основе критерия Фишера

F_α(m-1, mn-m). В рассматриваемом случае наблюдаемое значение F=5,48, что больше критического значения F_0,05(2,15) = 3,68, которое найдено с помощью функции F.ОБР.ПХ(0,05;2;15).

Таким образом, вариант ИС существенным образом влияет на стоимость консалтинговых услуг по сопровождению указанных систем.

---

Смотрите также файлы

• Выявление крахмала в йогуртах Выполнена ученицами 9 класса А.pptx

• Содержание детской субкультуры.pptx

• Условия усвоения языка детьми.pptx

• Слайд Тема моего доклада запрет на курение в странах мира.docx

• Программа обучения безопасным методам и приемам выполнения работ повышенной опасности.docx