Сабақ №7-8

Педагогтің аты-жөні
Күні:
Сабақ		7-8
Сынып:		Қатысушылар саны: -		Қатыспағандар саны:
Сабақтың тақырыбы		Біреуі біртекті болып келетін екі теңдеу жүйесі
Сабақта қол жеткізетін оқу мақсаты		Екі айнымалысы бар теңдеулер жүйесін шешу арқылы тақырыпты бекіту; қалыптастыру: теңдеу графигін құру және теңдеуді қолдана отырып есептерді шешу деңгейін жоғарылату
Сабақтың мақсаты		Бірі сызықтық, екіншісі екінші дәрежелі болып келетін екі теңдеудің жүйелерін шешу дағдыларына баулу.
Сабақ барысы
Сабақ кезеңдері	Мұғалімнің оқу іс-әрекеті		Білімгердің іс-әрекеті		Бағалау	Ресурстар
Сабақтың басы	Ұйымдастыру кезеңі. білімгерлермен сәлемдесу, түгендеу, сабаққа дайындығын тексеру, назарларын сабаққа аудару. Білімгерлерге сабақтың тақырыбы мен мақсаты хабарланады.		Білімгер сабаққа дайындалады Сабақтың мақсаты мен тақырыбын біледі.
Сабақтың ортасы	Тапсырма №1. Теңдеулер жүйесін шешіңіз 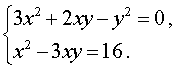Шешім. Біртекті теңдеуді шешейік 3x2 + 2xy – y2 = 0, оны салыстырмалы түрде белгісіз x квадрат теңдеуі ретінде қарастыру: 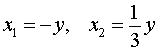X = - y болған жағдайда жүйенің екінші теңдеуінен келесі жүйені аламыз 4y2 = 16, оның түбірі у1 = 2, y2 =– 2 сандары. Осы y мәндерінің әрқайсысы үшін оған сәйкес x мәнін тауып, біз жүйенің екі шешімін аламыз: (– 2; 2), (2; – 2). Жағдайда 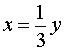, жүйенің екінші теңдеуінен түбірі жоқ келесі жүйені аламыз 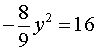Жауабы: (– 2; 2), (2; – 2) Тапсырма №2. Теңдеулер жүйесін шешіңіз. 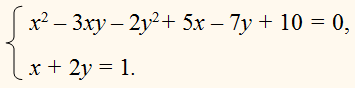Сызықтық теңдеуден өрнектеу х + 2у = 1 айнымалы х арқылы у және өрнек ауыстыру 1 – 2у х орнына жүйенің бірінші теңдеуі, біз түпнұсқаға тең жүйені аламыз (1– 2у)2– 3(1–2у)у – 2у2 + 5(1–2у) – 7у + 10 = 1 – 4у + 4у2– 3у + 6у2– 2у2+5 – 10у – 7у +10 = 8у2– 24у + 16 = 8(у2– 3у + 2). 8(у2– 3у + 2) = 0. 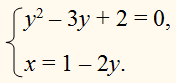Квадрат теңдеуден у2 – 3у + 2 = 0 келесіні табамыз у = 1 және у = 2. Осыдан: 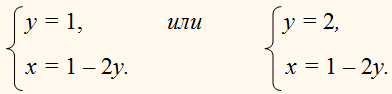Демек, 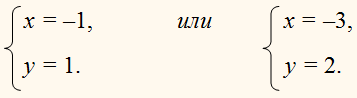Жауабы: (–1; 1), (–3; 2). Алайда, осы түрдегі көптеген жүйелерді басқа жолдармен де шешуге болады. 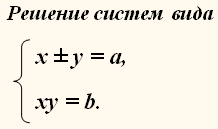Тапсырма №3. Теңдеулер жүйесін шешіңіз. 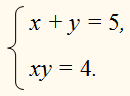X және Y мәндерін квадрат теңдеудің түбірлері ретінде қарастыруға болады: z2 – 5z + 4 = 0. Біз z1 = 1, z2 = 4 аламыз. Жүйенің екі теңдеуі де симметриялы X және Y, сондықтан біз екі жұп шешім аламыз: егер бір шешім болса X1 = 1, Ж1 = 4, содан кейін екіншісі, керісінше, x2 = 4, Ж2 = 1. Тапсырма №4. Теңдеулер жүйесін шешіңіз. 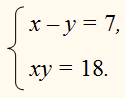Біз жүйені келесідей жазамыз: 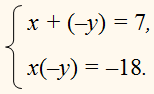Содан кейін X және Y квадрат теңдеудің түбірлері болады: z2 – 7z – 18 = 0. Келесіні аламыз z1 = 9, z2 = –2. Сонда х1 = 9, –у1 = –2, және х1 = 9, у1 = 2 и х2 = –2, –у2 = 9, және х2 = –2, у2 = –9.		Берілген тапсырманы орындайды. Қосымша деректер жинақтайды. Нәтижеге бағытталған білім алады. Берілген тапсырманы орындайды.		ҚБ «Бағдаршам» ҚБ: «Өзін-өзі бағалау» ҚБ «Екі жұлдыз, бір тілек» ҚБ «Бір түйін сөз» әдісі	презентация таратпа материалдар карточкалар интернет ресурстары
Сабақтың соңы 5 мин	Қорытындылау. Бүгінгі сабақтан үйренген жақсы қасиеттерін еске түсіріп, айтып береді.		Сабаққа кері байланыс береді

---

Сабақ №9-10-11

Педагогтің аты-жөні
Күні:
Сабақ		9-10-11
Сынып:		Қатысушылар саны: -		Қатыспағандар саны:
Сабақтың тақырыбы		Теңдеулердің бірі біртекті болатын жүйелерге дейін қысқартылған екі теңдеу жүйелері
Сабақта қол жеткізетін оқу мақсаты		Түбірлер, дәрежелер, логарифмдер, тригонометриялық функциялар және оларды шешу жолдары бар бірнеше белгісіз теңдеулер жүйесін шешуге үйрету
Сабақтың мақсаты		Түбірлер, дәрежелер, логарифмдер, тригонометриялық функциялар және оларды шешу жолдары бар бірнеше белгісіз теңдеулер жүйесін қарастыру
Сабақ барысы
Сабақ кезеңдері	Мұғалімнің оқу іс-әрекеті		Білімгердің іс-әрекеті		Бағалау	Ресурстар
Сабақтың басы	Ұйымдастыру кезеңі. білімгерлермен сәлемдесу, түгендеу, сабаққа дайындығын тексеру, назарларын сабаққа аудару. Білімгерлерге сабақтың тақырыбы мен мақсаты хабарланады.		Білімгер сабаққа дайындалады Сабақтың мақсаты мен тақырыбын біледі.
Сабақтың ортасы	Тапсырма №1. Теңдеулер жүйесін шешіңіз 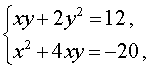Шешім. Жүйе бойынша келесі түрлендірулерді жасайық: жүйенің екінші теңдеуі өзгеріссіз қалады; 5 - ке көбейтілген бірінші теңдеуге 3-ке көбейтілген екінші теңдеуді қосып, жүйенің бірінші теңдеуінің орнына алынған нәтижені жазамыз Нәтижесінде жүйе оған тең жүйеге айналады, онда бірінші теңдеу біртекті теңдеу болады: 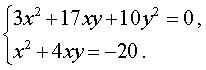Біртекті теңдеуді шешейік 3x2 + 17xy + 10y2 = 0, оны салыстырмалы түрде белгісіз x квадрат теңдеуі ретінде қарастыру: 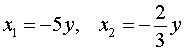X = - 5y болған жағдайда жүйенің екінші теңдеуінен теңдеу аламыз 5y2 = – 20, Түбірі жоқ болған жағдайда , оның түбірі у1 = 3, y2 = – 3 сандары. Осы y мәндерінің әрқайсысы үшін оған сәйкес x мәнін тауып, біз жүйенің екі шешімін аламыз: (– 2; 3),   (2; – 3). Жауабы: (– 2; 3), (2; – 3) Тапсырма №2. Теңдеулер жүйесін шешіңіз: Ауыстыруды жасауға болады и Содан кейін сызықтық теңдеулер жүйесіне өтіңіз: Жүйені қосу арқылы шешуге болады, мысалы. Бірақ біз шешімді ауыстырусыз береміз. Біз жүйенің бірінші теңдеуін 5 – ке, екіншісін 4-ке көбейтеміз және алынған теңдеулерді қосамыз, мысалы, жүйеде бастапқы жүйенің бірінші теңдеуін қалдырамыз. Жауабы: (1;2). Тапсырма №3. Теңдеулер жүйесін шешіңіз: Біз жүйенің бірінші теңдеуінен y+1 өрнектеп, екіншісіне ауыстырамыз. 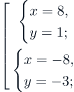Жауабы: (8;1), (-8;-3). Тапсырма №4. Теңдеулер жүйесін шешіңіз: Шешімі: Біз жүйенің теңдеулерін қосамыз, нәтижені теңдеулердің біріне ауыстырамыз, екіншісін қалдырамыз. 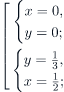Жауабы: Тапсырма №5. Теңдеулер жүйесін шешіңіз: Шешімі: Біз бірінші жолды екіншісіне бөлеміз, жүйеде екінші жолды өзгеріссіз қалдырамыз. Жауабы: (1;2),(8;0,5). Тапсырма №6. Теңдеулер жүйесін шешіңіз: Шешімі:  ретінде ауыстырып, сызықтық теңдеуге шығуға болады Біз шешімді ауыстырусыз береміз. Біз жүйенің екінші теңдеуінен y білдіреміз және біріншісіне ауыстырамыз. Жауабы: (1;-1), (-1;-1).		Берілген тапсырманы орындайды. Қосымша деректер жинақтайды. Нәтижеге бағытталған білім алады. Берілген тапсырманы орындайды.		ҚБ «Бағдаршам» ҚБ: «Өзін-өзі бағалау» ҚБ «Екі жұлдыз, бір тілек» ҚБ «Бір түйін сөз» әдісі	презентация таратпа материалдар карточкалар интернет ресурстары
Сабақтың соңы 5 мин	Қорытындылау. Бүгінгі сабақтан үйренген жақсы қасиеттерін еске түсіріп, айтып береді.		Сабаққа кері байланыс береді

---

Сабақ №12-13

Педагогтің аты-жөні
Күні:
Сабақ		12-13
Сынып:		Қатысушылар саны: -		Қатыспағандар саны:
Сабақтың тақырыбы		Басқа түрлі теңдеулер жүйесін шешудің мысалдары
Сабақта қол жеткізетін оқу мақсаты		Жүйенің барлық теңдеулері үшін жалпы шешімдерді табу немесе шешімнің жоқтығына көз жеткізу
Сабақтың мақсаты		Сызықтық алгебралық теңдеулер жүйесін шешудің әртүрлі тәсілдерін зерттеу
Сабақ барысы
Сабақ кезеңдері	Мұғалімнің оқу іс-әрекеті		Білімгердің іс-әрекеті		Бағалау	Ресурстар
Сабақтың басы	Ұйымдастыру кезеңі. білімгерлермен сәлемдесу, түгендеу, сабаққа дайындығын тексеру, назарларын сабаққа аудару. Білімгерлерге сабақтың тақырыбы мен мақсаты хабарланады.		Білімгер сабаққа дайындалады Сабақтың мақсаты мен тақырыбын біледі.
Сабақтың ортасы	Тапсырма №1. Теңдеулер жүйесін шешіңіз 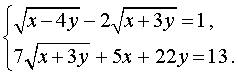Шешім. Формулалар бойынша x және y арқылы өрнектелген жаңа белгісіз u және v енгізейік: 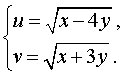Жүйені жаңа белгісіздер арқылы қайта жазу үшін алдымен белгісіз x және y-ді u және v арқылы білдіреміз . Жүйеден мыналар шығады 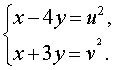Осы жүйенің екінші теңдеуінен x айнымалысын алып тастап, сызықтық жүйені шешейік . Осы мақсатта біз жүйеден келесі түрлендірулерді жасаймыз: жүйенің бірінші теңдеуі өзгеріссіз қалады; екінші теңдеуден бірінші теңдеуді алып тастап, жүйенің екінші теңдеуін алынған айырмашылыққа ауыстырыңыз. Нәтижесінде жүйе оған тең жүйеге айналады 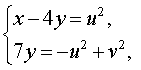біз қайдан табамыз 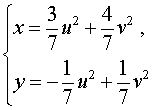Формулаларды қолданып бастапқы жүйені қайта жазайық 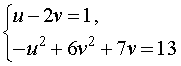Жүйеде бірінші теңдеу сызықтық болып табылады, сондықтан біз одан белгісіз u-ны белгісіз v арқылы білдіріп, осы өрнекті жүйенің екінші теңдеуіне ауыстыра аламыз: Теңдеуді шешу 2v2 + 3v – 14 = 0, Түбірін табамыз Сондықтан жүйенің шешімдері екі жұп сандар болып табылады 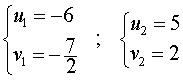Формулалардан мыналар шығады , сондықтан бірінші шешімді алып тастау керек. U жағдайында u2 = 5, v2 = 2 (15) формулалардан x және y мәндерін табамыз :   x = 13,   y = – 3 . Жауабы:   (13 ; – 3) Тапсырма №2. Үш белгісіз екі теңдеу жүйесін шешіңіз 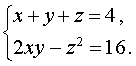Шешім. Жүйеде бірінші теңдеу сызықтық болып табылады, сондықтан біз одан белгісіз z-ді белгісіз x және y арқылы білдіріп, осы өрнекті жүйенің екінші теңдеуіне ауыстыра аламыз: 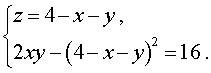Жүйенің екінші теңдеуін басқа түрде қайта жазайық: Кез-келген санның квадраты теріс емес болғандықтан, соңғы теңдікті орындау тек x = 4, y = 4 жағдайында мүмкін болады . Демек, 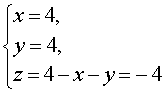Жауабы: (4 ; 4 ; – 4) Тапсырма №3. Теңдеулер жүйесін шешіңіз 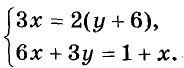Шешім: Осы теңдеулерді сызықтық теңдеулермен ауыстырыңыз, біз жүйені аламыз: 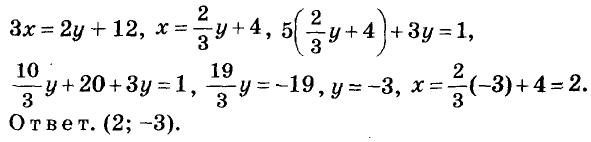Тапсырма №4. Теңдеулер жүйесін шешіңіз: 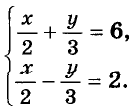Шешім: Екінші теңдеуден бөлшектің мәнін арқылы білдіріп, оны бірінші теңдеуге ауыстырайық. Демек Жауабы. (8; 6).		Берілген тапсырманы орындайды. Қосымша деректер жинақтайды. Нәтижеге бағытталған білім алады. Берілген тапсырманы орындайды.		ҚБ «Бағдаршам» ҚБ: «Өзін-өзі бағалау» ҚБ «Екі жұлдыз, бір тілек» ҚБ «Бір түйін сөз» әдісі	презентация таратпа материалдар карточкалар интернет ресурстары
Сабақтың соңы 5 мин	Қорытындылау. Бүгінгі сабақтан үйренген жақсы қасиеттерін еске түсіріп, айтып береді.		Сабаққа кері байланыс береді

---

Сабақ №14-15

Педагогтің аты-жөні
Күні:
Сабақ		14-15
Сынып:		Қатысушылар саны: -		Қатыспағандар саны:
Сабақтың тақырыбы		Түбірлерді локализациялау
Сабақта қол жеткізетін оқу мақсаты		Сызықтық емес теңдеулердің шешімдері итеративті (тікелей әдістер іргелі математикада жасалады) болып табылатындығын анықтау
Сабақтың мақсаты		F(x) = 0 теңдеуінің нақты түбірлерін шамамен іздеу мәселесі қарастыру
Сабақ барысы
Сабақ кезеңдері	Мұғалімнің оқу іс-әрекеті		Білімгердің іс-әрекеті		Бағалау	Ресурстар
Сабақтың басы	Ұйымдастыру кезеңі. білімгерлермен сәлемдесу, түгендеу, сабаққа дайындығын тексеру, назарларын сабаққа аудару. Білімгерлерге сабақтың тақырыбы мен мақсаты хабарланады.		Білімгер сабаққа дайындалады Сабақтың мақсаты мен тақырыбын біледі.
Сабақтың ортасы	Тапсырма №1. X* = √a түбірін есептеу кезінде итерациялық әдістің конвергенция ретін формула бойынша анықтаңыз 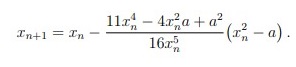Шешімі: Келесі фактіні қолданайық: егер x көпмүшенің k еселігінің түбірі болса Олай болса 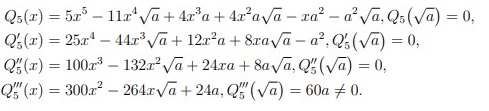Демек сондықтан 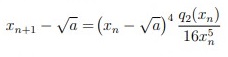яғни, итерациялық әдістің конвергенция реті 4-ке тең. Тапсырма №2. Нақты түбірлерді локализациялау, бастапқы жуықтау нүктесін таңдау, тамырларды нақтылау үшін Ньютон әдісінің итерациялық формуласын жазу, түбірлердің біреуіне әдістің конвергенция шарттарының орындалуын тексеру және берілген дәлдікке қол жеткізуді бағалау. f (x) = sinx − e−x = 0 Шешім: 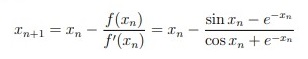Бастапқы жуықтау шартты қанағаттандыруы керек: 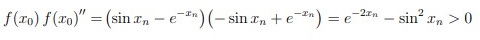f (x0) f (x0)//= (sin xn − e−x ) (-sin xn + e−xn)= e−2xn − sin2 xn>0 Берілген дәлдікке қол жеткізуді бағалау: 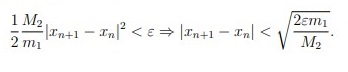Тапсырма №3. X = e2x теңдеуінің түбірлерін оқшаулау үшін қарапайым Итерация әдісін ұсыныңыз- Шешім. Бұл теңдеудің екі түбірі бар x1∈ [−0.8, −0.7], x2*= 0. 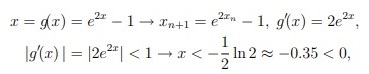яғни, әдіс x*1 маңында жиналады және x * 2 маңында жиналмайды. 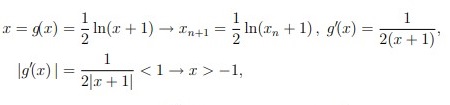яғни, әдіс x*1 маңында да, x*2 маңында да жинақталады. Тапсырма №4. X + LN x = 0 теңдеуінің x* ≈ 0.6 түбірі бар, оны қарапайым Итерация әдістерінің бірімен шешу ұсынылады Осы әдістерді зерттеп, әрқайсысын қолданудың орындылығы туралы қорытынды жасаңыз. Шешімі: 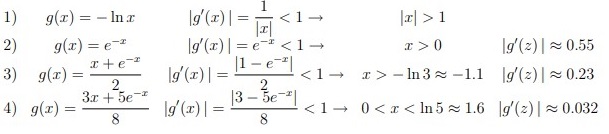яғни, бірінші әдіс есептеу үшін жарамсыз, қалғандарының төртіншісінде конвергенцияның ең жоғары жылдамдығы.		Берілген тапсырманы орындайды. Қосымша деректер жинақтайды. Нәтижеге бағытталған білім алады. Берілген тапсырманы орындайды.		ҚБ «Бағдаршам» ҚБ: «Өзін-өзі бағалау» ҚБ «Екі жұлдыз, бір тілек» ҚБ «Бір түйін сөз» әдісі	презентация таратпа материалдар карточкалар интернет ресурстары
Сабақтың соңы 5 мин	Қорытындылау. Бүгінгі сабақтан үйренген жақсы қасиеттерін еске түсіріп, айтып береді.		Сабаққа кері байланыс береді

---

Сабақ №16-17-18

Педагогтің аты-жөні
Күні:
Сабақ		16-17-18
Сынып:		Қатысушылар саны: -		Қатыспағандар саны:
Сабақтың тақырыбы		Жартылай бөлу әдісі
Сабақта қол жеткізетін оқу мақсаты		Сызықтық емес теңдеулерді шешудің жартылай бөлу әдісін және қадамдық әдісін үйрету
Сабақтың мақсаты		Жартылай бөлу әдісі тақырыбының мазмұнын ашу
Сабақ барысы
Сабақ кезеңдері	Мұғалімнің оқу іс-әрекеті		Білімгердің іс-әрекеті		Бағалау	Ресурстар
Сабақтың басы	Ұйымдастыру кезеңі. білімгерлермен сәлемдесу, түгендеу, сабаққа дайындығын тексеру, назарларын сабаққа аудару. Білімгерлерге сабақтың тақырыбы мен мақсаты хабарланады.		Білімгер сабаққа дайындалады Сабақтың мақсаты мен тақырыбын біледі.
Сабақтың ортасы	Тапсырма №1. Теңдеулерді шешудің қарапайым сандық әдістерінің бірін қарастырайық Теңдеу үшін түбірлік оқшаулау аралығы табылды - [A;b] сегменті. Қажетті түбірді нақтылау үшін [A;b] сегментін екіге бөлеміз және сегменттердің осы бөлінуінен алынған екеуінен біз түбірдің болуы мен бірегейлігі шарттары орындалатын біреуін таңдаймыз (сегменттің соңында функция әртүрлі белгілердің мәндерін алады). Біз сегменттің ортасын формула бойынша табамыз хi=(a+b)/2, i=1,2,3…, біз бұл процесті қажетті дәлдікке жеткенше жалғастырамыз 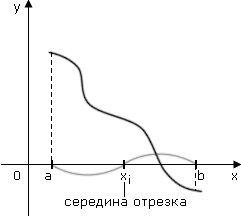Тапсырма №2. Теңдеуді шешу мысалында жартылай бөлу әдісін қолдануды қарастырыңыз х3+x2-1 = 0 сегментте [0;1]. Оқшаулау аралығын екіге бөлейік-бұл нүкте х=0,5. Біз екі кесінді аламыз – [0;0,5] и [0,5;1]. Сегменттердің ұштарындағы функцияның мәндерін есептейік, f(0)=-1<0,f(0,5)=0,53+0,52-1 = 0,125 + 0,25-1=-0,625< 0, f(1)=13+12-1=1+1-1=1>0, яғни сегменттің соңында [0,5;1] функция әр түрлі белгілердің мәндеріне ие, сондықтан теңдеудің түбірі кесіндіге жатады [0,5;1]. Әрі қарай қарау үшін осы сегментті таңдаңыз. Біз жаңа сегмент үшін жартылай бөлу әдісін қайталаймыз. Сегменттің ортасы x=(0,5+1)/2=0,75, алынған екі сегменттің ішінен біз оң жақ сегментті таңдаймыз [0,75;1], демек f(0,75) = -0,015625< 0, f(1)=1> 0. Процесс берілген дәлдік дәрежесімен түбір алғанға дейін жалғасады. Тапсырма №3. Теңдеулерді шешіңіз 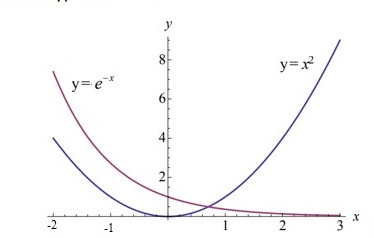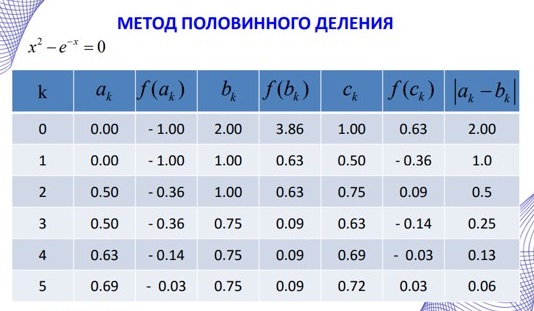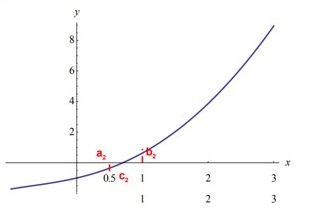Дәлдікпен жуықталған шешім Тапсырма №4. шешімінің түбірін табыңыз [1,3;1,5] сегментте келесі дәлдікпен Е=10-4=0,0001. Шешімі: шешімінің сегментіне жалғыз түбірі бар [1,3;1,5]. 1) Теңдеудің түбірін нақтылайық: [1,3;1,5]: сегменттің ортасын табыңыз 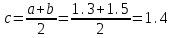. 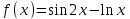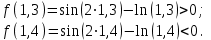Алынған сегменттердің қайсысында екенін анықтайық [1,3;1,4] және [1,4;1,5] функция өзінің белгісін өзгертеді а) [1,3;1,4]: б) [1,4;1,5]: 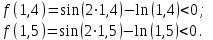Бұл теңдеудің түбірі [1,3;1,4].сегментінде екенін білдіреді Берілген шешімнің дәлдігіне қол жеткізілгенін тексеріңіз 10-4: 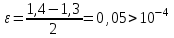, дәлдікке қол жеткізілмейді. 2) Процесті жалғастырыңыз [1,3;1,4] сегментін бөліңіз 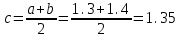. Алынған сегменттердің қайсысында екенін анықтайық [1,3;1,35] немесе [1,35;1,4] функциясы 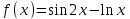белгісін өзгертеді. 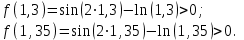1) [1,3;1,35]: 2) [1,35;1,4]: 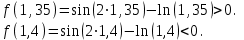Бұл теңдеудің түбірі сегментте екенін білдіреді [1,35;1,4]. Берілген шешімнің дәлдігіне қол жеткізілгенін тексеріңіз 10-4: 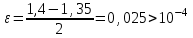, дәлдікке қол жеткізілмейді. 3) Сегментті қайтадан бөліңіз [1,35;1,4] нүктенің жартысы 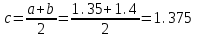. 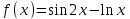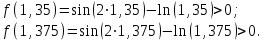Алынған сегменттердің қайсысында екенін анықтайық [1,35;1,375] немес [1,375;1,4] функция өзінің белгісін өзгертеді а) [1,35;1,375]: б)[1,375;1,4]: 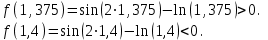Бұл теңдеудің түбірі сегментте екенін білдіреді [1,375;1,4]. Берілген шешімнің дәлдігіне қол жеткізілгенін тексеріңіз 10-4: 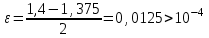, дәлдікке қол жеткізілмейді. 4) Сегментті екіге бөлуді және функция белгілерін жаңа аралықтарда тексеруді жалғастыра отырып, қажетті шешім дәлдігіне жеткенше (өзіңіз жасаңыз), біз аламыз: Теңдеуді дәлдікпен шешу 10-4: х=1,3994.		Берілген тапсырманы орындайды. Қосымша деректер жинақтайды. Нәтижеге бағытталған білім алады. Берілген тапсырманы орындайды.		ҚБ «Бағдаршам» ҚБ: «Өзін-өзі бағалау» ҚБ «Екі жұлдыз, бір тілек» ҚБ «Бір түйін сөз» әдісі	презентация таратпа материалдар карточкалар интернет ресурстары
Сабақтың соңы 5 мин	Қорытындылау. Бүгінгі сабақтан үйренген жақсы қасиеттерін еске түсіріп, айтып береді.		Сабаққа кері байланыс береді

---

Смотрите также файлы

• Задания и задачи.docx

• Лекция по теме 3 Криминалистическая габитоскопия план введение 5 Понятие, содержание и методы габитоскопии.pdf

• Атамасова Ольга Олеговна Герингер Татьяна Сергеевна.docx

• Контрольная работа по английскому языку. Вариант 2 Задание Вставьте нужную форму слова и переведите.doc

• В Номенклатуре должностей медицинских работников и фармацевтических работников психолог, работающий в учреждениях здравоохранения, именуется как.docx