ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1
По исходным данным, представленным в таблице 1, составить два ряда распределения – один дискретный, другой интервальный. По каждому ряду выполнить группировку данных, определить абсолютные, относительные и интегральные частоты, определить средние арифметические и структурные величины, показатели вариации. Сделать обоснованные выводы о качественных особенностях ряда и проиллюстрировать результаты графиками (гистограмма и кумулята для интервального ряда, полигон и кумулята для дискретного ряда). Ручные расчеты дополнить данными, полученными с помощью надстройки «Описательная статистика» пакета Microsoft Excel (Файл – параметры - надстройки – анализ данных – описательная статистика), выявить и пояснить причины расхождения полученных результатов.
Таблица 1 - Данные варианта
| Вариант | Ряд 1 | Ряд 2 | ||
| признак | номера | признак | номера | |
| 1 | Стаж работы | 1-45 | Зарплата за январь | 1-45 |
Таблица 2 - Данные для расчета
| Порядковый номер | Стаж работы | Зарплата за январь | Порядковый номер | Стаж работы | Зарплата за январь |
| 1 | 5 | 27600 | 24 | 3 | 18700 |
| 2 | 3 | 20100 | 25 | 1 | 16300 |
| 3 | 4 | 24400 | 26 | 1 | 16800 |
| 4 | 5 | 25300 | 27 | 4 | 21000 |
| 5 | 3 | 23600 | 28 | 1 | 15100 |
| 6 | 3 | 27100 | 29 | 2 | 13700 |
| 7 | 5 | 21000 | 30 | 2 | 14200 |
| 8 | 5 | 21600 | 31 | 1 | 14500 |
| 9 | 3 | 17800 | 32 | 3 | 18000 |
| 10 | 5 | 21300 | 33 | 5 | 18720 |
| 11 | 4 | 24000 | 34 | 3 | 17440 |
| 12 | 5 | 21800 | 35 | 5 | 20100 |
| 13 | 1 | 22000 | 36 | 3 | 18170 |
| 14 | 2 | 21600 | 37 | 2 | 20260 |
| 15 | 2 | 19400 | 38 | 1 | 14130 |
| 16 | 2 | 17400 | 39 | 3 | 14540 |
| 17 | 4 | 20900 | 40 | 1 | 10470 |
| 18 | 1 | 16300 | 41 | 3 | 14680 |
| 19 | 2 | 14900 | 42 | 3 | 13800 |
| 20 | 3 | 16000 | 43 | 1 | 15400 |
| 21 | 2 | 16200 | 44 | 4 | 27040 |
| 22 | 2 | 17300 | 45 | 2 | 11680 |
| 23 | 2 | 16100 | | | |
Выполнение задания:
Дискретный ряд
1. Ряд 1 – Стаж работы
Сгруппируем данные по стажу работы, определим абсолютные, относительные и интегральные частоты и представим в таблице 1.
Таблица 1 – Сгруппированные данные работников строительного треста по стажу работу
| Стаж работы ,xi | Кол-во рабочих, fi | Накопленная абсолютная частота, S (интегральная) | Удельный вес, % | Накопленная относительная частота S1, %(интегральная) |
| 1 | 9 | 9 | 20,00 | 20,00 |
| 2 | 11 | 20 | 24,44 | 44,44 |
| 3 | 12 | 32 | 26,67 | 71,11 |
| 4 | 5 | 37 | 11,11 | 82,22 |
| 5 | 8 | 45 | 17,78 | 100,00 |
| Итого | 45 | | 100 | |
Для определения средних арифметических и структурных величин, показателей вариации составим расчетную таблицу 2.
Таблица 2 – Расчетные данные
| Стаж работы ,xi | Кол-во рабочих, fi | xi * fi | Накопленная частота, S | |x - xср|*fi | (x - xср)2*fi |
| 1 | 9 | 9 | 9 | 16,4 | 29,884 |
| 2 | 11 | 22 | 20 | 9,044 | 7,437 |
| 3 | 12 | 36 | 32 | 2,133 | 0,379 |
| 4 | 5 | 20 | 37 | 5,889 | 6,936 |
| 5 | 8 | 40 | 45 | 17,422 | 37,942 |
| Итого | 45 | 127 | | 50,889 | 82,578 |
1. Средние показатели
Средняя взвешенная (выборочная средняя)
Мода.
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
Максимальное значение повторений при x = 3 (f = 12). Следовательно, мода равна 3.
Медиана.
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 23. Это значение xi = 3года. Таким образом, медиана равна 3 лет.
Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных.
2. Структурные показатели.
Степень асимметрии.
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии.
As = M3/s3
где M3 - центральный момент третьего порядка.
s - среднеквадратическое отклонение.
M3 = 30.29/45 = 0.67
Положительная величина указывает на наличие правосторонней асимметрии.
Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии:
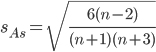
Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/s
As > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным.
Расчет центральных моментов проводим в аналитической таблице 3
Таблица 3- Расчет центральных моментов
| xi | (x - xср)3*fi | (x - xср)4*fi |
| 1 | -54,46 | 99,23 |
| 2 | -6,11 | 5,03 |
| 3 | 0,067 | 0,012 |
| 4 | 8,17 | 9,62 |
| 5 | 82,63 | 179,95 |
| Итого | 30,29 | 293,84 |
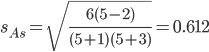
В анализируемом ряду распределения наблюдается несущественная асимметрия (0.271/0.612 = 0.44<3)
Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона:
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Чаще всего эксцесс оценивается с помощью показателя:
Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3.
M4 = 293.84/45 = 6.53
Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом.
Ex < 0 - плосковершинное распределение
Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx
где sEx - средняя квадратическая ошибка коэффициента эксцесса.
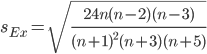
Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным.
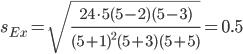
Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным.
