Практическая работа № 2

Тема: Решение алгебраических и трансцендентных уравнений приближенными методами.
Цель: сформировать у студентов, умения и навыки приближенного решения алгебраических и трансцендентных уравнений.
Форма организации занятия – индивидуальная.
Студент должен знать:

- понятия алгебраическое и трансцендентное уравнение ;

- методы приближенного решения уравнений (метод половинного деления, метод хорд, метод касательных).

уметь:

- применять методы приближенного решения уравнений с заданной точностью;

- применять программу Excel для нахождения приближенного решения уравнения.

- применять формулы погрешности элементарных функций.
Содержание отчета о работе:
1. Отчет должен содержать:

- указание темы практической работы;

- цели;

- формулировку задания;

- решение.

2. Вариант определяется согласно контрольному номеру студента по списку.

3. Все задания выполняются письменно, указываются результаты всех промежуточных вычислений (если задание выполнялось в excel, то можно привести скриншот листа excel).

4. При оценивании учитывается правильность и аккуратность выполнения задания.
Пример

Найти корни уравнения с точностью =0.01
Решение методом дихотомии

График функции (рис.1) принимает следующий вид на отрезке [-7;2]:



Рисунок 1. График функции f(x)=x*2x-1

Из него видно, что функция меняет знак на промежутке [0;1].

Разделим этот отрезок на две части и проверим знак функции на концах каждой из них:

f(0)= -1 и f(0,5)=-0,29289; f(0,5)=-0,29289 и f(1)=1.

Отсюда видно, что функция меняет знак на отрезке [0,5;1].

Следовательно, следующим отрезком, который мы станем делить, будет именно он.

Аналогично: f(0,5)= -0,29289 и f(0,75)= 0,261345; f(0,75)= 0,26134 и f(1)= 1.

Корень уравнения принадлежит отрезку [0,5;0,75].

Продолжив итерацию, получим:

f(0,5)= -0,29289 и f(0,625)= -0,03612; f(0,625)= -0,03612 и f(0,75)= 0,26134.

f(0,625)= -0,03612 и f(0,6875)= 0,107212; f(0,6875)= 0,107212 и f(0,75)= 0,26134.

---

f(0,625)= -0,03612 и f(0,6563)= 0,034352; f(0,6563)= 0,034352 и f(0,6875)= 0,107212.

f(0,625)= -0,03612 и f(0,6407)= -0,00109; f(0,6407)= -0,00109 и f(0,6563)=0,034352.

f(0,6407)= -0,00109 и f(0,6485)= 0,016548; f(0,6485)= 0,016548 и f(0,6563)=0,034352.

Длина отрезка [0,6407;0,6485] меньше 2. Значит, корнем уравнения можно считать значение его середины, т.е. 0,6446, т.к. оно удовлетворяет заданной погрешности.
Решение задачи методом хорд

График функции (рис.2) принимает следующий вид на отрезке [-7;2] (с хордой, проходящей через начало координат и пересекающей график в точке (2;7)):



Рисунок 5. График функции f(x)=x*2х-1

Т.к. первая и вторая производные имеют одинаковые знаки, т.е. , то все приближения к корню выполняются со стороны левой границы отрезка и вычисляются по формуле:



Подставив соответствующие значения в эту формулу, получим Х₁:



Аналогично, продолжая итерационный процесс, вычислим последующие приближения, пока результат не удовлетворит заданной погрешности:

             

Соответствие значений функции значениям аргументов представлен в табл.1:

---

Таблица 1.



Из него видно, что значение начинает удовлетворять условию на 10 шаге итерации, т.е. последней результат можно считать ответом к поставленной задаче с допустимой погрешностью, не продолжая вычисления дальше.

Задания для самостоятельного решения

Для заданного уравнения f (x) = 0 найти один из его корней методами дихотомии, и хор; достичь точности 10^–2 методом дихотомии и 10^–3 методом хорд.

Варианты заданий (вариант выбирается по номеру в списке группы)



Приложение

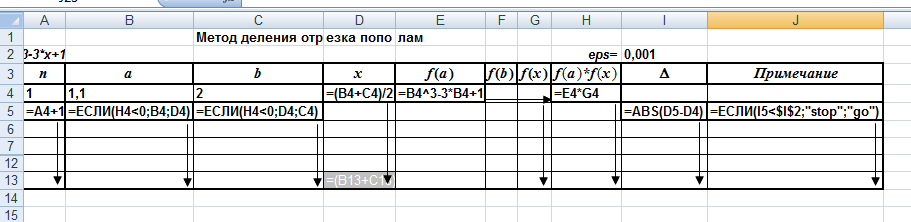
Примеры решения уравнений приближенными методами в excel

		Метод деления отрезка пополам (дихотомии)
x^3-3*x+1=0							eps=		0,001
n	a	b	x	f(a)	f(b)	f(x)	f(a)*f(x)				Примечание
1	1,1000	2,0000	1,5500	-0,9690	3,0000	0,0739	-0,0716
2	1,1000	1,5500	1,3250	-0,9690	0,0739	-0,6488	0,6287		0,2250		go
3	1,3250	1,5500	1,4375	-0,6488	0,0739	-0,3420	0,2219		0,1125		go
4	1,4375	1,5500	1,4938	-0,3420	0,0739	-0,1483	0,0507		0,0562		go
9	1,5289	1,5324	1,5307	-0,0128	0,0013	-0,0057	0,0001		0,0018		go
10	1,5307	1,5324	1,532	-0,0057	0,0013	-0,0022	0,0000		0,0009		stop

---

Метод хорд

---

Смотрите также файлы

• "Schulsystem in Deutschland"Школьное образование в Германии. Эссе должно содержать не менее 10 предложений.docx

• Производственной практики (нужное подчеркнуть) Профессиональный модуль.docx

• Алтын сааматематикалы олимпиадасы20222023оу жылы Ікезе4сынып Атыжні Мектебі Сыныбы Тел нмірі 7 Атаанаызды тел нмірі барлыы 100 пай, уаыты 60 минут.docx

• Некоторые психологические аспекты проведения современной гиа.doc

• Доверительный интервал для доли.docx