Файл: 1 а неопределённость, устранить которую можно путём деления числителя и знаменателя дроби на.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 а) неопределённость
, устранить которую можно путём деления числителя и знаменателя дроби на x в наивысшей степени. В нашем случае будем делить на x2.
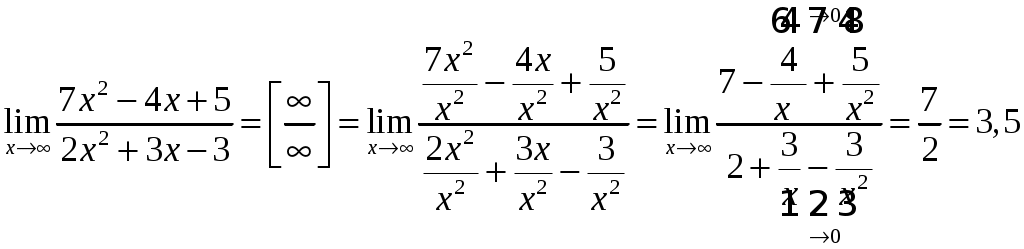
б) При подстановке вместо переменной x её предельного значения 3 получаем неопределенность вида
. Для устранения этого типа неопределённости разложим квадратные трехчлены числителя и знаменателя на множители, воспользовавшись формулой 
, где 
- корни квадратного многочлена.
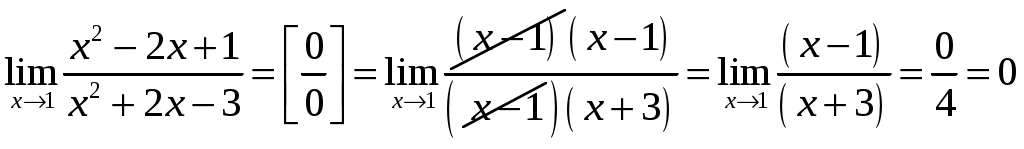
в) Для вычисления предела воспользуемся таблицей эквивалентных бесконечно малых функций при
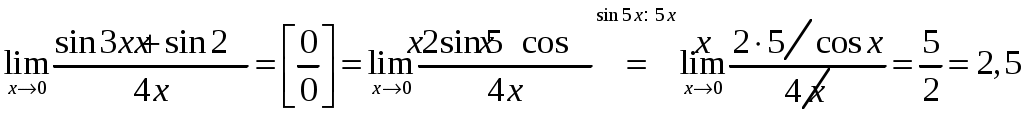
г)
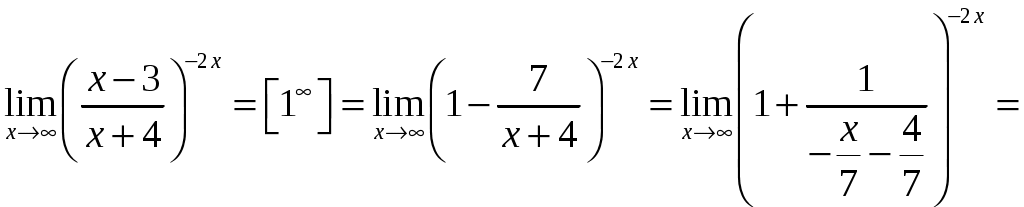
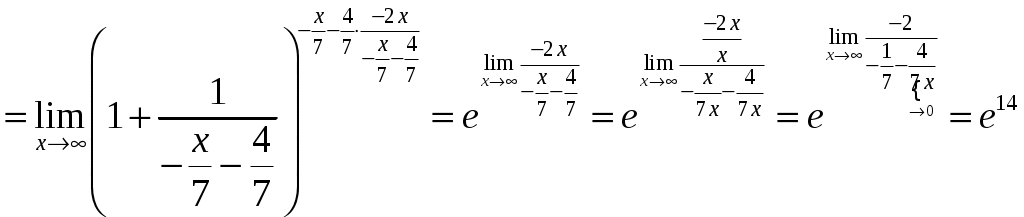
2.
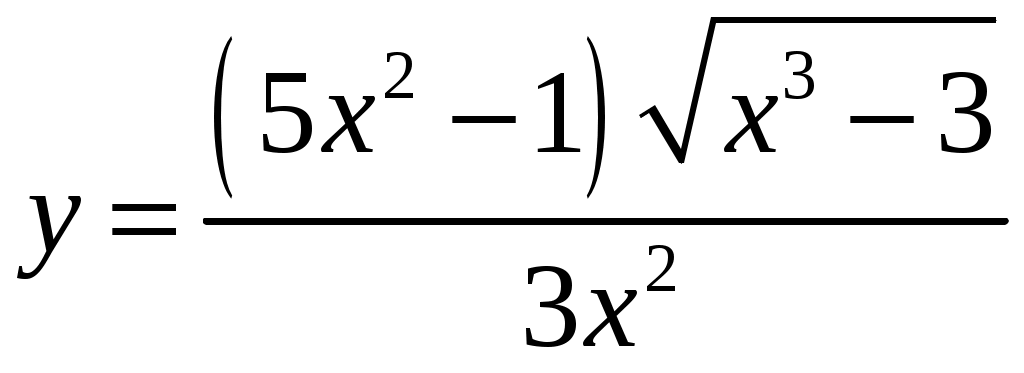
а) Для нахождения производной функции воспользуемся правилом дифференцирования частного и таблицей производных
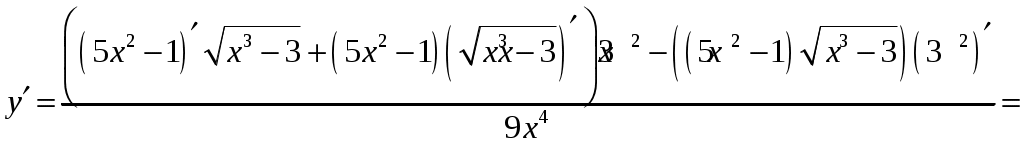
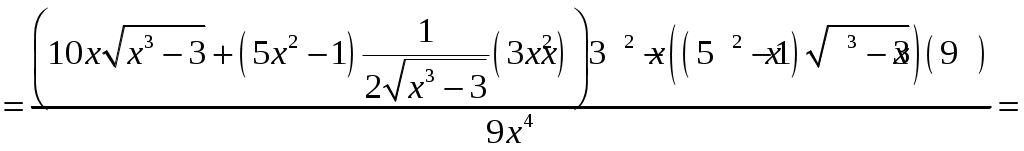
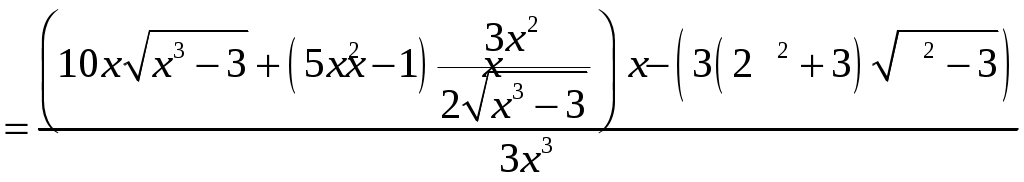
б)
Для нахождения производной функции воспользуемся правилом дифференцирования сложной функции и таблицей производных
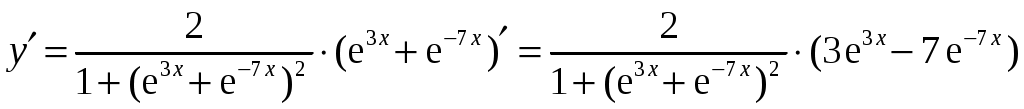
в)
Для нахождения производной функции воспользуемся правилом дифференцирования сложной функции и таблицей производных
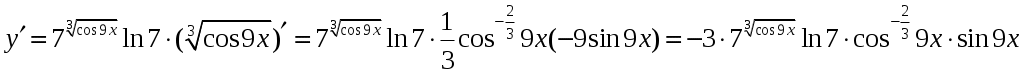
3. 1) Область определения
.2) не является ни нечетной ни четной.
3) Не является периодической, так как имеет конечное число точек разрыва.
4) (0;9/8) – точка пересечения с осями.
5)
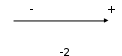
6)
, 
, х= -2 – вертикальная асимптота. 
, 
, 
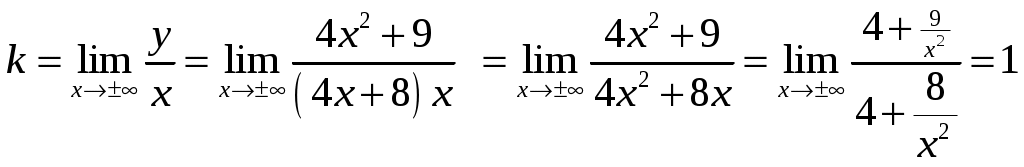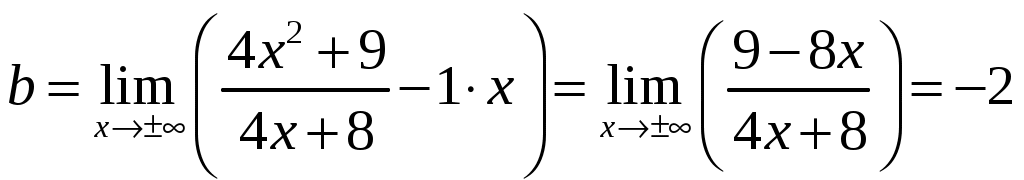- наклонная асимптота.7)
, 
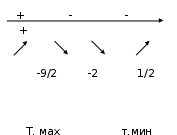
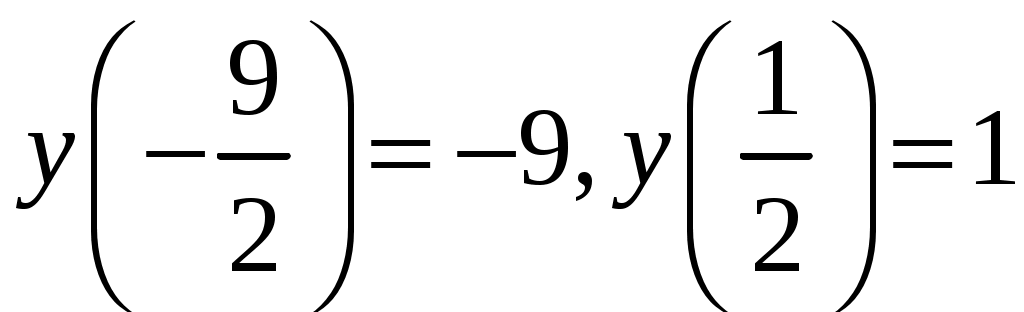
8)
точек нет 
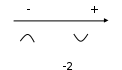
Точек перегиба нет .
9)
.10)
| х | -1 | 1 | 2 | -3 | |
| y | 13/4 | 13/12 | 25/16 | -45/4 | |
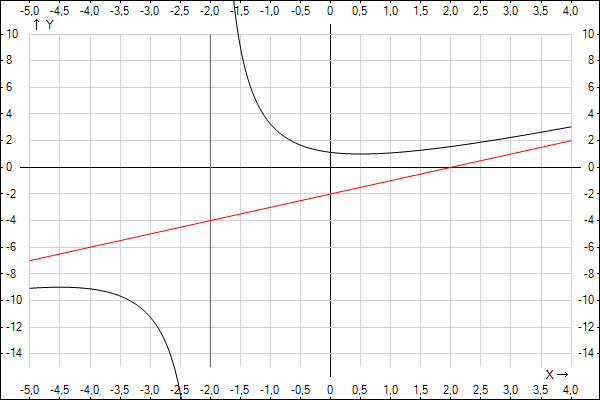
4. a)
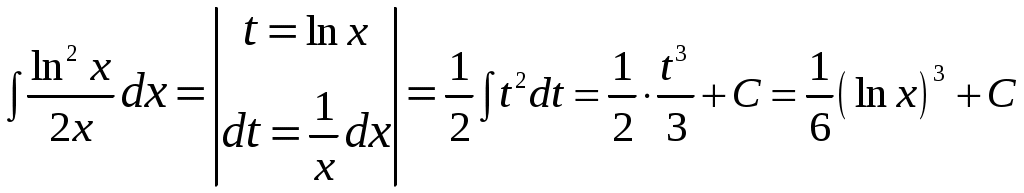
Б) Для вычисления интеграла применим формулу интегрирования по частям:
.
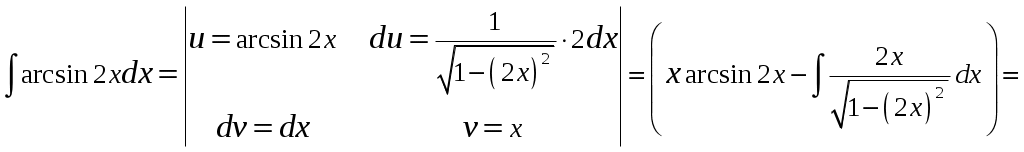
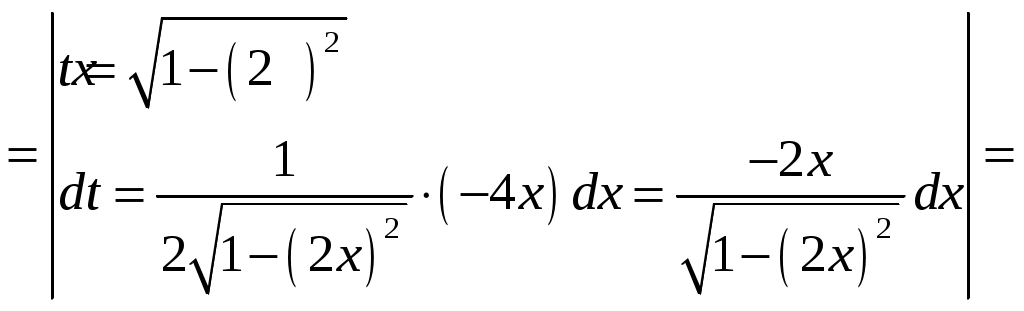
В)
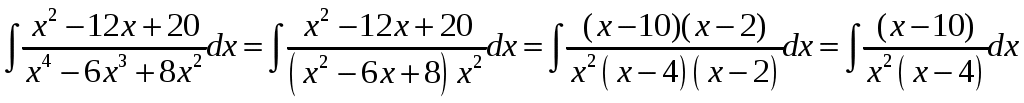
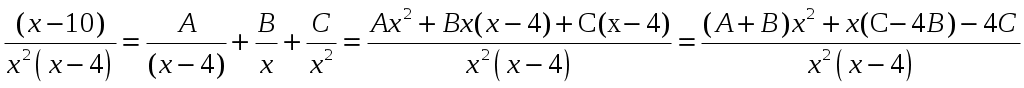
Приравняем коэффициенты при одинаковых степенях х:
=
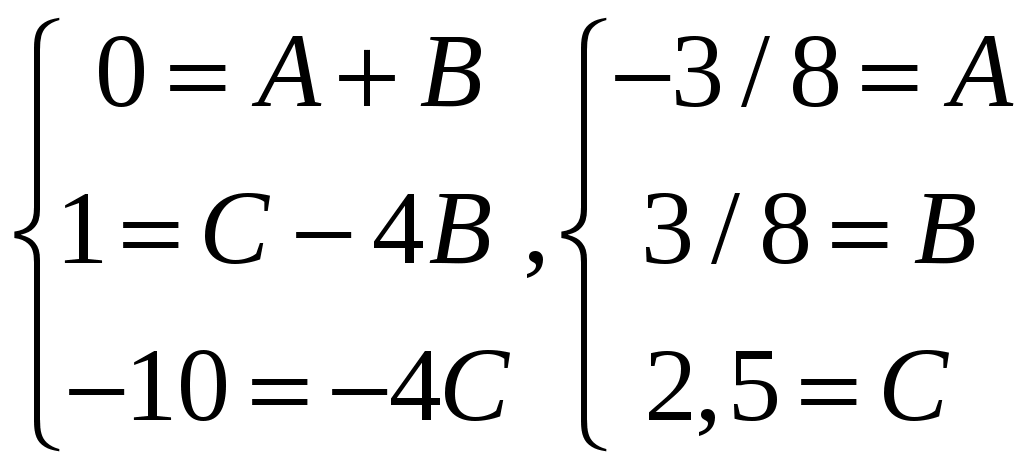
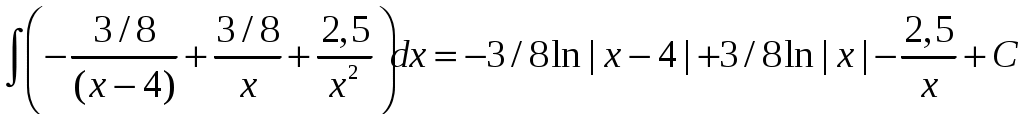
5. Построим графики функций
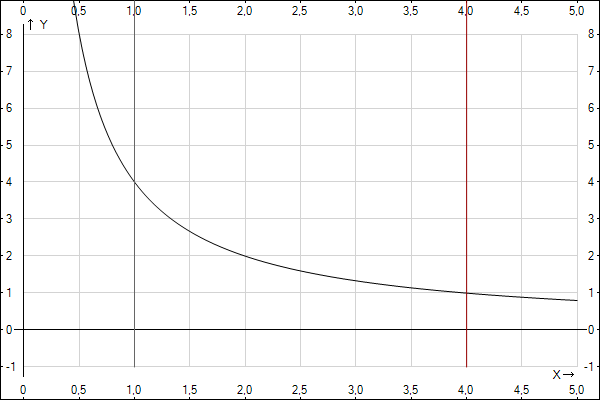
Тогда V=
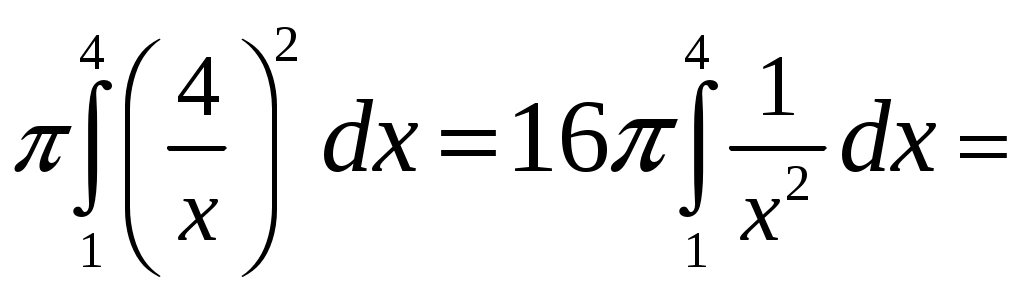
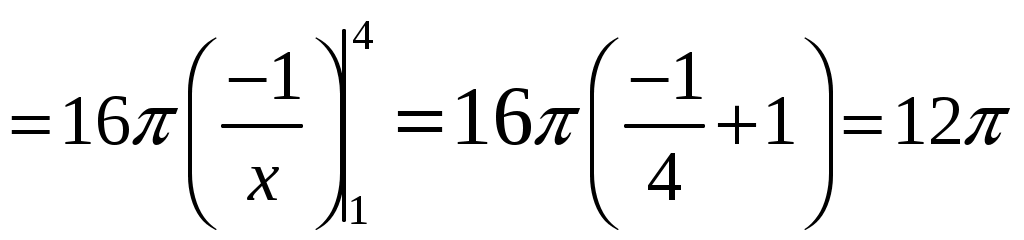.6.
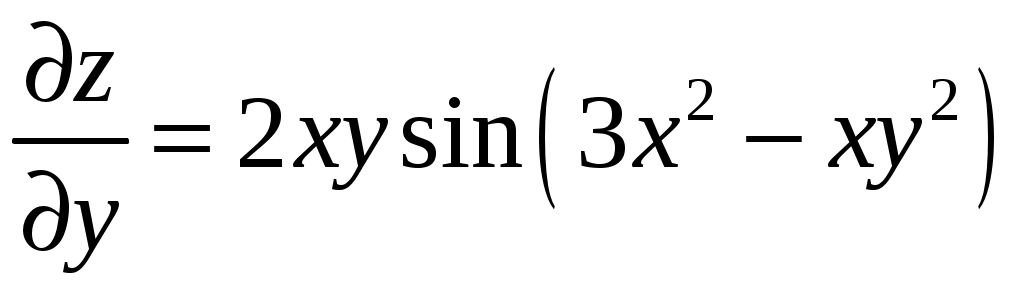
Литература
1. Шипачев В.С. Высшая математика: Учеб. для вузов / В.С. Шипачев. - 6-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для втузов. В 2-х т. Т. 1: - М.: Интеграл - Пресс, 2004. - 416 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 1: Учеб. пособие для втузов. - 5-е изд., испр. - М.: Высш. шк., 1999. - 304 с.
4. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. - М.: Айрис-пресс, 2004.