2.3. Упругие свойства горных пород
Проектирование процессов разработки горных пород в большинстве случаев, так или иначе, связано с определением энергоемкости процесса деформирования и разрушения горных пород. График деформации упругой горной породы может быть представлен в следующем виде (рис. 2.5). Пусть под действием силы Р горная порода деформировалась на величину l. Совершенная при этом работа равна произведению средней силы на величину l:
A = P_срl. (2.14)
Если при деформации сила равномерно изменялась от 0 до Р, то
A = 1/2Pl. (2.15)
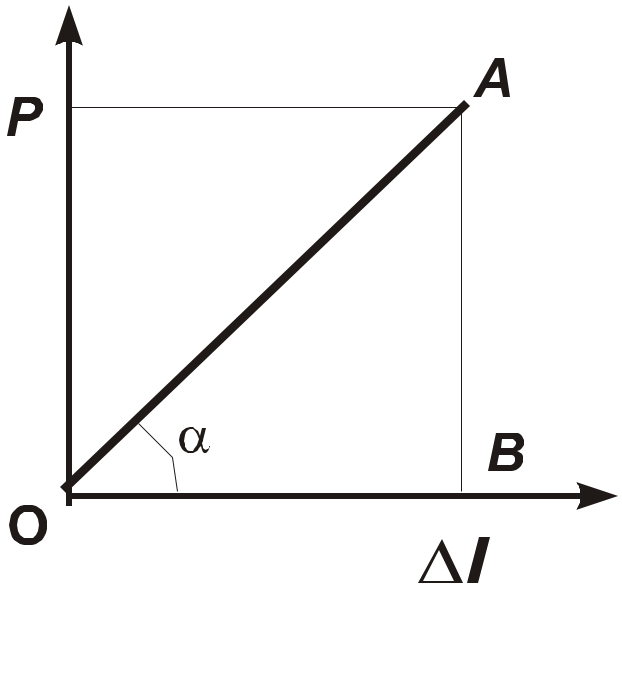Графически эта работа соответствует площади, ограниченной линией деформации, т. е. площади треугольника OAB (см. рис. 2.5). Определим удельную работу деформирования горной породы единичного объема V = Sl, где S- площадь сечения и l - высота куба породы. Тогда
(2.16)

Рис. 2.5. График упругой

деформации

С учетом того, что P/S =  есть напряжение, а l/l =  - относительная продольная деформация, получим:


29

A/V = 1/2, (2.17)
что тоже соответствует площади, ограниченной линией деформации, но в относительных координатах (). При использовании данной формулы возникает проблема измерения деформации . Однако в случае упругого поведения горной породы деформация прямо пропорциональна действующему напряжению. Эта зависимость называется законом Гука:

σ = Е ε. (2.18)

Здесь коэффициент пропорциональности Е, соответствующий тангенсу угла  наклона линии деформации ОА (см. рис. 2.5), называется модулем упругости (модулем Юнга), Н/м² (Па):

Е = σ/ε. (2.19)

Отсюда  = /Е, тогда уравнение (2.16) преобразуется к виду:

(2.20)

Из уравнения (2.19) следует, что модуль упругости есть напряжение, которое нужно приложить к телу для его удлинения в два раза. Для горных пород эта величина составляет десятки миллиардов Паскалей (ГПа). Величина модуля упругости зависит от характера и способа нагружения горной породы. Так, модуль Юнга при сжатии в 1,5 – 4 раза больше по величине, чем при растяжении. При действии касательных напряжений деформация определяется углом сдвига породы δ и закон Гука запишется в виде:

---

τ = Gδ, (2.21)

где G = / называется модулем сдвига. Отсюда следует, что модуль сдвига – это напряжение, необходимое для сдвига породы на 45⁰.

Для каждой горной породы соотношение между продольными и поперечными деформациями – величина постоянная, т.е. является свойством породы. Коэффициент пропорциональности называется коэффициентом Пуассона:

(2.22)

При объемном сжатии коэффициентом пропорциональности между напряжениями и деформациями является модуль объемного (всестороннего) сжатия:

(2.23)

где V/V – относительная объемная деформация.

Для идеально упругого однородного тела между этими характеристиками существует взаимосвязь:
(2.24)

(2.25)
Упругость горных пород в значительной степени определяется их минеральным составом. Основные породообразующие минералы имеют значения модуля Юнга в интервале 20 – 200 ГПа и эта величина возрастает при переходе от кислых пород к основным и ультраосновным, а также с возрастанием плотности пород.
Контрольные вопросы и упражнения
1. Выведите формулы работы упругой деформации. Дайте их графическую интерпретацию.

2. Запишите закон Гука для нормальных и касательных напряжений. Укажите выражения для модуля упругости (Юнга) и модуля сдвига.

3. Что понимается под модулем объемного сжатия? Укажите размерность модулей.


4. Что выражает коэффициент Пуассона горных пород?

5. Определить работу деформирования целика горной породы сечением 1,5х1,5 м и высотой 3 м, если при вертикальном напряжении 25 МПа опускание кровли выработки (деформация целика) составило 30 мм.

6. Определить модуль упругости горной породы для условий предыдущей задачи.

7. Модуль упругости горной породы составляет 35 ГПа и коэффициент Пуассона – 0,25. Вычислить модуль сдвига и модуль объемного сжатия горной породы в Паскалях и кгс/см

---

².

8. Определить удельную работу хрупкого разрушения горной породы, если ее прочность составляет 150 МПа, а модуль упругости – 60 ГПа.

---

Смотрите также файлы

• Тесты по русскому языку.rtf

• Конспект проведения занятий с группой работников 14 караул 44 псч.doc

• Класс 9 Урок 5859 Количество присутствующих Количество отсутствующих Тема Молодость путь в будушее. Цели обучения, которые необходимо достичь на данном уроке.docx

• Фаддеев И.П. Эрозия влажнопаровых турбин.pdf

• Формы, виды и методы обучения персонала в организации по дисциплине.docx