Y_i = a₀ + a₁ x1_i + a₂x2_i+ … + a_mxm_i + E_i (3.20)

В матричной форме записи все соотношения остаются справедливыми, изменяются лишь соотношения для расчета элементов матрицы X. В заключение отметим, что при долговременном прогнозировании предположение о линейности тренда вряд ли справедливо, кривая спроса имеет более сложную форму и не описывается линейной функцией относительно параметров. В этом случае определить аналитически точку минимума квадратичного функционала F(a), обычно уже невозможно. Правда, есть одно важное исключение. Пусть:

Y_i = F(a₀ + a₁ x1_i + a₂x2_i+ … + a_mxm_I)+ E_i (3.21)

и функция G является функцией, обратной к F. Тогда линейная модель по-прежнему имеет место, но уже для преобразованных значений измерений:

G(Y_I )= (a₀ + a₁ x1_i + a₂x2_i+ … + a_mxm_I)+ E_i (3.22)
С точки зрения статистики это преобразование измерений нарушает предположение о нормальном характере поведения измерений. Если закон распределения Y_i был нормальным, то закон распределения G(Y_i) таковым уже не будет. Поэтому найденные оценки лишаются теоретически обоснованного хорошего качества их поведения. На практике же такие процедуры применяют часто.

Но вовсе не обязательно приводить модель к линейной относительно параметров. Она спокойно может оставаться нелинейной, так как существуют хорошо разработанные численные методы. Более того, можно использовать для минимизации функционала средство самого Excel – Поиск решений (Решатель).

Найти минимум функционала не столь сложно - сложнее построить адекватную реальной ситуации модель . Здесь надо выяснить, какие параметры поддаются прямому наблюдению, а какие требуется оценить по результатам наблюдений. Не менее сложно подобрать аналитическое описание с точностью до неизвестных параметров..

Средства Excel, облегчают решение этих задач, а нередко позволяют получить ее решение на основе встроенных стандартных функций.

---

2. Встроенные функции Excel и прогнозирование

Для решения задач прогнозирования в Excel встроены несколько функций. По существу все они сводятся к нахождению оценок по методу наименьших квадратов в задаче линейной регрессии. Наряду с оценками вычисляются и их статистические характеристики, что позволяет строить доверительные интервалы и делать выводы, имеющие вероятностный характер.

2.1. Функция ЛИНЕЙН

В общем случае решает задачу линейной множественной регрессии, вычисляя по методу наименьших квадратов вектор оценок параметров. Используется описанная нами выше модель:

Y = X*a + E (3.23)

Синтаксис вызова этой функции:

ЛИНЕЙН (Известные_значения_Y; Известные_значения_X; Конст; Статистика)

Параметры функции имеют следующий смысл:

• 
  Известные_значения_Y - задает вектор измерений.
  
• 
  Известные_значения_X - в общем случае матрица значений наблюдаемых параметров. Если речь идет о временном тренде, то элементы X задают моменты времени, в которые проводились измерения. Можно опустить X, если значения элементов составляют последовательность 1, 2, 3 и т. д.
  
• 
  Булев параметр "Конст" равен Истина (True), если в линейной записи модели присутствует дополнительно свободный член b, не входящий в вектор параметров a.
  
• 
  Булев параметр "Статистика" равен Истина (True), если наряду с оценками параметров вычисляются и статистические характеристики.
  
• 
  Результат вычислений этой функции - массив, в общем случае состоящий из 5 строк и n+1 столбцов, где n - это размерность вектора искомых параметров a.
  
  • 
    a_n,    a_n-1, …  a₁,  b
    
  • 
    σ_n,    σ_n-1, …  σ₁,  σb
    
  • 
    R*R,   σY
    
  • 
    F,             df
    
  • 
    Ssreg, Ssresid
    
• 
  В первой строке идут оценки параметров a и свободного члена b. Оценки идут в обратном порядке, начиная с a_n. Они и определяют линию регрессии, позволяя рассчитать прогнозируемое значение Y в любой точке, где заданы значения наблюдаемых параметров.
  
• 
  В следующей строке идут среднеквадратические отклонения этих оценок. Выше мы показали, как вычислить полную корреляционную матрицу оценок. Среднеквадратические отклонения являются диагональными элементами этой матрицы. Точнее, на диагонали стоят их квадраты - дисперсии D_I = σ_I * σ_I. Значения σ_I позволяют построить доверительный интервал для соответствующих оценок и вынести суждение об их значимости в линейной модели. Как вычисляются эти значения в Excel, нам осталось непонятно, так как алгоритм не описан. Можно лишь заметить, что применяемый алгоритм не всегда корректен с позиций классической математической статистики.
  

---

Например. Пусть оцениваются два параметра a и b, (Y = a*t +b).

И пусть выполнены всего два измерения - Y1 и Y2. Тогда, каковы бы ни были ошибки в измерениях, линия регрессии пройдет через две наблюдаемые точки. Excel скажет, что ошибок в оценках параметров нет, и выдаст значения σ₁ и σ₂ , равные 0, хотя ясно, что это не так.

Коэффициент детерминации R² имеет значение в интервале от 0 до 1 и позволяет оценить, насколько хорошо сглаживаются измеренные значения линией регрессии. Он равен 1, если линия регрессии проходит через все измеренные точки. При этом можно полагать, что есть строгая функциональная зависимость между измеряемым значением Y и параметрами a_i. Предыдущий пример показывает, что недостаточное количество измерений может приводить к такому же результату. Поэтому и к этому параметру надо относиться с осторожностью. Вычисляется коэффициент детерминации по формуле:

R² = D_reg / D (3.24)
и представляет отношение дисперсии, объясняемой регрессией, к общей дисперсии. О смысле этих терминов чуть ниже.

Вы должны знать ,что означают и как используются параметры σ_Y, F и число степеней свободы df.

Последние два значения - Ssreg и Ssresid задают дисперсию, объясняемую регрессией, и остаточную дисперсию, представляющую разность между общей дисперсией и D_reg. Обе дисперсии вычисляются "обычным" способом:
D = (Y_I - E)² ; D_reg = (Y_I - E)² , (3.25)
где E - среднее значение измеренных значений, а Y_I - сглаженные значения, вычисленные из уравнения регрессии.

Итак, для решения задач прогнозирования функция ЛИНЕЙН позволяет построить уравнение регрессии, как для временных рядов, так и в общем случае линейной множественной регрессии, когда наблюдается несколько параметров.

---

Пример выполнения задачи прогнозирования

Прогноз произведем на основании уравнения регрессии (применения функции ЛИНЕЙН в задаче прогнозирования)

1-способ
Менеджер условного офиса решил построить регрессионное уравнение (модель), прогнозирующее продажи одной из книг. В его распоряжении были данные по продажам этой книги за последние 10 недель. Агенты офиса фиксировали также уровень рекламы и количество конкурирующих товаров (книг на аналогичную тему). Используя функцию ЛИНЕЙН, менеджер построил уравнение множественной регрессии. На рис.3.1 показан лист рабочей книги Excel, где размещены данные о продажах и где построено уравнение регрессии, основываясь на этих данных:

Примечание: Формулу необходимо ввести как формулу массива в первую ячейку. Потом выделяется весь диапазон, нажимается F2, а затем Ctrl+Shift+Enter.

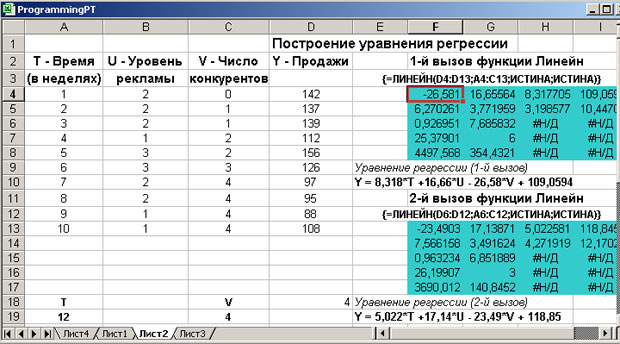
Рис. 3.1.  Построение уравнения регрессии по данным продаж
Менеджер построил это уравнение дважды, получив два уравнения - Y1 и Y2, используя выборки измерений разного объема (см. данные на рис.). Этот полезный прием позволяет понять, насколько полученные коэффициенты критичны к измерениям.

Менеджер достаточно тщательно проанализировал все данные, возвращаемые функцией ЛИНЕЙН для двух ее вызовов. Обратите внимание, массивы результатов работы функции на рисунке 3.1 подсвечены.

С содержательной точки зрения важен следующий полученный результат. Оба измеряемых параметра - уровень рекламы и число конкурирующих книг - являются статистически значимыми. Большее влияние на уровень продаж оказывает число книг - конкурентов.

Менеджер решил использовать полученные уравнения как для прогноза будущих продаж, так и для принятия таких решений, как, скажем, повышение уровня рекламы. Чтобы визуально увидеть влияние уровня рекламы на продажи, менеджер использовал полученные уравнения для построения графиков Y1(U) и Y2(U) при фиксированных значениях параметров T и V. Результаты работы можно увидеть на рисунке 3.2.

---

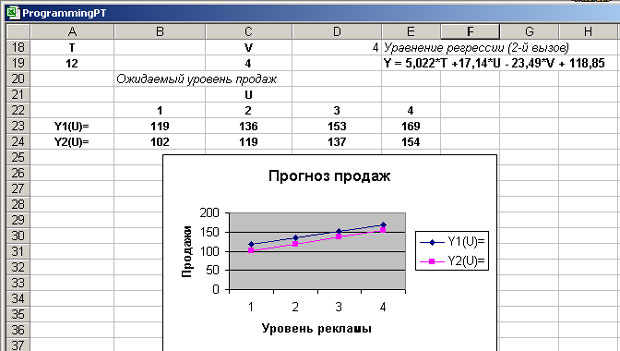
Рис. 3.2.  Прогнозирование продаж в зависимости от уровня рекламы
Полученные графики наглядно показывают, что при переходе от первого уровня рекламы к четвертому можно в полтора раза повысить продажу книг. Это предложение экономически целесообразно и менеджер представил его для принятия решений руководителю организации.
2- способ построения регрессии с использованием раздела меню Сервис – Анализ данных. Выполнить самостоятельно!

2.2. Функция ТЕНДЕНЦИЯ

В основе всех других функций Excel, используемых для прогноза и регрессионного анализа лежит функция ЛИНЕЙН. Так, если уравнение регрессии уже построено, вычислить значение в новой точке нетрудно. Функция ТЕНДЕНЦИЯ решает эту простую задачу. Она неявно вызывает функцию ЛИНЕЙН и, используя полученные оценки параметров, вычисляет прогнозируемые значения в новых точках. Обращение к ней имеет вид:

ТЕНДЕНЦИЯ (Известные_У, Ивестные_Х, Новые значения_Х, Конст)

Здесь мы видим один новый параметр, задающий в общем случае матрицу новых значений Х. Все остальные параметры имеют тот же смысл, что и функции ЛИНЕЙН. В результате возвращается вектор прогнозных значений У, вычисленный в точках, заданных матрицей новых значений Х. Каждая ее строка задает одну точку.

2.3. Функция ПРЕДСКАЗ

- частный случай функции ТЕНДЕНЦИЯ - используется в линейной модели с двумя параметрами, когда уравнение регрессии имеет вид:

y = a*x + b (3.26)

В этом случае Y и X представляют одномерные массивы данных. Вызов функции таков:

ПРЕДСКАЗ( x; Известные_Y; Известные_X)

Здесь x - точка, для которой строится прогноз.

ЛГРФПРБЛ_Построение_нелинейного_уравнения_регрессии'>2.4. Функция ЛГРФПРБЛ

Построение нелинейного уравнения регрессии, которое простым преобразованием сводится к задаче линейной регрессии. Такое преобразование осуществляет функция

---

Смотрите также файлы

• Русский язык 4 класс 1 четверть сор2.docx

• Карточка 2 Ттікті сйектер атаыз Жамбас белдеуі мен ая сйектері атаыз озалмайтын сйектерге андай сйектер жатады, андай байланыспен байланысан Карточка 3.docx

• Пояснительная записка Программа воспитательной работы в 11 классе составлена на основе методических рекомендаций.docx

• Установление происхождения детей.docx

• Конкурсе Битва первокурсников Колледжа АлтГУ.docx