Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»

Реферат

Дисциплина: «Высшая математика»

Тема: «Прямая на плоскости и в пространстве»

Выполнила: Храмикова Диана Станиславовна

Группа: ГМН 1121(2)

Омск

2022 г.

Содержание

Введение……………………………………………………………………3

Раздел 1. Прямая на плоскости и в пространстве: теоретические основы…………………………………………………………………………...4

Раздел 2. Методология решения задач………………………………...13

Раздел 3. Практика применения прямой на плоскости и в пространстве в экономике…………………………………………………………………… 16

Заключение……………………………………………………………...22

Список литературы……………………………………………………. 23

Введение

Необходимость изучения основ аналитической геометрии, в частности прямой на плоскости и в пространстве, продиктована широким использованием математических методов в современной экономической практике. Знание основ делает возможным изучение прикладных и экономических наук.

Изучение прямых на плоскости и в пространстве сопровождается решением большого количества задач, среди которых особое место занимают задачи на доказательство и задачи конструктивного характера. Конструктивные задачи трехмерного пространства требуют как формально -логического подхода при их решении, так и знания проекционного чертежа (параллельного проектирования и его свойств).

Объект исследования в данной работе - геометрический элемент – прямая.

Цель работы состоит в изучении методов исследования прямой на плоскости и в пространстве, а также практики их применения.

В соответствии с поставленной целью в работе необходимо решить следующие задачи:

1) рассмотреть основные способы задания прямой на плоскости и в пространстве;

2) изучить задачи на взаимное расположение прямых в пространстве;

3) исследовать практический опыт применения прямой на плоскости и в пространстве в экономике.

В работе используются следующие методы: метод координат, метод визуализации данных (функции, графики).

Теоретическую и методологическую основу работы составляют труды отечественных и иностранных ученых по данному вопросу.

Раздел 1. Прямая на плоскости и в пространстве: теоретические основы

---

В аналитической геометрии, как и во всей математике существуют основные понятия, с которых все начинается. Основные понятия не определяются. Считается, что в каждом из нас существуют интуитивные представления о них. В этих интуитивных представлениях собран исторический опыт человечества в области математических знаний. Одним из таких основных понятий для нас является прямая.

Понятия точки, прямой и плоскости в геометрии Евклида первичны и потому - неопределяемы. Аналитическая геометрия дает определение этих понятий (как множеств решений тех или иных уравнений), но никакого чуда при этом не происходит - первичные понятия отодвигаются в другую область¹.

Многие авторы учебных пособий начинают рассмотрение темы с декартовой системы координат на плоскости. Например, О.В. Воробейчикова, С.И.Колесникова² дают следующее определение уравнения линии:

Уравнение 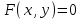называется уравнением линии 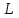относительно заданной системы координат, если этому уравнению удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты ни одной из точек, не лежащей на ней. Линию 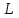еще называют кривой, а ее уравнение – уравнением в общем виде или в неявной форме.

Затем авторы приводят примеры линий:

1) 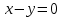. Этому уравнению удовлетворяют точки, у которых абсцисса равна ординате, то есть данное уравнение описывает биссектрису I и III квадрантов (Рис. 1.1).

2) 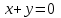. Данное уравнение описывает биссектрису II и IV квадрантов (Рис. 1.1.).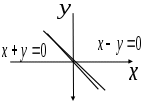



Рис. 1.1. Биссектрисы I и III квадрантов, II и IV квадрантов
Интуиция: прямая на плоскости однозначно задаётся если известны:

1. 
   точка ????_????(????_????,????_????), через которую проходит прямая
   
2. 
   и «направление, привязанное к прямой», что задавалось несколькими способами; в зависимости от конкретики - разные уравнения (но все они первого порядка).
   

Разнообразие видов уравнений прямых порождается многообразием геометрических способов их задания. По любому набору геометрических данных, однозначно определяющих прямую, можно составить уравнение этой прямой

---

, причем геометрические данные будут отражены в коэффициентах уравнения. И наоборот, коэффициенты любого уравнения прямой имеют геометрический смысл, соответствующий способу задания прямой.

Исследователи (О.В. Воробейчикова, С.И.Колесникова³, Колодко Л.С.⁴, Логинов А.С.⁵, Ерусалимский Я.М., Чернявская И.А.⁶, Булатова М.Г. ⁷, С.Н. Кузнецова, М.В. Лукина⁸) приводят различные формы уравнения прямой на плоскости:

1. 
   уравнение прямой через ее нормаль
   

2. 
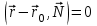
   общее уравнение прямой: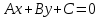
   
3. 
   параметрическое уравнение прямой: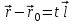
   
4. 
   каноническое уравнение прямой:
   

.
уравнение прямой с угловым коэффициентом, которое позволяет определить всякую прямую, расположенную под углом, относительно исходной. ,

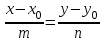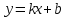где 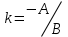, 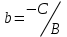при 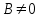. Коэффициент 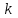– есть тангенс угла наклона прямой к оси 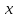(Рис. 1.2.), 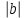– ордината точки пересечения прямой с осью .



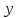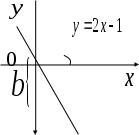
Рис. 1.2. Коэффициент 2 – есть тангенс угла наклона прямой к оси
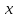
Или в виде:

.

( 2.0 )

---

6. 
   уравнение прямой в отрезках:
   

.

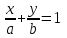( 2.0 )

В дополнение к общему уравнению прямой некоторые исследователи (Логинов А.С.⁹) отмечают одно важное свойство общего уравнения прямой.

Отложим вектор нормали из какой-нибудь точки прямой, заданной уравнением Ax+By+C=0. Пусть M(x;y) - какая либо точка плоскости, тогда

1) если Ax+By+C>0, то точка M(x;y) лежит с той же стороны от прямой, что и вершина вектора ;

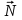2) если Ax+By+C<0, то точка M(x;y) и вершина 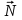лежат с разных сторон от прямой;

3) если Ax+By+C=0, то точка M(x;y) принадлежит прямой (рис. 1.3)


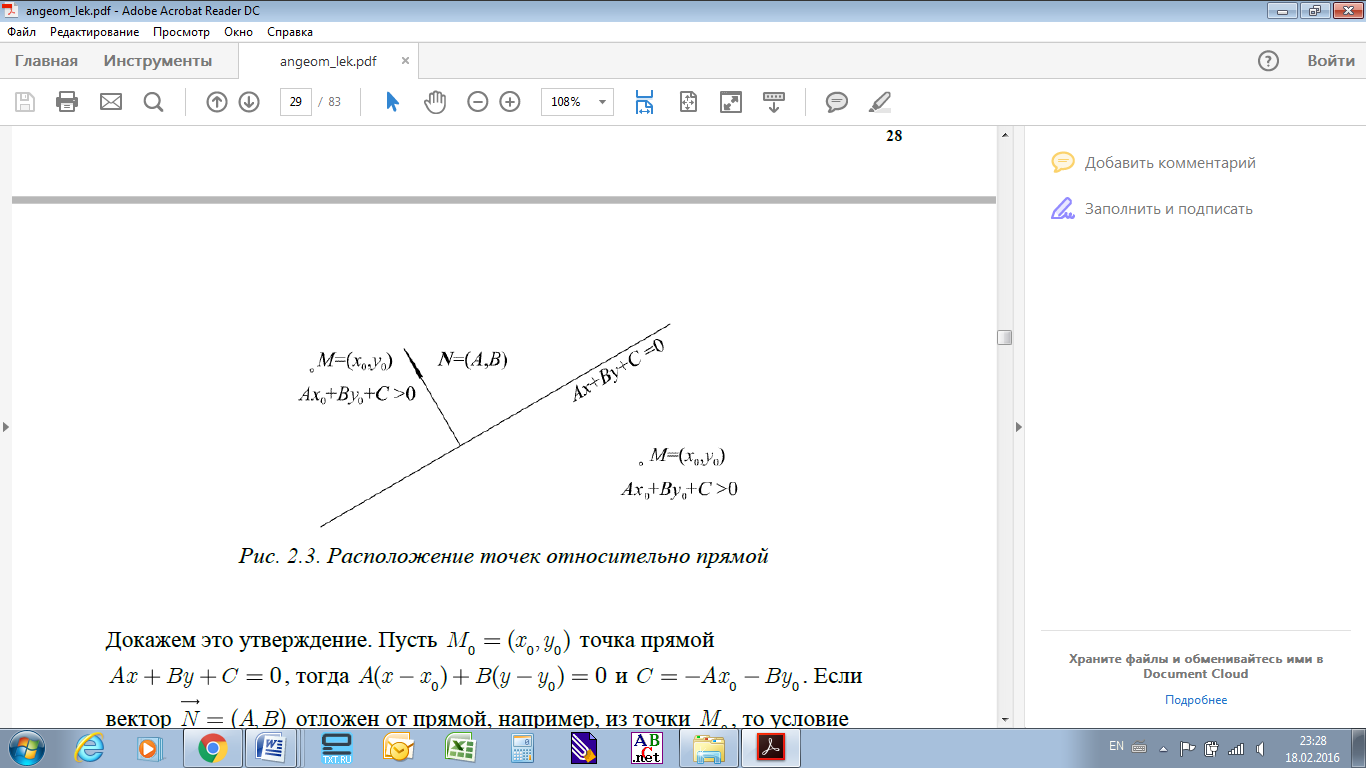
Рис 1.3. Расположение точек относительно прямой

Автор также отмечает, что с помощью нормального уравнения прямой определяют расстояние от точек до прямых, а именно:

Расстояние от точки M₁(x₁;y₁) до прямой Ax+By+C=0 с нормальным уравнением равно



Другие авторы (Ерусалимский Я.М.,Чернявская И.А. ¹⁰) добавляют следствия теоремы уравнения прямой с угловым коэффициентом.

Следствие 1. (Условие совпадения прямых).

Две прямые l₁ : y =k₁x + b₁ и l2 : y = k₂x + b₂ совпадают тогда и только тогда, когда k₁ = k₂ и b₁ = b₂.

Следствие 2. (Условие параллельности прямых).

Две прямые l₁ :y = k₁x + b₁ и l₂ : y = k₂x + b₂ параллельны тогда и только тогда, когда k₁ = k₂ и b₁ = b₂.

Следствие 3. (Условие перпендикулярности прямых).

Две прямые l₁ : y =k₁x + b₁ и l2 : y = k₂x + b₂ перпендикулярны тогда и только тогда, когда k₁ · k₂ = −1.

Ерусалимский Я.М., Чернявская И.А. также рассматривают уравнение прямой, проходящей через заданную точку и имеющей заданный угловой коэффициент:

Дано: k — угловой коэффициент прямой l и точка M(xM, yM) ∈l. Требуется найти уравнение прямой l.

Уравнение прямой

---

l с угловым коэффициентом k имеет вид y = kx + b, b определяется, исходя из условия, что M ∈l. Следовательно, y_M= kx_M+ b, тогда b = y_M− kx_M. Подставляя это значение в исходное уравнение прямой l, выводится уравнение прямой, проходящей через заданную точку и имеющей заданный угловой коэффициент :

y = kx + (y_M− kx_M) или y − y_M= k(x − x_M).

А. E. Умнов¹¹ задается вопросом: каждое линейное уравнение в декартовой системе координат на плоскости задает некоторую конкретную прямую, но, с другой стороны, конкретная прямая на плоскости может быть задана бесчисленным множеством линейных уравнений и естественно возникает вопрос: при каких условиях два разных линейных уравнения задают одну и ту же прямую?

В качестве ответа на вопрос доказывает теорему:

Для того чтобы уравнения

A₁x+ B₁y+ C₁= 0 │A₁│ + │B₁│ > 0 и

А₂ x+ B₂y+ C₂= 0 │A₂│ + │B₂│> 0

были уравнениями одной и той же прямой, необходимо и достаточно, чтобы существовало число 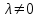, такое, что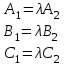



Автор отмечает, что уравнение прямой не в любой системе координат является алгебраическим уравнением первой степени. Например, в полярной системе координат оно может иметь вид



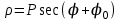
Угол  между прямыми исследователи (Колодко Л.С.¹², О.В. Воробейчикова, С.И.Колесникова¹³) предлагают находить, используя направляющие векторы, векторы нормалей или угловые коэффициенты прямых.

В случае, если прямые L₁ и L₂ заданы каноническими уравнениями:

L₁: 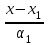= 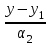, 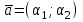— направляющий вектор,

L₂:

---

Смотрите также файлы

• Отчет по производственной (преддипломной) практике специальность 40. 02. 02 Правоохранительная деятельность.docx

• 1. Общая характеристика ооо Тандер 3.docx

• Выполните письменные задания 1 и 2 по дисциплине.odt

• Решение Qтр.SпожJтр6000,0848лс Nгпс600 Qтр qгпс486 8гпс600 Nгпс2000 Qтр qгпс4820 3гпс2000.docx

• Практическая работа 3 11 класс Сравнение экономики двух зон Китая Западной и Восточной. Цель работы.docx