Добавлен: 11.04.2024
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 
, 
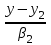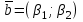— направляющий вектор,
авторы отмечают, что угол между направляющими векторами равен углу или смежному с ним тупому углу , поскольку эти векторы направлены параллельно прямым. Так как
cos () = cos , то cos =cos () . Поэтому
cos =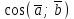 
= 
= 
.
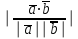В случае, если прямые L1 и L2 заданы своими общими уравнениями:
L1: A 1 x + B 1 y + C 1 = 0,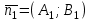
— вектор нормали,
L2: A 2 x + B 2 y + C 2 = 0,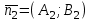
, — вектор нормали,
угол между векторами нормалей равен углу или смежному с ним тупому углу , поскольку эти векторы направлены перпендикулярно прямым. Тогда
cos = cos () =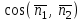 
= 
= 
.
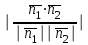В случае, если прямые L1 и L2 заданы уравнениями
y = k 1 x + b1 и y = k2 x + b2
с углами 1 и 2 между прямыми L1 и L2 и осью ОХ, то
угол между L1 и L2 равен 1 – 2 или 2 – 1. Поэтому
tg = tg ( 1 – 2) =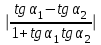
= 
.
Исследование прямой в пространстве ученые (Колодко Л.С.14, Логинов А.С.15 ) начинают следующими вопросами:
= 
=
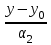, Тогда условия параллельности и перпендикулярности этих прямых описываются следующим образом:
L1 L2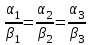 
; L1 L2 
.
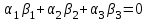Угол между прямыми L1 и L2 вычисляется по формуле
cos =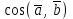 
= 
= 
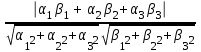, так как угол между направляющими векторам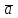и 
и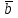 
данных прямых равен либо углу , либо смежному с ним углу – .
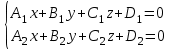
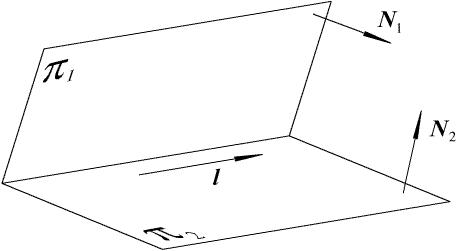
Рис. 1.4. Прямая как пересечение двух плоскостей
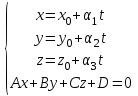
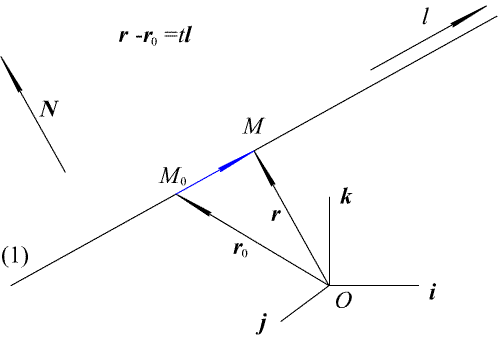
Рис. 1.5. Параметрическое уравнение прямой
Пучок прямых рассматривают Логинов А.С.16. Между множеством всех прямых пучка и множеством разбиения единицы
имеется взаимно однозначное соответствие, а именно: любая прямая из пучка
с
имеет свои барицентрические координаты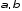
, с помощью которых записывается ее уравнение:
.
Многие исследователи (Финогенов А.А., Финогенова О.Б.17) предлагают подробные решения задач по разделу аналитической геометрии – прямая на плоскости, прямая в пространстве. А также включают набор формул и сведений, требуемый для решения предлагаемых задач.
Многолетнее преподавание курсов аналитической геометрии других ученых (Алания Л.А., Гусейн-Заде С.М., Дынников И.А. и др.18) убедило их в необходимости создание сборника задач. Все теоретические задачи в сборнике сопровождаются упражнениями различной степени сложности, чтобы студент с их помощью незамедлительно мог проверить, усвоил ли он новые алгоритмы и определения.
Сборник содержит огромное количество задач, расширенные теоретические сведения, в ответах к ряду задач даны краткие указания.
С.К. Соболев и В. Я. Томашпольский19 в своей работе излагают основы аналитической геометрии прямых на плоскости и в пространстве: различные виды уравнений прямых, исследование их взаимного расположения, приложения к планиметрии и стереометрии. В дополнение разбирают огромное количество примеров разной степени трудности. Включают задачи для самостоятельного решения, которые сопровождаются ответами и указаниями.
Бортаковский А.С.20 приводит основные понятия, теоремы и методы решения задач по всем уравнениям прямой. Описывает некоторые приложения аналитической геометрии в механике, теории оптимизации и математическом анализе.
Среди иностранных ученых следует отметить Д. Хилберта21. В качестве основы для анализа нашей интуиции пространства, профессор Гильберт начинает свое обсуждение с рассмотрения системы точек, прямых и плоскостей и выводит систему аксиом, объединяющих эти элементы в своих взаимоотношениях. Цель его исследований - обсуждение систематических отношений этих аксиом друг с другом, а также их связь друг с другом в отношении логического развития евклидовой геометрии.
Раздел 2. Методология решения задач
При решении задач, прежде всего, обращают внимание на известные величины и в зависимости от них составляют уравнение прямой. Или, наоборот, по известному уравнению анализируют геометрические свойства прямой.
Дано: уравнение прямой в параметрическом виде: r = r0 +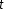
l и точка
r1=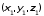
.
Первый способ.
(r
– r1 , l )=0 .
(r0 +
l – r1 , l )=0,
( l , l )= (r1 – r0 , l )
= (r1 – r0 , l ) / ( l , l ) . Радиус вектор искомой точки 
будет равен:
r2 = r0 + l (r1 – r0 , l ) / ( l , l ) .
Находим расстояние между двумя точками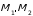
(рис. 2.1).
Рис. 2.1. Пересечение прямой и плоскости
Второй способ.
Строим параллелограмм на векторах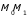
и l . Находим его площадь, как модуль векторного произведения и делим на длину основания 
l (рис. 2.2).
Рис. 2.2. Перпендикуляр на прямую
Если прямая задана в виде:
то ее пересечение с плоскостью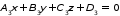
сводится к решению системы трех уравнений с тремя неизвестными (рис. 2.3)
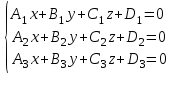
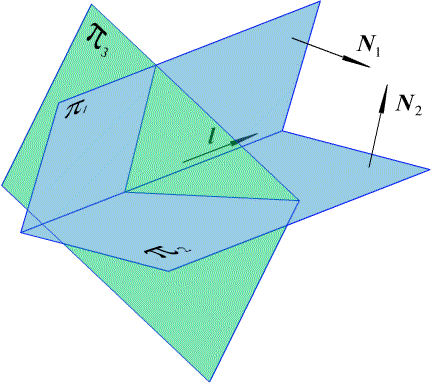
Рис. 2.3. Точка пересечения трех плоскостей
Проекция точки
на прямую (r – r0 , N )=0 на плоскости.
Если прямая задана общим уравнением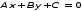
, N =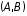 
, то составляется уравнение прямой r = r1 + N, проходящей через точку и направляющим вектором l = N . После чего находится точка пересечения этой прямой с исходной прямой:
(r1 + N – r0 , N )=0 
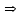
(N , N )= (r0 – r1 , N ) . Радиус вектор этой точки будет равен: r = r1 + N (r0 – r1 , N ) / (N , N ) (рис. 2.4) .
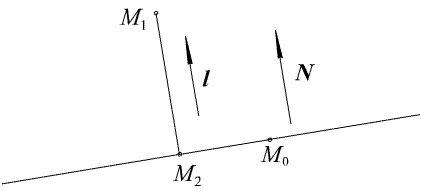
Рис. 2.4. Проекция точки на прямую
Аналогично решается задача нахождения проекции точки
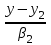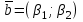, — направляющий вектор,авторы отмечают, что угол между направляющими векторами равен углу или смежному с ним тупому углу , поскольку эти векторы направлены параллельно прямым. Так как
cos () = cos , то cos =cos () . Поэтому
cos =
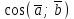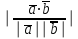= = .В случае, если прямые L1 и L2 заданы своими общими уравнениями:
L1: A 1 x + B 1 y + C 1 = 0,
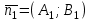— вектор нормали,L2: A 2 x + B 2 y + C 2 = 0,
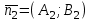, — вектор нормали,угол между векторами нормалей равен углу или смежному с ним тупому углу , поскольку эти векторы направлены перпендикулярно прямым. Тогда
cos = cos () =
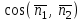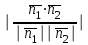= = .В случае, если прямые L1 и L2 заданы уравнениями
y = k 1 x + b1 и y = k2 x + b2
с углами 1 и 2 между прямыми L1 и L2 и осью ОХ, то
угол между L1 и L2 равен 1 – 2 или 2 – 1. Поэтому
tg = tg ( 1 – 2) =
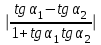= .Исследование прямой в пространстве ученые (Колодко Л.С.14, Логинов А.С.15 ) начинают следующими вопросами:
-
канонические уравнения прямой
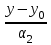= = , Тогда условия параллельности и перпендикулярности этих прямых описываются следующим образом:
L1 L2
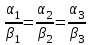; L1 L2 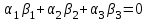.Угол между прямыми L1 и L2 вычисляется по формуле
cos =
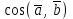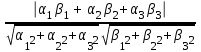= = , так как угол между направляющими векторам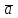и и 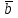данных прямых равен либо углу , либо смежному с ним углу – .-
2) Уравнение прямой в пространстве как пересечение двух плоскостей (рис. 1.4.)
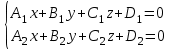
Рис. 1.4. Прямая как пересечение двух плоскостей
-
Параметрическое уравнение прямой в пространстве (рис. 1.5.)
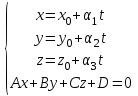
Рис. 1.5. Параметрическое уравнение прямой
Пучок прямых рассматривают Логинов А.С.16. Между множеством всех прямых пучка и множеством разбиения единицы
имеется взаимно однозначное соответствие, а именно: любая прямая из пучка с
имеет свои барицентрические координаты
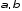, с помощью которых записывается ее уравнение: .Многие исследователи (Финогенов А.А., Финогенова О.Б.17) предлагают подробные решения задач по разделу аналитической геометрии – прямая на плоскости, прямая в пространстве. А также включают набор формул и сведений, требуемый для решения предлагаемых задач.
Многолетнее преподавание курсов аналитической геометрии других ученых (Алания Л.А., Гусейн-Заде С.М., Дынников И.А. и др.18) убедило их в необходимости создание сборника задач. Все теоретические задачи в сборнике сопровождаются упражнениями различной степени сложности, чтобы студент с их помощью незамедлительно мог проверить, усвоил ли он новые алгоритмы и определения.
Сборник содержит огромное количество задач, расширенные теоретические сведения, в ответах к ряду задач даны краткие указания.
С.К. Соболев и В. Я. Томашпольский19 в своей работе излагают основы аналитической геометрии прямых на плоскости и в пространстве: различные виды уравнений прямых, исследование их взаимного расположения, приложения к планиметрии и стереометрии. В дополнение разбирают огромное количество примеров разной степени трудности. Включают задачи для самостоятельного решения, которые сопровождаются ответами и указаниями.
Бортаковский А.С.20 приводит основные понятия, теоремы и методы решения задач по всем уравнениям прямой. Описывает некоторые приложения аналитической геометрии в механике, теории оптимизации и математическом анализе.
Среди иностранных ученых следует отметить Д. Хилберта21. В качестве основы для анализа нашей интуиции пространства, профессор Гильберт начинает свое обсуждение с рассмотрения системы точек, прямых и плоскостей и выводит систему аксиом, объединяющих эти элементы в своих взаимоотношениях. Цель его исследований - обсуждение систематических отношений этих аксиом друг с другом, а также их связь друг с другом в отношении логического развития евклидовой геометрии.
Раздел 2. Методология решения задач
При решении задач, прежде всего, обращают внимание на известные величины и в зависимости от них составляют уравнение прямой. Или, наоборот, по известному уравнению анализируют геометрические свойства прямой.
-
Расстояние от точки до прямой в пространстве
Дано: уравнение прямой в параметрическом виде: r = r0 +
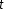l и точка r1=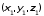 .Первый способ.
-
Составляем уравнение плоскости, проходящей через точку
, перпендикулярно прямой:
(r
– r1 , l )=0 .
-
Находим точку пересечения прямой и построенной плоскости:
(r0 +
l – r1 , l )=0, ( l , l )= (r1 – r0 , l ) = (r1 – r0 , l ) / ( l , l ) . Радиус вектор искомой точки будет равен: r2 = r0 + l (r1 – r0 , l ) / ( l , l ) .
Находим расстояние между двумя точками
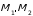(рис. 2.1). Рис. 2.1. Пересечение прямой и плоскости
Второй способ.
Строим параллелограмм на векторах
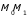и l . Находим его площадь, как модуль векторного произведения и делим на длину основания l (рис. 2.2). Рис. 2.2. Перпендикуляр на прямую
-
Определение координат точки пересечения прямой и плоскости в пространстве
Если прямая задана в виде:
то ее пересечение с плоскостью
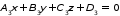сводится к решению системы трех уравнений с тремя неизвестными (рис. 2.3)
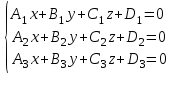
Рис. 2.3. Точка пересечения трех плоскостей
-
Определение координат проекции точки на прямую на плоскости, проекции точки на плоскость в пространстве
Проекция точки
на прямую (r – r0 , N )=0 на плоскости.Если прямая задана общим уравнением
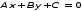, N = 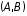, то составляется уравнение прямой r = r1 + N, проходящей через точку и направляющим вектором l = N . После чего находится точка пересечения этой прямой с исходной прямой: (r1 +
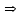
N – r0 , N )=0 (N , N )= (r0 – r1 , N ) . Радиус вектор этой точки будет равен: r = r1 + N (r0 – r1 , N ) / (N , N ) (рис. 2.4) . Рис. 2.4. Проекция точки на прямую
Аналогично решается задача нахождения проекции точки