Добавлен: 11.04.2024
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
на плоскость (r – r0 , N )=0 в пространстве. В векторном виде решение выглядит точно так же, как и в плоском случае.
Уравнение проектирующей прямой: r = r1 +
N , радиус вектор-проекции будет равен: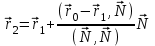 
(рис. 2.5)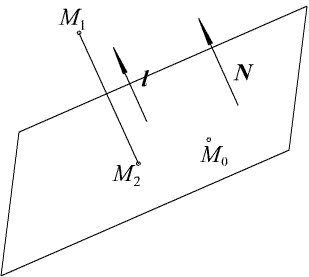
Рис. 2.5. Проекция точки на плоскость
Раздел 3. Практика применения прямой на плоскости и в пространстве в экономике
1.Практика применения уравнения прямой в экономике связано с исследованием взаимосвязей социально-экономических явлений.
По аналитическому выражению выделяют линейную связь, которая представляет собой статистическую связь между явлениями приближенно выраженную уравнением прямой линии. По направлению классифицируют:
- прямую связь - с увеличением или уменьшением значений факторного признака происходитувеличение или уменьшение значений результативного;
- обратную связь - значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного признака.
При исследовании взаимосвязей социально-экономических явлений применяется корреляционно-регрессионный анализ, метод, подразумевающий определение формы связи и измерение тесноты связи.
Определение формы связи подразумевает:
-
Нахождение уравнения регрессии -
Априорный теоретический анализ (с ростом факторного признака равномерно растет и результативный) -
Проверка априорного теоретического анализа с помощью графического анализа, т.е. наглядное представление о наличии и направлении (прямая/обратная) взаимосвязей между признаками.
При прямолинейном уравнении регрессии величина явления изменяется приблизительно равномерно в соответствии с изменением величины влияющего фактора.
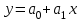
Коэффициент регрессии а1 показывает, на сколько в среднем отклоняется величина результативного признака Y при отклонении факторного признака X на одну единицу. При:
К примеру, между стоимостью основного капитала и выпуском продукции существует прямолинейная связь, выраженная уравнением прямой. Необходимо найти параметры а0 и а1.
Эта задача решается методом наименьших квадратов при помощи системы нормальных уравнений. Все расчеты ведутся по данным выборочного наблюдения.
Нахождение параметров позволит определить теоретические значения Y для разных значений xi. Причем а0 и а1 должны быть такими, , чтобы было достигнуто максимальное приближение к первоначальным значениям y теоретических значений Y.
2.Линейная модель издержек. Точка безубыточности.
При производстве x единиц любой продукции совокупные издержки(затраты) C(x) состоят из двух слагаемых ̶ постоянных (фиксированных)издержек F и переменных издержек V : C = F +V .
Постоянные издержки F− это издержки, не зависящие от числа единиц произведенной продукции. Они включают в себя амортизацию, аренду помещения, проценты по займам и т.п.
Переменные издержки V – это издержки, напрямую зависящие от количества произведенной продукции. Они включают в себя стоимость сырья, рабочей силы и т.п.
В простейшем случае переменные издержки прямо пропорциональны x − количеству произведенной продукции. Коэффициент пропорциональности a – это переменные затраты по производству одной единицы продукции (V = = a x).
Если обозначить через b фиксированные затраты, то получится уравнение, которое называют линейной моделью издержек:
C(x) = b + ax.
Совокупный доход, или выручка, R(x), получаемый предприятием от продажи x единиц продукции, определяется формулой
R(x) = px,
где p ─ цена единицы товара.
Если произведено и продано x единиц продукции, то прибыль P(x)
определяется формулой
P(x) = R(x) - C(x).
Точка, в которой прибыль обращается в нуль, называется точкой безубыточности.
Пример. Известно, что фиксированные издержки производства составляют 10 тыс. руб. в месяц, переменные издержки ̶ 30 руб. за единицу продукции, выручка ̶ 50 руб. за единицу продукции. Требуется составить функцию прибыли и построить ее график.
Решение. По условию задачи фиксированные или постоянные издержки F =10000. Так как переменные издержки по производству одной единицы продукции по условию задачи равны 30 руб. (a = 30), то переменные издержки, зависящие от количества произведенной продукции,
V = 30 x, где x ̶ количество произведенной продукции. Таким образом, совокупные издержки составляют C(x) 10000 30x. Совокупный доход, получаемый от продажи x единиц продукции, определяется следующим образом R(x) 50 x.
Построим графики функций дохода и издержек (рис 3.1.).
Рис. 3.1. Графики функций дохода и издержек
Точку пересечения прямых C(x) 10000 30x и R(x) 50 x найдем следующим образом: C(x) R(x), тогда 1000030x 50x, следовательно, x 500, C(x) R(x) 25000.
Прибыль, получаемую предприятием, можно найти по формуле P(x) R(x) C(x) 50 x (10000 30 x) 20 x 10000, P(x) 20 x 10000.
Построим график функции прибыли. При x 500 P(x) 0. Следовательно, координаты первой точки (500;0). При x 600 P(x) 2000; получили вторую точку (600; 2000). Через две точки на плоскости проведем прямую, которая является графиком функции P(x) (рис. 3.2.).
Рис. 3.2. График функции P(x)
Как видно из графика, при малых значениях x прибыль отрицательна (график P(x) расположен ниже оси Ox), т.е. производство убыточно. При увеличении x прибыль возрастает, в точке с абсциссой x 500 она обращается в нуль (точка безубыточности) и после этого становится положительно.
3. Законы спроса и предложения. Количество товара, которое покупатели приобретут на рынке, зависит от цены на этот товар. Соотношение между ценой и количеством купленного товара называется функцией или законом спроса.
Количество товара, которое производители выставят на продажу, также зависит от цены на этот товар. Соотношение между ценой и количеством товара, выставленного на продажу, называется функцией или законом предложения.
В простейшем случае эти функции являются линейными (рис. 3.3.).
Рис. 3.3. Законы спроса и предложения
Закон спроса обозначен через D, закон предложения через S; x ̶ количество товара, p - цена на этот товар.
Уравнение спроса можно составить, если заданы две точки, лежащие на его графике. Для этого нужно использовать уравнение прямой, проходящей через две заданные точки:
Точка пересечения кривых спроса и предложения (х0; р0) называется точкой рыночного равновесия. Соответственно, р0 называется равновесной ценой, а х0 - равновесным количеством (равновесным объемом продаж).
Если известен закон спроса p(x), то совокупный доход R можно выразить через x : R x p .
Очень часто правительство вводит налог t на товар или предоставляет субсидию s, чтобы население могло приобрести товар по разумной цене.
При использовании линейных моделей предполагается, что спрос определяется только ценой товара на рынке рс, а предложение - только ценой ps, получаемой поставщиками. Эти цены связаны между собой следующими уравнениями:
где t и s - соответственно налог и субсидия на единицу товара.
Таким образом, при введении налога или субсидии уравнение спроса D не изменится. График функции предложения поднимется на t единиц вверх (линия S) или опустится на s единиц вниз (линия S) (рис. 3.3.).
Некоторые налоги, например НДС (налог на добавленную стоимость), пропорциональны цене. В этом случае точка пересечения графика предложения S с осью Ox остается той же, но меняется угол наклона графика к оси Ox.
Пример. Законы спроса и предложения на некоторый товар определяются уравнениями
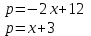
а) Найти точку рыночного равновесия.
б) Найти точку равновесия после введения налога, равного 3 на единицу продукции. Найти увеличение цены и уменьшения равновесного объема
продаж. Найти доход государства после введения этого налога.
в) Какая субсидия приведет к увеличению объема продаж на 2 единицы?
г) Вводится пропорциональный налог, равный 20%. Найти новую точку равновесия и доход правительства.
Решение. а) В точке рыночного равновесия спрос равен предложению. Поэтому найдем точку равновесия из соотношения: -2x +12 = x +3, x = 3. При этом p 6. Точка M (3, 6) является точкой рыночного равновесия (рис. 3.4.).
Рис. 3.4. Рыночное равновесие
б) По условию задачи введенный налог t 3. Найдем новую точку рыночного равновесия. После введения налога уравнение спроса не изменяется, т.е.
D: pс2x 12. Составим систему для определения точки равновесия. Для этого используем соотношение между ценой на рынке pс и ценой ps, получаемой поставщиками: следовательно,
pсx 6, т.к. psx 3. Система будет иметь вид:
Решая эту систему, получаем новую точку равновесия M(2; 8). Следовательно, после введения налога равновесный объем уменьшился на 1 единицу, а равновесная цена увеличилась на 2 единицы. Доход государства после введения налога будет равен 23 6.
в) Пусть введена субсидия. В этом случае уравнение спроса D не изменяется, т.е. D: pс2x 12. Используем соотношение между ценой на рынке pси ценой ps, получаемой поставщиками, где psx 3.
Запишем систему для определения точки рыночного равновесия:
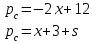
Если объем продаж увеличится на 2 единицы, то он составит x 32, x 5.
Подставляя x 5 в указанную выше систему уравнений, получим
2x 12 x 3s, 2512 53s, s 6 - величина субсидии, приводящая к увеличению объема продаж на 2 единицы.
Заключение
В данной работе были изучены методы исследования прямой на плоскости и в пространстве, а также практики их применения.
На основе изложенного материала были рассмотрены базовые задачи по следующим темам:
1.Расстояние от точки до прямой в пространстве
2.Определение координат точки пересечения прямой и плоскости в пространстве
3.Определение координат проекции точки на прямую на плоскости, проекции точки на плоскость в пространстве
Так как необходимость изучения прямой на плоскости и в пространстве связана с широким использованием математических методов в современной экономической практике, были предложены и решены конкретные задачи по следующим темам:
- исследование взаимосвязей социально-экономических явлений;
- линейная модель издержек. Точка безубыточности;
- законы спроса и предложения.
Таким образом, цели и задачи, поставленные в данной работе