Сумма частот всех разрядов, очевидно, должна быть равна единице.

Построим таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты. Эта таблица называется статистическим рядом:

Ii	X1; X2	X2; X3		Xi; Xi+1		Xk; Xk+1
P *i	P *1	P *2		P *i		P *k

Здесь Ii, — обозначение i-го разряда; x[t xi+l— его границы; p*t — соответствующая частота; k — число разрядов.

Пример 1. Произведено 500 измерений боковой ошибки наводки при 'стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд:

Ii	— 4;-3	-3;-2	-2; -1	-1;0	0; 1	1;2	2;3	3;4
mi	6	25	72	133	120	88	46	10
P* i	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020

' Здесь Ii обозначены интервалы значений ошибки наводки mi; — число наб­людений в данном интервале,
P* i = mi/n - соответствующие частоты.

При группировке наблюденных значений случайной величины по разрядам возникает вопрос о том, к какому разряду отнести значе­ние, находящееся в точности на Границе двух разрядов. В этих Случаях можно рекомендовать (чисто условно) считать данное зна-; чение принадлежащим в равной мере к обоим разрядам и "прибав­лять к числам mt того и другого разряда по 1/2.

Число разрядов, на которые следует группировать статистический j 'Материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика пока­зывает, что в большинстве случаев рационально выбирать число разрядов порядка 10 — 20. Чем богаче и однороднее статистический Материал, тем большее число разрядов можно выбирать при состав­лении статистического ряда. Длины разрядов могут быть как одина­ковыми, так и различными. Проще, разумеется, брать их одинаковы­ми. Однако при оформлении данных о случайных величинах, рас­пределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие, чем в области малой плотности.

---

Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим обра­зом. По оси абсцисс откладываются разряды, и на каждом из раз­рядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине

разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.

В качестве примера можно привести гистограмму для ошибки наводки, построенную по данным статистического ряда, рассмотрен­ного в примере 1 (рис. 7.3.1).

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь,



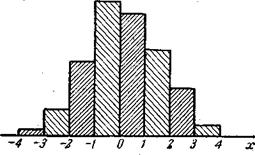
равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины X.

Пользуясь данными статистического ряда, можно приближенно построить и статистическую функцию распределения величины X, Построение точной статистической функции распределения с несколь­кими сотнями скачков во всех наблюденных значениях X слишком трудоемко и себя не оправдывает. Для практики обычно достаточно построить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобно взять границы X1, X2, ... разрядов, которые фигурируют в статистическом ряде. Тогда, очевидно,

F*(x1)=0

F*(x2) = 
F*(x3) = Pi + Pi

• • • • (7.3.2)

Соединяя полученные точки ломаной линией или плавной кривой, получим приближенный график статистической функции распреде-

---

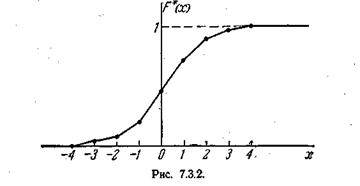
Пример 2. Построить приближенно статистическую функцию распре­деления ошибки наводки по данным статистического ряда примера 1.

Решение. Применяя формулы (7.3.2), имеем:

F*(-4) = 0; F* (- 3) = 0,012; F* (-2) = 0,01 2 + 0,050 = 0,062;

F*(-l) = 0,206; F* (0) = 0,472; F*(l)= 0,712; F* (2) = 0,888;

F*(3) = 0,980; F* (4) = 1,000.

Приближенный график статистической функции распределения дан на рис.7.3.2.

ГЛАВА 3 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ

В главе 5 мы ввели в рассмотрение различные числовые характеристики случайных величин: математическое ожидание, дисперсию, начальные и центральные моменты различных порядков. Эти число­вые характеристики играют большую роль в теории вероятностей. Аналогичные числовые характеристики существуют и для статисти­ческих распределений. Каждой числовой характеристике случайной величины X соответствует ее статистическая аналогия. Для основной характеристики положения — математического ожидания случайной величины — такой аналогией является среднее арифметическое наблю­денных значений случайной величины:

М*[Х] = (7.4,1)

где xt — значение случайной величины, наблюденное в 1-й опыте п — число опытов.

Эту характеристику мы будем в дальнейшем называть стати­стическим средним случайной величины.

Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается, (сходится по ве­роятности) к математическому ожиданию. При достаточно большом п статистическое среднее может быть принято приближенно равным математическому ожиданию. При ограниченном числе опытов стати­стическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех число­вых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие чис­ловые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она пред­ставляет собой математическое ожидание случайной величины

.Х2 = (Х — mх)2:

D[X] = M[X*] = M[(X — mx)2}. (7.4.2)

Если в этом выражении заменить математическое ожидание его статистической аналогией — средним арифметическим, мы получим статистическую дисперсию случайной величины X:

---

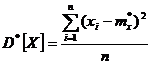 (7.4.3)

где т*х — М*[Х] — статистическое среднее.

Аналогично определяются статистические начальные и централь­ные моменты любых порядков:

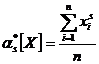 (7.4.4)

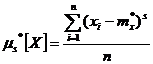 (7.4.5)

Все эти определения полностью аналогичны данным в главе 5 определениям числовых 'характеристик случайной величины, с той разницей, что в них везде вместо математического ожидания фигу­рирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном n могут быть приняты приближенно равными им.

Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были выведены в главе 5 для математических моментов. В частности, статистический первый. центральный момент всегда равен нулю:

= - m*x = m*x - m*x = 0

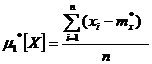Соотношения между центральными и начальными моментами также сохраняются:

= - 2m*x +(m*x)2=α*2 - (m*x)2

и т. д.

При очень большом количестве опытов вычисление характеристик,10 формулам (7.4.1) — (7.4.5) становится чрезмерно громоздким, и можно применить следующий прием: воспользоваться теми же ^разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде Постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характе­ристики будут выражаться приближенными формулами:

---

m*x = M*[X] =  , (7.4.7)

D*x = D* [X] = , (7.4.8)

 =   (7.4.9)

 (7.4.10)

где xt — «представитель» 1-го разряда, р* — частота 1-го разряда, k — число разрядов.

Как видно, формулы (7.4.7) — (7.4.10) полностью аналогичны формулам п°п° 5.6 и 5.7, определяющим математическое ожидание, дисперсию, начальные и центральные моменты прерывной случайной

величины X, с той только разницей, что вместо вероятностей р{ в них стоят частоты р*, вместо математического ожидания тх — ста­тистическое среднее тх*, вместо числа возможных значений случайной величины — число разрядов.

ЗАКЛЮЧЕНИЕ

В ходе проделанной работы мной были изучены построение распределений и оценка выборочных характеристик случайных величин на основе опытных данных. Также я ознакомилась с разделами высшей математики: «Основные задачи математической статистики», «Статистический ряд», «Гистограмма». И изучила числовые характеристики статистического распределения и выравнивание статистических рядов

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1) Гмурман В.Е Теория вероятностей и математическая статистика

2) Гмурман В.Е Руководство к решению задач по теории вероятностей и математической статистике

3) Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах

4) Пискунов Н.С. Дифференциальное и интегральное исчисления. Т 2

генеральный совокупность статистический распределение.

---

Смотрите также файлы

• Семей аласыны Дйсенбі алматаев атындаы мемлекеттік жоары медицина колледжі шж кмк 5 Дріс Таырып.docx

• Виды административных наказаний.docx

• См. Бытие, выступающее в системе философии одним из базисных её компонентов. Как раздел.docx

• Доклад На тему нормы права.docx

• Жпалы аурулар іліміне кіріспе.docx