Файл: Контрольная работа По дисциплине Теория электрических цепей Новосибирск, 2023 г Оглавление Задача 1 3.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.17)
2.2. Использование интеграла наложения.
В отличие от интеграла Дюамеля в интеграле наложения не учитываются дополнительными слагаемыми скачки входного напряжения:
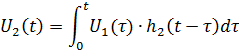
Для интервала времени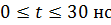
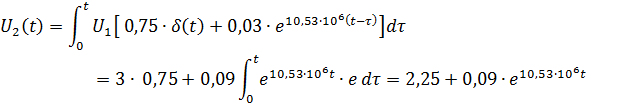
Для интервала времени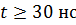
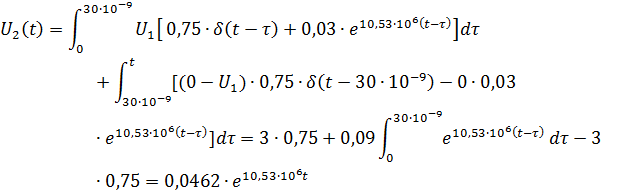
Сравнение результатов расчетов напряжения с использованием интегралов наложения и Дюамеля показывает, что они совпадают между собой.
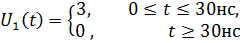
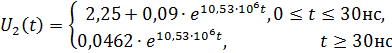
Диаграмма выходного напряжения строится с использованием формул (3.16) и (3.17) путем подстановки в них соответствующих моментов времени. Результаты расчетов сводятся в таблицу 5.
Таблица 5
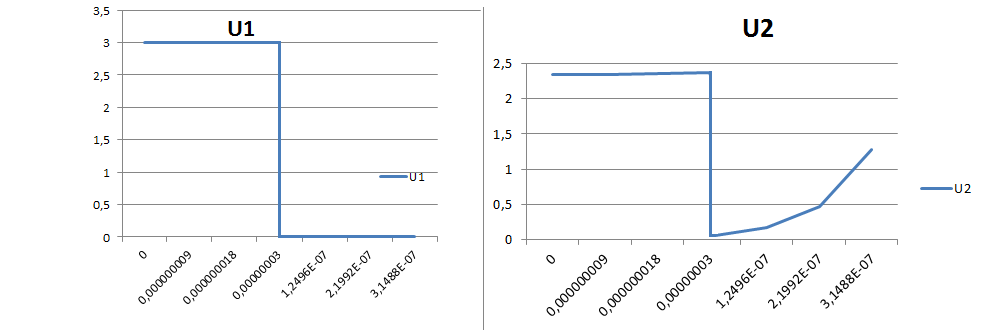
Рисунок 3.8. Временные диаграммы входного и выходного напряжений.
4. Расчет комплексной спектральной плотности входного и выходного сигналов.
Для расчета комплексной спектральной плотности непериодического сигнала f(t) произвольной формы используется прямое преобразование Фурье:
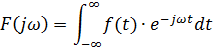
Комплексная спектральная плотность выходного сигнала находится по формуле:
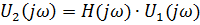
КПФ цепи находится как отношение комплексного значения гармонического напряжения на выходе цепи к комплексному значения гармонического напряжения той же частоты, приложенному ко входу цепи:
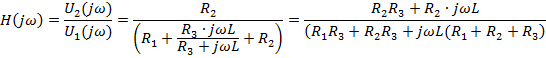
Комплексная спектральная плотность входного сигнала:
5. Расчет графиков модулей
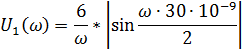
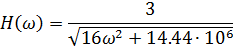
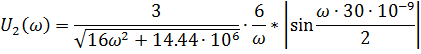
Для построения графиков полученных функций необходимо выбрать расчетные точки по частоте. Учтем, что спектральная плотность одиночного прямоугольного импульса измеряется в вольт × секундах [B × c] и что она обращается в ноль на частотах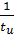
, 
, 
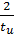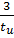и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна 
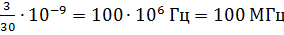. Результаты расчетов сводим в таблицу 3.
Таблица 3 - спектральная плотность сигнала
По данным таблицы 3 строим графики спектральных функций (рисунок 12).
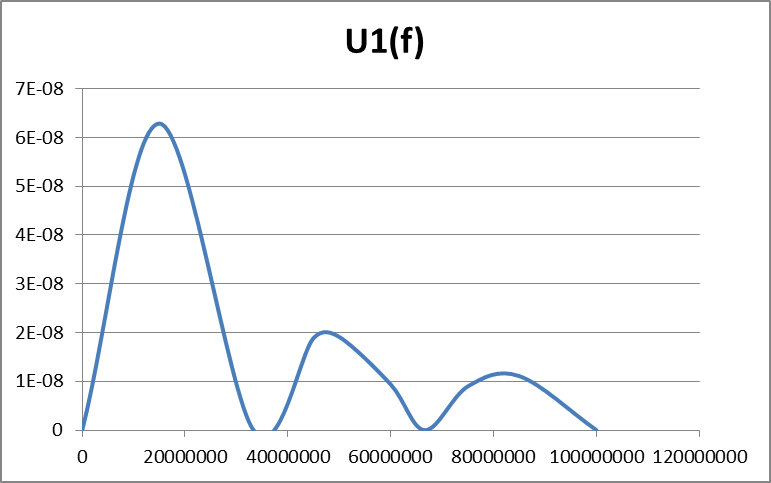
Рисунок 12а
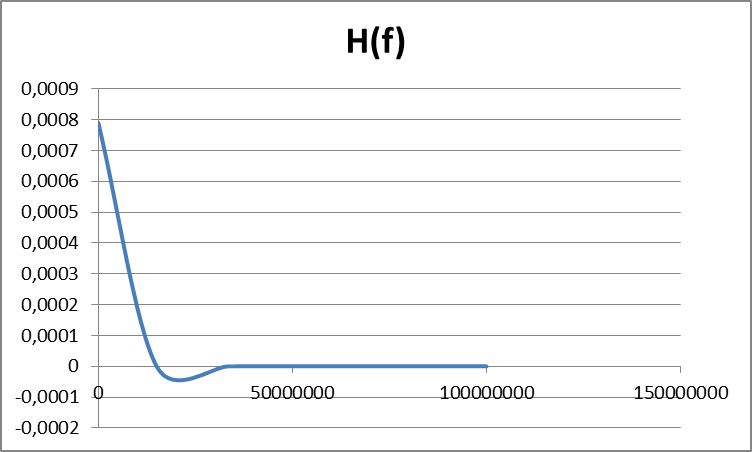
Рисунок 12а
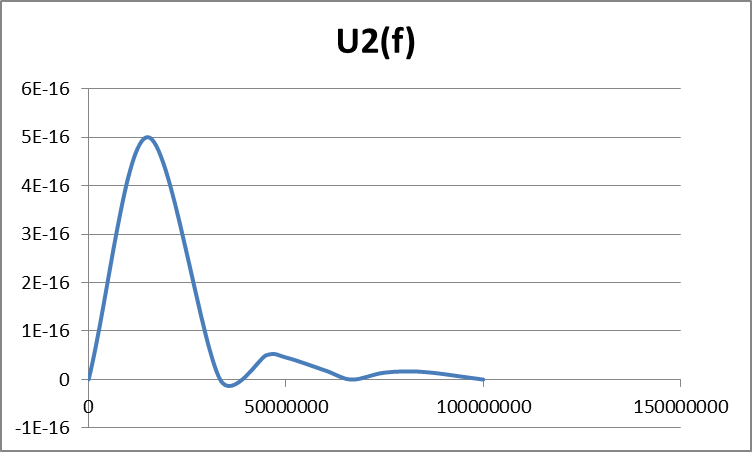
Рисунок 12в
2.2. Использование интеграла наложения.
В отличие от интеграла Дюамеля в интеграле наложения не учитываются дополнительными слагаемыми скачки входного напряжения:
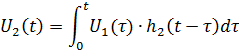
Для интервала времени
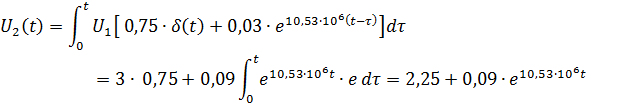
Для интервала времени
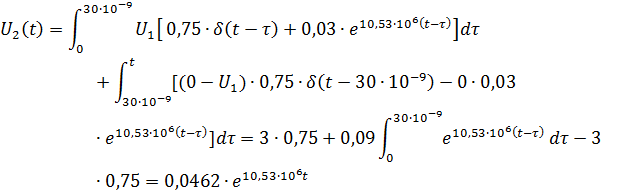
Сравнение результатов расчетов напряжения с использованием интегралов наложения и Дюамеля показывает, что они совпадают между собой.
-
Построение временной диаграммы входного и выходного напряжений.
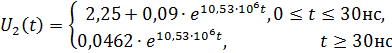
Диаграмма выходного напряжения строится с использованием формул (3.16) и (3.17) путем подстановки в них соответствующих моментов времени. Результаты расчетов сводятся в таблицу 5.
Таблица 5
| Время | 0 | 0,3  | 0,6 |  |  |  |  |  |
| нс | 0 | 9 | 18 | 30 | 30 | 124,96 | 219,92 | 314,88 |
 | 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 |
 | 2,34 | 2,35 | 2,36 | 2,37 | 0,06 | 0,17 | 0,47 | 1,27 |
Рисунок 3.8. Временные диаграммы входного и выходного напряжений.
4. Расчет комплексной спектральной плотности входного и выходного сигналов.
Для расчета комплексной спектральной плотности непериодического сигнала f(t) произвольной формы используется прямое преобразование Фурье:
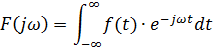
Комплексная спектральная плотность выходного сигнала находится по формуле:
КПФ цепи находится как отношение комплексного значения гармонического напряжения на выходе цепи к комплексному значения гармонического напряжения той же частоты, приложенному ко входу цепи:
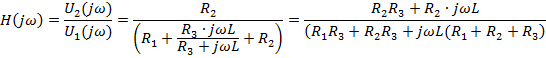
Комплексная спектральная плотность входного сигнала:
5. Расчет графиков модулей
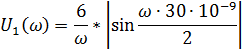
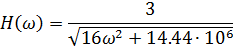
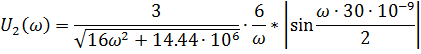
Для построения графиков полученных функций необходимо выбрать расчетные точки по частоте. Учтем, что спектральная плотность одиночного прямоугольного импульса измеряется в вольт × секундах [B × c] и что она обращается в ноль на частотах
, , и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна . Результаты расчетов сводим в таблицу 3.Таблица 3 - спектральная плотность сигнала
 |  |  |  |  |
| 0 | 0 | 0 | 0,000789 | 0 |
| 15 | 94.25*106 | 6,28782E-08 | 7,96E-09 | 5E-16 |
| 33.33 | 209.4*106 | 9E-16 | 3,58E-09 | 3,22E-24 |
| 45 | 282.7*106 | 1,89077E-08 | 2,65E-09 | 5,02E-17 |
| 66.67 | 418.9*106 | 1,90986E-08 | 2,39E-09 | 4,56E-17 |
| 75 | 471.2*106 | 9,35489E-09 | 1,99E-09 | 1,86E-17 |
| 100 | 628.3*106 | 4,5E-16 | 1,79E-09 | 8,06E-25 |
По данным таблицы 3 строим графики спектральных функций (рисунок 12).
Рисунок 12а
Рисунок 12а
Рисунок 12в