Файл: Контрольная работа По дисциплине Теория электрических цепей Новосибирск, 2023 г Оглавление Задача 1 3.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: «Теория электрических цепей»
Новосибирск, 2023 г
Оглавление
Задача 3.1 3
Задача 3.2 10
Задача 3.1
Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени
-
Перерисуйте схему цепи (см. рис. 3.1) для Вашего варианта (таблица 1).
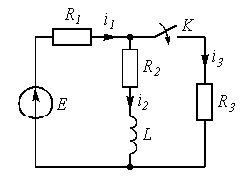
Рисунок 3.1. Схема цепи.
-
Выпишите числовые данные для Вашего варианта (таблица 2).
3. Рассчитайте все токи и напряжение на
4. Рассчитайте классическим методом переходный процесс в виде
в схемах 1 – 5,
5. Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%.
6. Рассчитайте ток
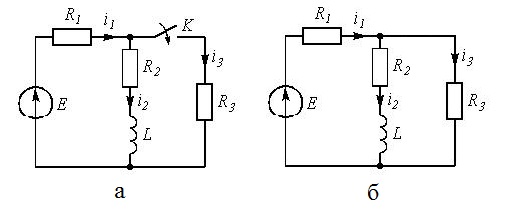
Рисунок 3.2
Решение:
1. Находим токи и напряжение на
1.1 Момент
Так как при последовательном соединении резисторов сила тока во всей цепи будет одинакова, то:
1.2. Момент
Остальные величины находим путем составления и решения системы уравнений по законам Кирхгофа, описывающих электрическое состояние цепи в момент
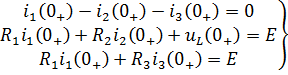
После числовых подстановок с учетом (3.1) получим:
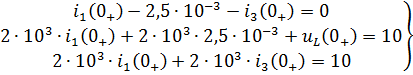
Решая систему, находим:
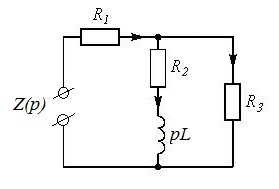
Рисунок 3.3
1.3. Момент
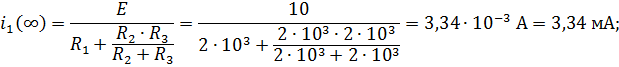
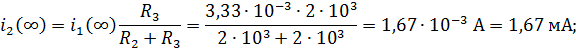
2. Расчет токов
Переходный процесс в цепях первого порядка (с одним реактивным элементом) описывается уравнением вида
где
2.1. Характеристическое уравнение для расчета
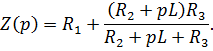
Принимая
Решение уравнения дает корень
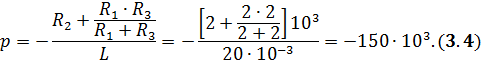
Величина
называется постоянной времени цепи.
2.2. Расчет
В соответствии с (3.3) запишем:
Учтем, что
Откуда
. Тогда
2.3. Расчет
Воспользуемся законом Ома для индуктивности
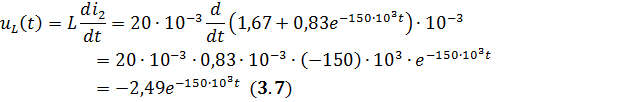
2.4. Расчет
2.5. Проверка правильности расчетов производится путем анализа выражений (3.6), (3.7) и (3.8) в моменты времени
Полученные значения всех величин совпадают с результатами расчетов в п. 1.
3. Построение графиков переходного процесса.
Для построения графиков необходимо составить таблицу значений
Таблица 3
| | | | | | | | |
| | 0,0 | 3,4 | 6,7 | 10,1 | 13,4 | 20,1 | 26,8 |
| | 2,5 | 2,2 | 2,0 | 1,9 | 1,8 | 1,7 | 1,7 |
| | 1,3 | 1,4 | 1,5 | 1,6 | 1,6 | 1,6 | 1,7 |
| | -2,5 | -1,5 | -0,9 | -0,6 | -0,3 | -0,1 | 0,0 |

