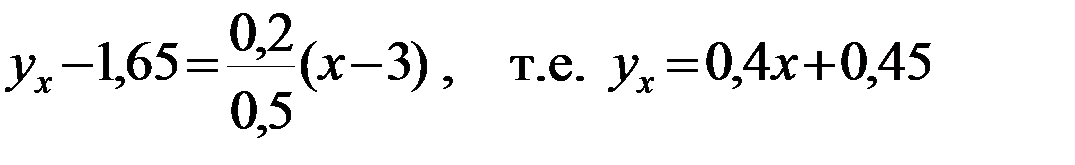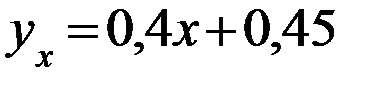Файл: Задача 1 в результате некоторого тестирования 20 испытуемых была получена следующая выборка 5, 7, 9, 4, 7, 5, 4, 4, 9, 7, 5, 4, 5, 4, 5, 5, Ранжировать ряд..docx
Добавлен: 24.04.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Это граничная точкаРанговый коэффициент корреляции Спирмена:
Статистика
Гипотезу Н0 отвергаем и принимаем гипотезу Н1 на уровне значимости 5%. Между результатами исследований существует некая связь.
Задача 5
Даны измерения двух случайных величин:
| X | 1 | 4 | 9 | 16 | 25 |
| Y | 23,9 | 14,9 | 8,1 | 3 | 0,1 |
Задание:
1 Построить корреляционное поле XY. 2 Вычислить коэффициент корреляции между X и Y, сделать вывод. 3 Найти уравнение линейной регрессии и построить его на корреляционном поле. 4 Доказать (или опровергнуть) гипотезу о равенстве нулю генерального коэффициента корреляции.Решение:
1) Выборочный коэффициент корреляции:
= 
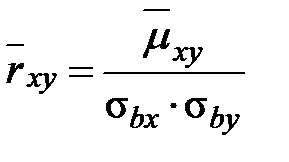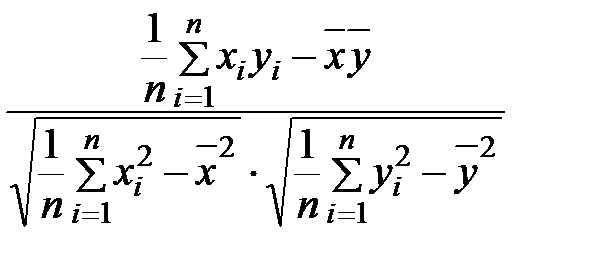;2) линейное уравнение регрессии Y на X :
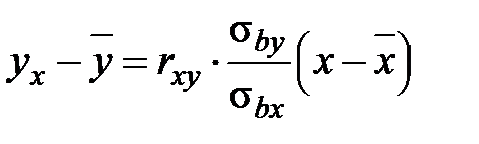,где
, 
, 
, 
.
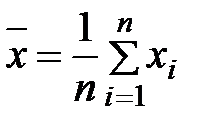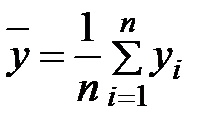
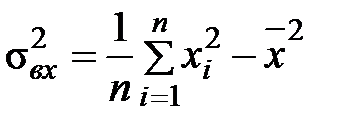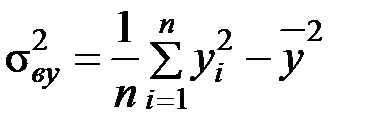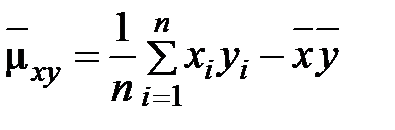
Проведем необходимые вычисления, для чего составим расчетную таблицу:
| № |  |  |  |  |  |
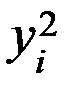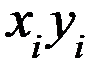| | | 1,25 | | 1,5625 | 2,5 |
| | 2,5 | 1,45 | 6,25 | 2,1025 | 3,625 |
| | | 1,65 | | 2,7225 | 4,95 |
| | 3,5 | 1,85 | 12,25 | 3,4225 | 6,475 |
| | | 2,05 | | 4,2025 | 8,2 |
| ∑ | | 8,25 | 47,5 | 14,0125 | 25,75 |
Тогда получаем:
,
,
,
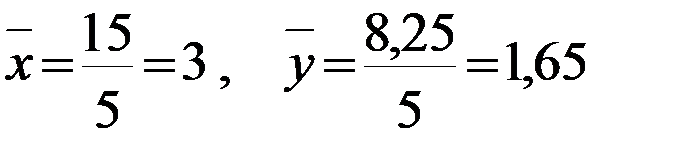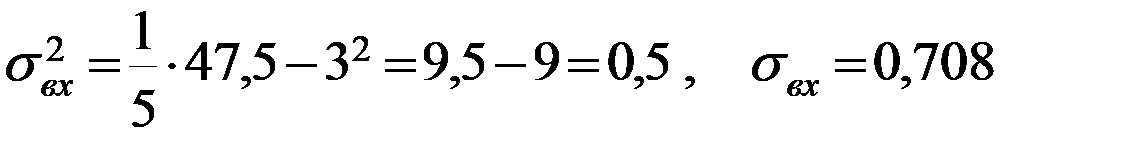
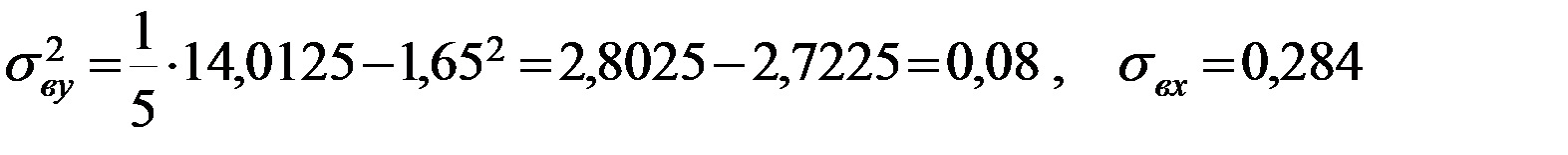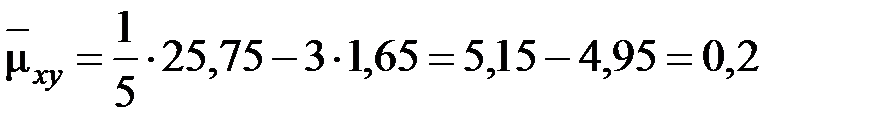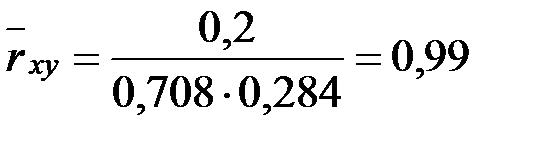.Запишем уравнение линейной регрессии Y на X :
, 
