Файл: Исследование процесса поступления сообщений на системы коммутации.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 31
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Построить кривые распределения Эрланга и Энгсета и получить численное доказательство того, что сумма вероятностей состояний полнодоступного пучка при обслуживании примитивного и простейшего потока вызовов составит
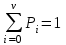
-
Установить взаимосвязь между рассматриваемыми моделями, выявив условия перехода формулы Энгсета в первую формулу Эрланга. -
По результатам проведенных исследований сформулировать выводы относительно соответствия процесса обслуживания реального потока сообщений математическим моделям, описываемым первой формулой Эрланга и формулой Энгсета.
Таблица 5 – Результаты измерений числа одновременно занятых линий
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 день | 1 | 3 | 1 | 4 | 5 | 3 | 2 | 0 | 1 | 3 | 1 | 1 |
| 2 день | 0 | 1 | 1 | 2 | 1 | 0 | 1 | 3 | 5 | 5 | 4 | 2 |
| 3 день | 2 | 2 | 5 | 5 | 5 | 5 | 4 | 2 | 1 | 1 | 0 | 0 |
Таблица 6 – Исходные данные
| с | t, c | ν | N |
| 90 | 100 | 5 | 20 |
Решение:
-
Интенсивность обслуженной нагрузки определяется как
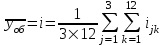 , где
, где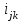 - число одновременно занятых линий при каждом измерении (k = 1,2,..,12) в j-й день измерений (j = 1,2,3).
- число одновременно занятых линий при каждом измерении (k = 1,2,..,12) в j-й день измерений (j = 1,2,3).Для 1 дня:
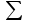 = 25
= 25Для 2 дня:
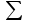 = 25
= 25Для 3 дня:
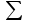 = 32
= 32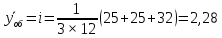
Интенсивность поступающей нагрузки:
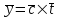
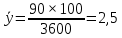
Интенсивность потерянной нагрузки:
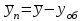
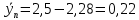
Вероятность потерь по нагрузке:
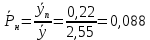
-
Предположим, что поступающий поток вызовов является простейшим потоком. Для его полного описания достаточно знать интенсивность потока μ, зная которую можно оценить все остальные характеристики потока (параметр λ, функцию распределения промежутков между вызовами А(х), вероятность поступления определенного числа вызовов k за некоторый промежуток времени t – Pk(t)).
Если принять за единицу времени ЧНН, то правомерно приравнять эмпирическое значение среднего числа вызовов в ЧНН его теоретическому значению:
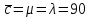 .
.Переходя к расчету характеристик модели обслуживания М/М/ν/К (процесс обслуживания простейшего потока вызовов полнодоступным пучком линий с потерями при показательном распределении длительности обслуживания), К=ν, также правомерно приравнять эмпирическое значение интенсивности поступающей нагрузки
 его теоретическому значению
его теоретическому значению
у:
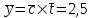
Модель М/М/ν/К, К=ν описывается первым распределением Эрланга:
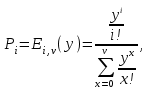
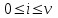
Р5 = 0,069731
Р4 = 0,139462
Р3 = 0,22314
Р2 = 0,267767
Р1 = 0,214214
Р0 = 0,085686
где
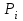 -вероятность того, что в полнодоступном пучке из ν линий, на который поступает нагрузка интенсивности у, занято точно i линий .
-вероятность того, что в полнодоступном пучке из ν линий, на который поступает нагрузка интенсивности у, занято точно i линий .Вероятность занятости в пучке всех ν линий Рν равна вероятности потерь по вызовам Рв, времени Рt и нагрузке Рн:
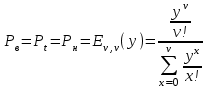
Согласно таблицам из Приложения 2 вероятность занятости в пучке всех ν линий Рν равна 0,0697, т.е. Рв=Рt=Рн=0,0697
Интенсивность обслуженной нагрузки равна:
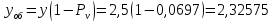
Интенсивность потерянной нагрузки:
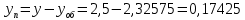
Определим отклонения теоретических значений Рн и уоб от эмпирических,
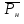 и
и 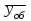 , в %:
, в %: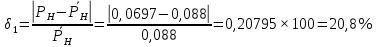
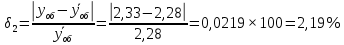
-
Предположим, что поступающий поток вызовов является примитивным, который характеризуется переменным параметром λi, пропорциональным числу свободных источников (абонентов):
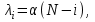
где N – общее число источников, i – число занятых источников, α – параметр потока одного свободного источника.
В сущности, примитивный поток – это суммарный поток, т.е. от каждого свободного источника поступают простейшие взаимно независимые потоки.
Модель обслуживания примитивного потока полнодоступным пучком (модель М/М/ν/K/N, К=ν) описывается формулой Энгсета.
Распределение Энгсета Pi и характеристики качества прохождения нагрузки имеют следующий вид:
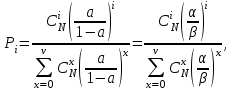

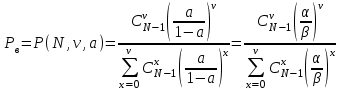
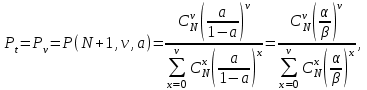
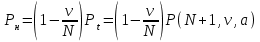 ,
,при этом Рн < Pв < Pt = Pν, где α/β= α×1/β – среднее число вызовов, посылаемое одним свободным источником в течение интервала времени, равного средней длительности обслуживания;
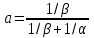 - нагрузка, создаваемая одним источником, т.е. отношение средней длительности обслуживания к сумме средней длительности обслуживания и расстояния от момента окончания обслуживания до момента посылки нового вызова.
- нагрузка, создаваемая одним источником, т.е. отношение средней длительности обслуживания к сумме средней длительности обслуживания и расстояния от момента окончания обслуживания до момента посылки нового вызова.Нагрузка, создаваемая одним источником равна:
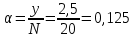
Тогда согласно Приложению 3:
Рв = 0,0564
Pt = Pν = 0,0665
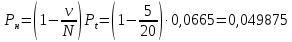
Распределение вероятностей Pi рассчитывается через рекуррентное соотношение, начиная с i=ν:
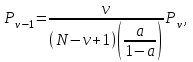
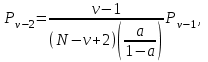
. . . . . . .
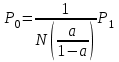
Р5 = 0,0564
Р4 = 0,1455
Р3 = 0,2396
Р2 = 0,2796
Р1 = 0,2068
Р0 = 0,0721
При расчете характеристик модели М/М/ν/К/N, К=ν будем исходить из численного равенства между эмпирическим значением интенсивности поступающей нагрузки
 и ее математическим ожиданием (
и ее математическим ожиданием (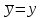 ).
).Интенсивность поступающей нагрузки на ν линий от N источников (по определению среднего значения)
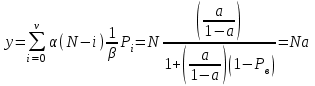
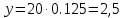
Интенсивность обслуженной нагрузки (среднее число занятых линий i):
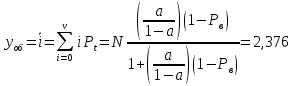
Интенсивность потерянной нагрузки:
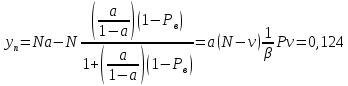
Определим отклонения теоретических значений Рн и уоб от эмпирических,
 и
и  , в %:
, в %: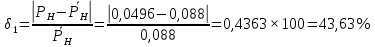
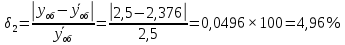
-
Сумма вероятностей состояний полнодоступного пучка при обслуживании примитивного и простейшего потоков составляет 1:

Это легко доказать.
Для простейшего потока:
0,069731+0,139462+0,22314+0,267767+0,214214+0,085686= 1
Для примитивного потока:
0,0564+0,1455+0,2396+0,2796+0,2068+0,0721=1
-
Характер зависимости величины поступающей нагрузки na от емкости пучка линий v, который обслуживает вызовы примитивного потока, поступающие от фиксированного числа источников n, такой же, как при обслуживании вызовов простейшего потока. Однако на пропускную способность пучка влияет число источников вызовов n: в области малых потерь с уменьшением n увеличивается пропускная способность пучка. При увеличении потерь Рв:
- существенно уменьшается влияние n на пропускную способность пучка;
- сокращается различие между пропускной способностью пучков, обслуживающих вызовы примитивного и простейшего потоков.
-
По результатам проведенных исследований можно Сопоставить реальный поток обслуживания вызовов и две математические модели: простейший поток и примитивный поток.
У простейшего потока интенсивность обслуженной нагрузки отличается от реальной на 2.19%, а у примитивного потока – на 4.96%.
Вероятность потерь по нагрузке отличается от реального потока на 20,8 %, у примитивного – на 43.63 %.

