Таким образом, приходим к выводу, что наш поток по своим характеристика ближе к простейшему потоку, эта модель описывает его более точно, чем примитивный поток.

Задание 3 Оценка пропускной способности управляющих устройств систем коммутации

Условие

Ступень группового искания (ГИ) координатной АТС с индивидуальными управляющими устройствами (маркерами) для каждого блока комплектуется из s коммутационных блоков. Средняя длительность занятия входа ступени ГИ равна t_вх. На ступень искания поступает поток вызовов, создающий нагрузку y_вх. Управляющие устройства работают по системе с ожиданием. Средняя длительность занятия одним вызовом управляющего устройства равна h, допустимое время – t_доп.

Необходимо

Оценить следующие характеристики процесса обслуживания.

1. Рассчитать качественные показатели работы управляющих устройств ступени ГИ при постоянной и показательно распределенной длительности обслуживания:

- вероятность задержки вызова P{γ>0};

-вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп;

_- вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп;

- среднее время ожидания 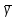для любого поступившего вызова;

- среднее время ожидания 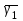для задержанного вызова.

2. Рассчитать среднее число ожидающих вызовов 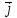(среднюю длину очереди) при показательном распределении длительности обслуживания.

3. По результатам расчетов построить и проанализировать следующие графические зависимости:

- P{γ>t} = f(t) и P₁{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при постоянной длительности обслуживания равна с;

- P{γ>t} = f(t) и P₁{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при показательном распределении длительности обслуживания равна

---

с.

4. Произвести анализ полученных результатов и сделать вывод о характере изменений P{γ>t} и P₁{γ>t}) при увеличении t_доп и с, а также об изменении и с ростом с при прочих равных условиях для различных законов распределения длительности обслуживания.

Значения исходных данных приведены в таблице 1.

Таблица1 – Исходные данные

S	tвх, с	yвх, Эрл	h, с	tдоп1, c	tдоп2, c	tдоп3, c
4	60	80	0,54	0,54	1,62	2,16

Решение

В соответствии с классификацией Кендала процесс обслуживания простейшего потока вызовов полнодоступным пучком линий при показательном распределении длительности обслуживания и неограниченном числе мест для ожидания соответствует математической модели M/М/v, а тот же процесс при постоянной длительности обслуживания вызова – математической модели М/D/v, причем M/М/v описывается вторым распределением Эрланга, а М/D/v описывается кривыми Кроммелина.

Второе распределение Эрланга и характеристики качества прохождения нагрузки имеют следующий вид:



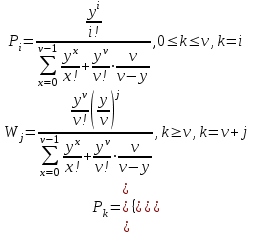
Формулы 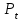и 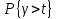табулированы и представлены кривыми Кроммелина.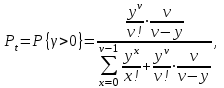





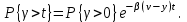
Определение качественных показателей обслуживания управляющими устройствами поступающей нагрузки должно производиться по расчетному значению нагрузки

---

y_р.

Расчетное значение y_р обеспечивает требуемое качество прохождения нагрузки с заданной вероятностью ω, отклоняясь от математического ожидания нагрузки y по экспоненциальному закону



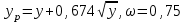
Определим расчетную нагрузку на одно управляющее устройство (маркер) ступени группового искания:

при v = 1, y = c ( 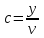) и P{γ>0} = f(c_p)

y_бл = yвх / с = 80/4= 20 Эрл

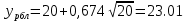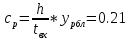Эрл

Эрл

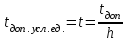
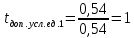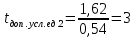Для оценки качественных показателей работы управляющих устройств ступени искания при показательно распределенной и при постоянной длительностях обслуживания необходимо выразить допустимое время ожидания t_доп в условных единицах, численно равных длительности обслуживания маркером одного вызова, в с:



с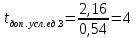

с

с

Далее необходимо вычислить следующие характеристики качества прохождения нагрузки: P{γ>0}, P{γ>t}, P₁{γ>t}= 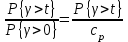с использованием таблиц второй формулы Эрланга и кривых Кроммелина

---

Для математической модели М/М/v:

Вероятность задержки вызова P{γ>0} = с_р=0,21

Вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп равна

Для 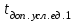Р=0,08987

Для 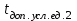Р=0,04037

Для 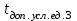Р=0,008152

Вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп равна P₁{γ>t}=

Для

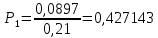
Для

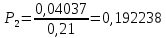
Для

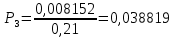
Среднее время ожидания для любого поступившего вызова:

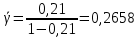с

Среднее время ожидания для задержанного вызова:

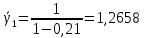с

Среднее число ожидающих вызовов равно

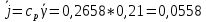Эрл

На основании полученных результатов построим график и график



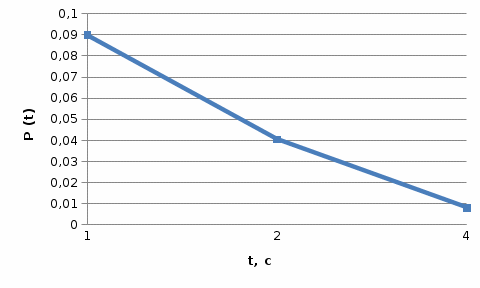
Рисунок 1 - График функции



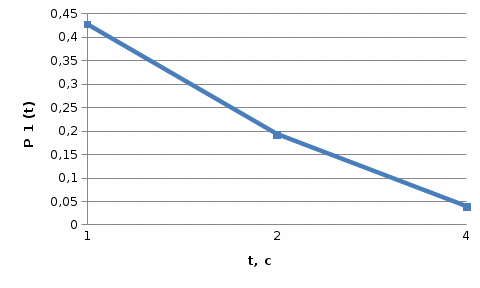
Рисунок 2 - График функции

Для математической модели М/

---

D/v:

Вероятность задержки вызова P{γ>0} = с_р=0,21

Для нахождения вероятности ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп воспользуемся кривыми Кроммелина

Для Р=0,025

Для Р=0,002

Для Р=0



Для

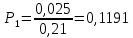
Для

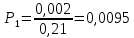
Для

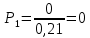
Среднее время ожидания для любого поступившего вызова:

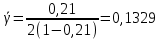с

Среднее время ожидания для задержанного вызова:

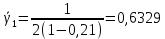с

_{На основании полученных результатов построим график} и график



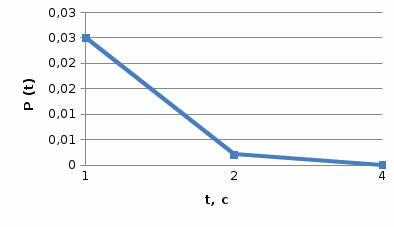
Рисунок 3 - График функции



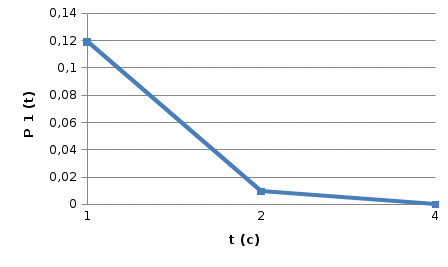
Рисунок 4 - График функции

Вывод

При увеличении 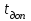в обоих случаях вероятности ожидания обслуживания свыше допустимого времени для любого поступающего и задержанного вызовов снижаются, но в случае с показательным распределением длительности обслуживания вероятность снижается плавно на всей временной оси, а при постоянной длительности занятия сначала резко уменьшается, а потом плавно и медленно уменьшается.

---

Смотрите также файлы

• Сомнения 4 12.docx

• Язык как основное средство человеческого общения.docx

• Отчетность рабочих перед начальниками, начальников перед директором. Премии рабочим за качественную работу.docx

• Основная образовательная программа начального общего образования должна содержать следующие разделы 1 пояснительная записка. Пояснительная записка должна раскрывать 1 цели реализации основной образовательной программы начального общего образования.docx

• Разработка системы мгновенного обмена сообщениями.docx