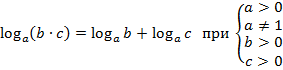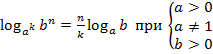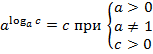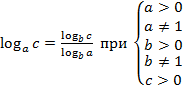Урок по алгебре и началам анализа в 11 классе.

(к учебнику А.Н. Колмогорова)
Тема: Решение логарифмических уравнений и неравенств.
Тип урока: Введение нового материала. (Урок 1)
Цели:

• 
  Познакомить со способами решений логарифмических уравнений.
  
• 
  Отрабатывать умение решать логарифмические уравнения.
  

План урока:

1. 
   Орг. момент 2мин
   
2. 
   Актуализация знаний 3мин
   
3. 
   Введение нового материала 32мин
   
4. 
   Итоги урока 2мин
   
5. 
   Домашнее задание 1мин
   

Ход урока:

1. 
   Орг. момент.
   

Организовать учащихся на лекционное занятие.

Сообщить тему и цель занятия.

Записать число и тему урока.

2. 
   Актуализация знаний
   

Повторить с учащимися основные теоремы о логарифмах.

Основные теоремы о логарифмах.

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   
9. 
   
   

(С 6 по 9 свойство записать в тетради.)

3. 
   Введение нового материала
   

1. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим логарифмическим уравнением служит уравнение вида

---

(где a>0, )
2. Решение логарифмического уравнения вида основано на том, что такое уравнение равносильно уравнению при дополнительных условиях
3. Проверка найденных значений неизвестного по условию уравнения в общем случае является необязательной. Можно выявить посторонние корни и с помощью нахождения области определения исходного уравнения Эта область задается системой неравенств ( ).
4. При решении логарифмических уравнений часто бывает полезен метод введение новой переменной.
5. При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.
6. Решить уравнение.(показать решение)

1) Ответ: 7

2)

Решение:

Ответ: 8

3) Рассмотреть пример 1 на стр. 242 учебника и пример 2 (два способа решения). (самостоятельно)
4) Решить уравнение: (показать решение)

Решение:

---

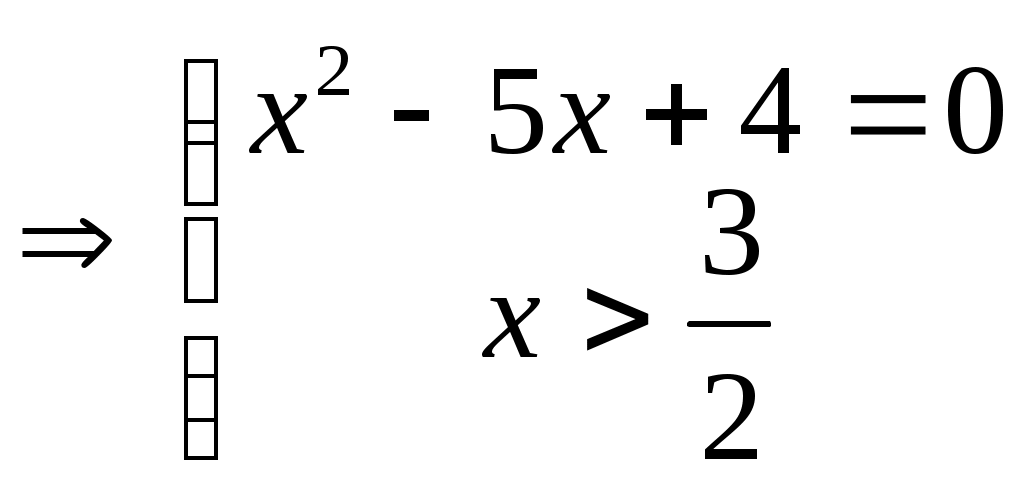
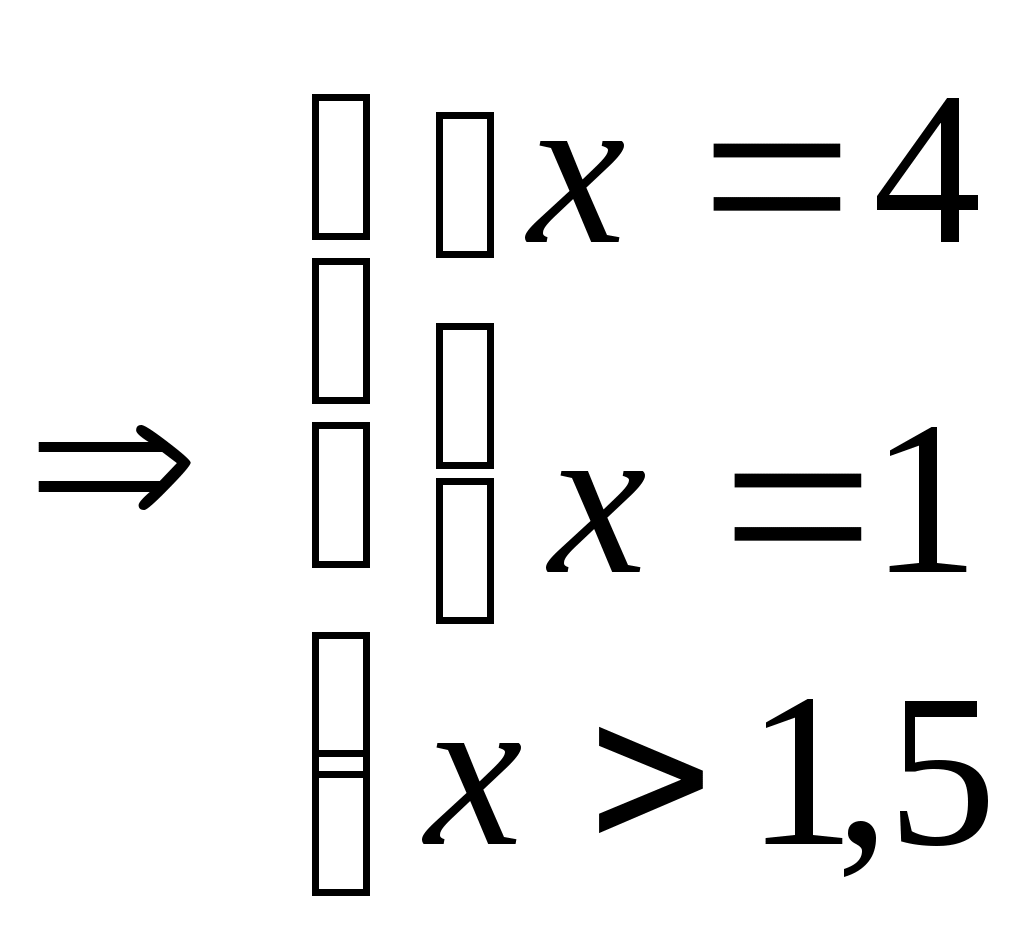
Ответ: 4
5)Решить уравнение: (один ученик у доски)





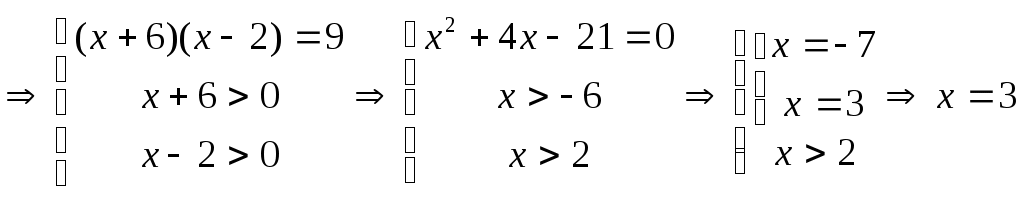Ответ:3
6) Решить уравнение



Решение:

ОДЗ: . Обозначим , получим ;

Если , тогда ; ;

Если , то ; Ответ:
7) по учебнику разобрать примеры 5 и 7 на стр. 243

(самостоятельно)
8) Решить уравнение (совместно)



Решение:

Прологарифмировав обе части уравнения по основанию 2, получим: ;

Обозначим





Значит



Проверка:

1)

---

верно

2) верно

Ответ:

9) Решить уравнение:

Решение:

Перейдем к основанию 5.
, , то
или

Проверка подтверждает что корни данного уравнения.
Ответ: 5; 15
10) Самостоятельно разобрать решение примера 3 на стр.243.

4. 
   Итоги урока
   

Сегодня на уроке мы познакомились со способами решения логарифмических уравнений. Они пригодятся вам на ЕГЭ.

Оценить работу учащихся, выставить отметки.

5. 
   Домашнее задание:
   

п. 39; Решить: №512-515; №519(в,г) №520(в,г).

---

Смотрите также файлы

• Самостоятельная работа мдк 05. 01 Методическое обеспечение образовательного процесса Выполнил студент Бурова Анна.docx

• Практическая работа к теме 1.docx

• Наименование документа, номер, сведения о дате выдачи документа и выдавшем его органе в соответствии с пунктом 4 статьи 9 Федерального закона от 27. 07.docx

• Наблюдение сплошного и линейчатых спектров.docx

• Лекция Субъекты международного частного права 1.pdf