Файл: Задача 2 Решить симплекс методом, контролируя вычисления Двойственная задача имеет вид.docx
Добавлен: 25.04.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача №2
Решить симплекс методом, контролируя вычисления
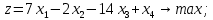
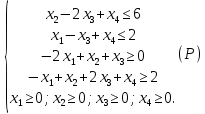
Двойственная задача имеет вид:
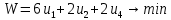
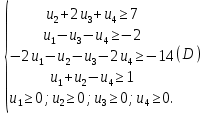
Введем балансовые переменные для пары задач P и D:
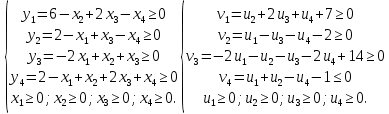
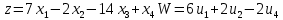
Находим решение, используя алгоритм симплекс метода. Строим исходную симплекс-таблицу.
| | |  |  |  |  | |
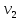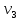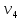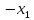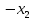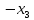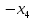| | |  |  |  |  | W = 1 |
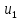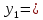 |  | 0 | 1 | -2 | 1 | 6 |
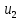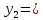 |  | 1 | 0 | -1 | 1 | 2 |
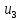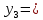 |  | 2 | -1 | -1 | 0 | 0 |
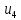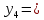 |  | 1 | -1 | -2 | -1 | 2 |
| | Z = 1 | -7 | 2 | 14 | -1 | 0 |
Перейдем к построению оптимального плана. Для того чтобы опорный план был оптимален, при максимизации целевой функции необходимо, чтобы коэффициенты в строке целевой функции были неотрицательными. Т.е. при поиске максимума мы должны освободиться от отрицательных коэффициентов в строке
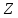и столбца свободных членов.Выберем разрешающий элемент. Выберем столбец с отрицательным коэффициентом в строке целевой функции в качестве разрешающего. Это будет столбец
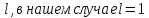.Выберем разрешающую строку, для которой отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально:
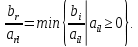
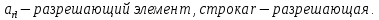
Тогда r = 3. А разрешающий элемент
Выполним шаг жордановых преобразований над симплексной таблицей, который в общем случае можно описать последовательностью действий:
1. На месте разрешающего элемента в новой таблице записывается обратная к нему величина.
2. Все другие элементы разрешающего столбца меняют знак на противоположный и делятся на разрешающий элемент.
3. Все другие элементы разрешающей строки делятся на разрешающий элемент.
4. Все остальные элементы симплексной таблицы вычисляются по следующей формуле:
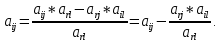
5. Вычеркиваем разрешающий столбец.
Выполним преобразования в соответствии с алгоритмом и получим следующую симплексную таблицу:
| | |  |  |  |  | |
| | |  |  |  |  | W = 1 |
 |  | 0 | 1 | -2 | 1 | 6 |
 |  | 0 | 1/2 | -1/2 | 1 | 2 |
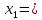 |  | 1 | -1 | -1 | 0 | 0 |
 |  | 0 | -1/2 | -3/2 | -1 | 2 |
| | Z = 1 | 0 | -3/2 | 11,5 | -1 | 0 |
Данное решение не является оптимальным, так как есть отрицательные коэффициенты в строке целевой функции.
Разрешающий элемент теперь
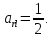
Выполним преобразования в соответствии с алгоритмом и получим следующую симплексную таблицу:
| | | | | | | |
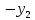| | |  |  | | | W = 1 |
| | | 0 | 0 | -1 | -1 | 0 |
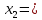| |  | 0 | 1 | -1 | 2 | 4 |
| |  | 1 | 0 | -2 | 2 | 2 |
| | | 0 | 0 | -2 | 2 | 0 |
| | Z = 1 | 0 | 0 | 10 | 2 | 6 |
Т.к. все коэффициенты Z- строки и столбца свободных членов положительны, получено оптимальное решение.
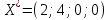и он является оптимальным. 
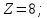Подставим значения x и проверим.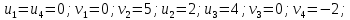
При оптимальном и верном решении Z = W, подставим и проверим:
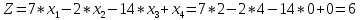
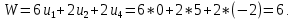
Z = W = 6.
Решение оптимальное и верное.