Файл: Рис. Расчетная схема нижней заправки самолета топливом.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
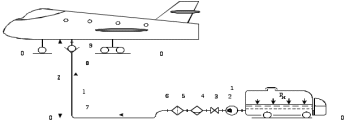Рис. 1. Расчетная схема нижней заправки самолета топливом.1 –цистерна топливозаправщика; 2 – вход в трубопровод; 3 – топливный насос; 4 – кран;
5 – водоотделитель; 6 – фильтр; l – заправочный шланг; 7 – поворот шланга (отвод); 8 – обратный клапан; 9 – заправочная горловина.
Варианты заданий для нижней схемы топливозаправки
| № варианта | Исходные данные | № вари-анта | Исходные данные | ||||||||||||||
| Расход керо-сина Q,м3/час | Темпера-тура керосина t, оС | Высота располо-жения элемента 9(заправоч. горловины) z, м | Высота располо-жения аэродрома Н, м | Расход керо- сина Q,м3/час | Темпе-ратура кероси-на t, оС | Высота распо-ложения элемен-та z, м | Высота располо-жения аэродро-ма, Н, м | ||||||||||
| Внутренний диаметр шланга d = 58 мм | Внутренний диаметр шланга d = 70 мм | ||||||||||||||||
| 1 | 28,8 | -5 | 1,5 | 1550 | 16 | 28,8 | -5 | 1,5 | 1550 | ||||||||
| 2 | 30,06 | -4 | 1,8 | 1500 | 17 | 30,06 | -4 | 1,8 | 1500 | ||||||||
| 3 | 32,4 | -3 | 2,1 | 1450 | 18 | 32,4 | -3 | 2,1 | 1450 | ||||||||
| 4 | 34,2 | -2 | 2,6 | 1400 | 19 | 34,2 | -2 | 2,6 | 1400 | ||||||||
| 5 | 36,0 | 2 | 2,8 | 1350 | 20 | 36,0 | 2 | 2,8 | 1350 | ||||||||
| 6 | 39,6 | 4 | 3,0 | 1300 | 21 | 39,6 | 4 | 3,0 | 1300 | ||||||||
| 7 | 41,4 | 6 | 3,2 | 1250 | 22 | 41,4 | 6 | 3,2 | 1250 | ||||||||
| 8 | 43,2 | 8 | 3,4 | 1200 | 23 | 43,2 | 8 | 3,4 | 1200 | ||||||||
| 9 | 45,0 | 10 | 3,6 | 1150 | 24 | 45,0 | 10 | 3,6 | 1150 | ||||||||
| 10 | 46,8 | 12 | 3,8 | 1100 | 25 | 46,8 | 12 | 3,8 | 1100 | ||||||||
| 11 | 48,6 | 13 | 4,0 | 1000 | 26 | 48,6 | 13 | 4,0 | 1000 | ||||||||
| 12 | 50,4 | 14 | 4,4 | 950 | 27 | 50,4 | 14 | 4,4 | 950 | ||||||||
| 13 | 52,2 | 15 | 4,6 | 900 | 28 | 52,2 | 15 | 4,6 | 900 | ||||||||
| 14 | 54,0 | 16 | 4,8 | 850 | 29 | 54,0 | 16 | 4,8 | 850 | ||||||||
| 15 | 55,8 | 17 | 5,0 | 800 | 30 | 55,8 | 17 | 5,0 | 800 | ||||||||
Характеристики элементов системы нижней заправки
| № элемента на схеме | Наименование элемента | Обозначение | Параметры |
| 1 | Цистерна топливозаправщика | | pН = ? |
| 2 | Вход в трубопровод |  | ζ2 = 0,5 |
| 3 | Насос |  | рпотр. = ? |
| Антикавитационный запас для насоса рнп. = 30 кПа | |||
| 4 | Запорный кран |  | θ = 5о ζ 4 = ? |
| 5 | Водоотделитель |  | ζ 5 = 0,32 |
| 6 | Фильтр | 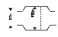 | dф = 5d dс =0,2 мм  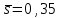 ζ 6 = ? |
| l | Трубопровод (заправочный рукав, шланг) |  | l = 30м l = ? |
| 7 | Изгиб шланга (отвод) |  | θ = 90о R/D = 5 ζ 7 = ? |
| 8 | Обратный клапан | 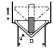 | h/D = 0,4 ζ 8 = ? |
| 9 | Заправочная горловина топливного бака (внезапное расширение) | | ζ 9 = 1,0 |
Оглавление
ВВЕДЕНИЕ 5
1. Теоретические основы расчета гидравлических систем. 6
2. Назначение, состав и принцип действия гидравлических систем 23
3. Методические указания к расчету гидравлических систем 23
3.1. Методика расчета гидравлической системы 23
3.2. Простой трубопровод 25
3.3. Трубопровод с насосной подачей 26
«..ум – это способность из минимума информации выводить максимум заключения, при прочих равных – в кратчайшее время и простейшим анализом
М Веллер «Самовар», с 161.
ВВЕДЕНИЕ
Курсовая работа должна способствовать приобретению знаний и навыков решения задач по разделу механики жидкости и газа – гидравлике. Для гидравлики типичен упрощенный одномерный подход к рассмотрению явлений движения жидкости. Сложный многомерный характер движения жидкости в одномерном рассмотрении учитывается эмпирическими коэффициентами или теоретическими величинами, позволяющими изучать неодномерное движение в одномерной постановке. Спецификой гидравлики является также широкое применение упрощенных и эмпирических методов решения задач с целью получения результатов и методик, удобных, для использования в инженерной практике.
В гидравлике изучают движение капельных жидкостей, то есть таких жидкостей, которые в малых количествах под действием поверхностного натяжения принимают сферическую форму, а в больших – образуют свободную поверхность раздела с газом. Важным свойством капельных жидкостей является то, что они ничтожно мало изменяют свой объем при изменении давления. Поэтому их считают несжимаемыми.
Широкое использование методов гидравлики во многих отраслях техники обусловлено тем, что большинство решений задач, полученных теоретической гидромеханикой, не может быть использовано в инженерной практике. В настоящее время в связи с широким применением численных методов и ЭВМ современная гидравлика представляет механику жидкости, опирающуюся на теоретический фундамент классической гидромеханики. В то же время гидравлика является прикладной наукой, в которой решение доводится до вида, удобного для инженерного применения.
1. Теоретические основы расчета гидравлических систем.
Несмотря на упрощенный подход к решению задач в гидравлике, методика их решения основана на тех же основных законах и уравнениях, которые используются в механике жидкости и газа. Это законы сохранения массы, количества движения и энергии, которые в механике жидкости и газа записываются в виде уравнений неразрывности, движения и энергии. Так как гидравлика рассматривает
одномерное движение несжимаемой жидкости, то уравнения движения и энергии становятся зависимыми, и для решения большинства задач обычно достаточно использовать только два основных уравнений: уравнение неразрывности и уравнение энергии. Все уравнения и зависимости записываются для контрольного объема, представляющего неподвижный в пространстве объем, через который протекает жидкость. Поскольку гидравлическая система представляет в общем случае канал с твердыми стенками, направляющими движение жидкости, в качестве контрольного объема выступает либо вся система в целом, либо ее участок, ограниченный входным 1-1 и выходным 2-2 сечениями (рис.1.1).
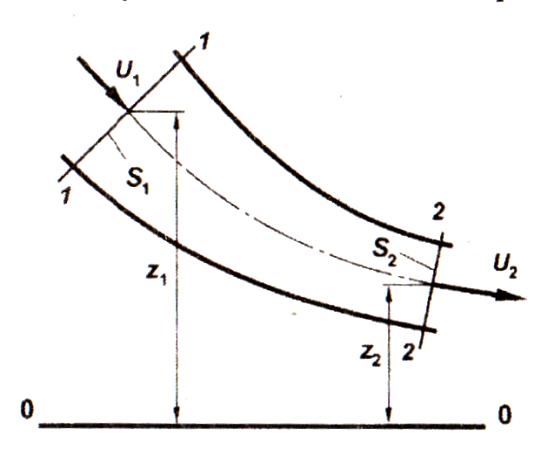
Рис.1.1
Уравнение неразрывности в гидравлике называют уравнением расхода. Для участка системы, ограниченного сечениями 1-1 и 2-2 –контрольного объема (рис.1.1), оно может быть записано в виде:
ρ1u1S1 = ρ2u2S2 (1.1)
или
G = ρuS = const, (1.1а)
где ρ – плотность жидкости (кг/м3), представляющая массу жидкости, заключенную в единице объема; и - среднерасходная скорость жидкости в сечении (м/с); S- площадь поперечного сечения канала (м2); G- массовый расход жидкости (масса жидкости, протекающая через поперечное сечение канала в единицу времени) (кг/с).
Сформулировать уравнение расхода для установившегося (неизменного во времени) течения можно следующим образом: масса жидкости, протекающая в единицу времени через любое поперечное сечение выделенного участка, постоянна.
Для несжимаемой жидкости плотность постоянна в любой точке потока, ввиду чего уравнение неразрывности (расхода) может быть записано:
u1S1 = u2S2(1.2)
или
Q = uS = const, (1.2a)
то есть объем жидкости, протекающий через любое сечение выделенного участка системы в единицу времени, постоянен. Величина Q(м3/с), называется объемным расходом.
Можно отметить, что при использовании понятия объемного расхода уравнение неразрывности для сжимаемой жидкости (1.1) можно записать в таком виде
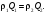(1.1б)Такой вид уравнения неразрывности указывает на то, что при течении сжимаемой жидкости с изменением плотности жидкости изменяется ее объемный расход.