Файл: 10. Вычисление и построение главного вектора и главного момента.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1+ S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
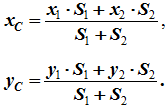
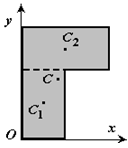
Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
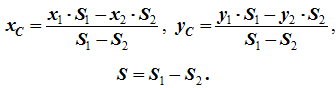
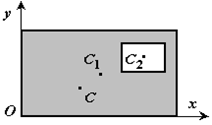
Рисунок 1.9
Центры тяжести простейших фигур
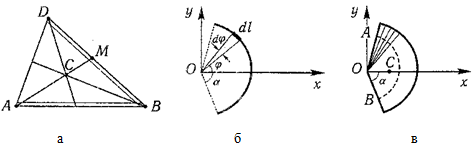
Рисунок 1.10
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB, CM =(1/3)AM.
2 Дуга окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC= 0.
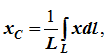
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L =2αR,
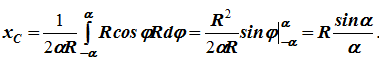
Следовательно:
xC= R(sinα/α).
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
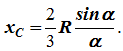
14. Способы задания движения точки.
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.
15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени Δt:
тогда
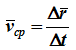
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени
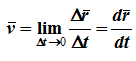
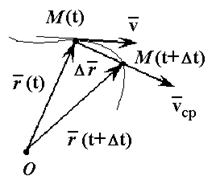
Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
1.3 Ускорение точки
Среднее ускорение
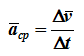
характеризует изменение вектора скорости за малый промежуток времени Δt . Ускорение точки в данный момент времени
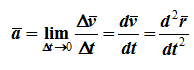
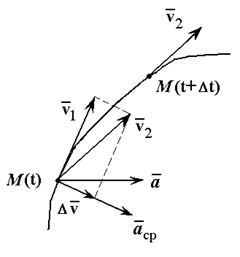
Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.
15. Определение скорости и ускорения при координатном способе задания движения точки.
Связь векторного способа задания движения и координатного дается соотношением
Из определения скорости
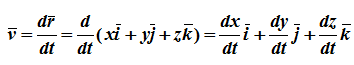
Проекции скорости на оси координат равны производным соответствующих координат по времени:
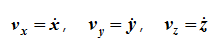
Модуль и направление скорости определяются выражениями
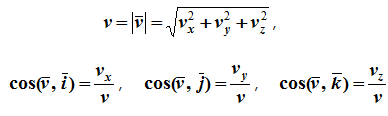
Из определения ускорения
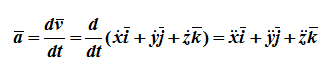
Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени
Модуль и направление ускорения определяются выражениями
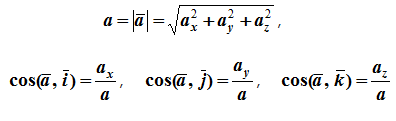
16. Тангенциальное и нормальное ускорение точки.
|
||

