Файл: КУрсовой Проект по дисциплине Конструкции из дерева и пластмасс (наименование учебной дисциплины) на тему Ограждающие и несущие конструкции здания.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

где
 – высота стенки между поясами
– высота стенки между поясами
hв – высота волнистой стенки

При обеспечении устойчивости стенки проверяем ее на срез без учета

Прочность клеевого соединения полки с волнистой стенкой

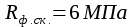

 определяют по глубине паза
определяют по глубине пазаПрогиб балки, нагруженной равномерно распределенной нагрузкой

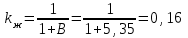
5. Проектирование круглой арки
5.1 Данные для расчёта
Пролет арки
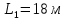 . Шаг конструкции
. Шаг конструкции  .
. Высота арки составит:
 .
. Покрытие - клеефанерные плиты.
Материал арки – сосна 1 сорта.
5.2 Выбор конструктивной схемы
В расчётную схему принимаем трех шарнирную арку.
Радиус кривизны арки определим по формуле:

Центральный угол
 составит:
составит: :
:Длина дуги арки:

5.3 Сбор нагрузок на арку
Определим нормативную и расчётную нагрузки от клеефанерной плиты размерами 6х1м.
Поскольку изменится длинна плиты (по сравнению с плитой, рассчитанной в п. 2), то аналогично табл.1 изменится нагрузка от крепёжных брусков и поперечных рёбер каркаса (п.4 и 6. табл.1):
Табл.2 – Сбор нагрузок на арку от собственного веса плиты 4,5х1.2м
| Вид нагрузки | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке, γf | Расчетная нагрузка, кН/м2 |
| Постоянная нагрузка | |||
| 1. Мягкая черепица KATEPAL 12,3 кг/м2 | 0,123 | 1,05 | 0,129 |
| 2. Фанерные обшивки (δф.в.+δф.н.)·γф=0,105 | 0,105 | 1,1 | 0,116 |
| 3. Продольные ребра каркаса  = ==(0,046·0,196·5·5)/0,98=0,225 | 0,23 | 1,1 | 0,253 |
| 4. Поперечные ребра каркаса  = ==(0,046·0,196·10·5)/5,98=0,075 | 0,075 | 1,1 | 0,082 |
| 5. Утеплитель – минеральная вата на основе базальтового волокна PAROG 37 γ=0,3 кН/м3; tу=50мм;  = ==(0,05·0,098·3·0,3)/0,98=0,045 | 0,045 | 1,2 | 0,054 |
| 6. Крепежные бруски сечением 25×25 мм | 0,069 | 1,1 | 0,076 |
| 7. Пароизоляция FOLIAREX 110 г/м2 | 0,0011 | 1,2 | 0,002 |
| Итого: | 0,65 | – | 0,71 |
Снеговая нагрузка рассчитана ранее в п. 2.3. Рассмотрим снеговую нагрузку в двух вариантах – как равномерно распределённую и треугольную.
Равномерно распределённая нагрузка составит:

Где:
 - коэффициент, определяемый по формуле:
- коэффициент, определяемый по формуле: 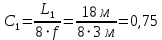 ;
;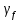 - коэффициент принимаемый 1.6;
- коэффициент принимаемый 1.6;Треугольная нагрузка составит:

Где:
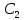 - коэффициент, принимаемый равным
- коэффициент, принимаемый равным 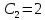
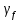 - коэффициент принимаемый 1.6;
- коэффициент принимаемый 1.6;Определим нормативную и расчётную нагрузки от собственного веса арки по формуле:

Где:
 - коэффициент собственного веса арки , принимаемый равным 4.
- коэффициент собственного веса арки , принимаемый равным 4.
| Табл. 3 – Сбор нагрузок на арку | ||
| Вид нагрузки | Постоянная | Снеговая |
| Нормативная | 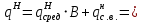  | Равномерно распределённая: 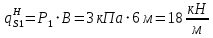 Треугольная:  |
| Расчётная | 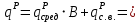  (B – грузовая ширина арки, равная шагу арок, 6м.) | Равномерно распределённая:  Треугольная:  ( (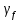 - коэффициент надёжности по снеговой нагрузке, принимаемый равным 1.4 согласно п. 10.12[2]) - коэффициент надёжности по снеговой нагрузке, принимаемый равным 1.4 согласно п. 10.12[2]) |
5.4 Статический расчёт арки
Рассчитываем арку на следующие сочетания нагрузок:
-
Постоянная + снеговая равномерно распределённая нагрузка по всему пролёту; -
Постоянная по всему пролёту + снеговая равномерно распределённая по длине равной половине пролёта. -
Постоянная по всему пролёту + снеговая по треугольной эпюре на половине пролёта
Сочетание 1 (
 ). Опорные реакции от постоянной расчётной нагрузки:
). Опорные реакции от постоянной расчётной нагрузки:Сочетание 1 (
 ). Опорные реакции от постоянной расчётной нагрузки:
). Опорные реакции от постоянной расчётной нагрузки:

Опорные реакции от снеговой расчётной нагрузки:


Суммарные усилия от совместного действия постоянной и снеговой нагрузок:


Сочетание 2 (
 ). Опорные реакции от постоянной расчётной нагрузки аналогичны сочетанию 1.
). Опорные реакции от постоянной расчётной нагрузки аналогичны сочетанию 1. Опорные реакции от снеговой расчётной нагрузки:


Суммарные усилия от совместного действия постоянной и снеговой нагрузок:

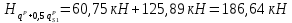
Наибольший изгибающий момент в сечении при
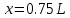 :
:


Сочетание 3 (
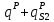 ). Опорные реакции от постоянной расчётной нагрузки аналогичны сочетанию 1. Опорные реакции от снеговой треугольной расчётной нагрузки составят:
). Опорные реакции от постоянной расчётной нагрузки аналогичны сочетанию 1. Опорные реакции от снеговой треугольной расчётной нагрузки составят:

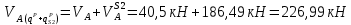

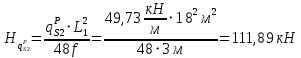

Суммарные усилия от совместного действия постоянной и снеговой нагрузок:


Наибольший изгибающий момент в сечении при
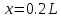 :
:
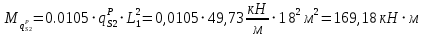

Наибольший изгибающий момент в сечении при
 :
: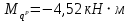
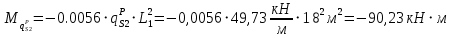

Для этих сечений определим продольные усилия. Для сечения при
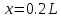 :
: 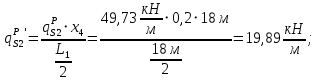




 Для сечения при
Для сечения при  :
: 

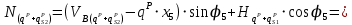
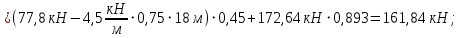 На опорном шарнире усилия составят:
На опорном шарнире усилия составят: