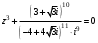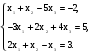ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задания для контрольной работы
Задание 1
Найти сумму, произведение и частное чисел
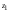 и
и 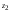 .
.Вариант 10
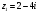 ,
, 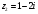 .
.Решение:
-
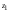 +
+ 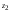 = 2 - 4i + 1 - 2i = 3 – 6i
= 2 - 4i + 1 - 2i = 3 – 6i -
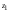 *
* 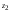 = (2 - 4i)(1 - 2i) = (2 – 4i)+(-4i + 8i) = 2 + 8i
= (2 - 4i)(1 - 2i) = (2 – 4i)+(-4i + 8i) = 2 + 8i -
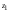 /
/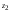 = (2 - 4i) / (1 - 2i) = (2 - 4i)(1 + 2i)/ (1 - 2i)(1 + 2i) = 10/5 = 2
= (2 - 4i) / (1 - 2i) = (2 - 4i)(1 + 2i)/ (1 - 2i)(1 + 2i) = 10/5 = 2
Задание 2
Решить уравнения.
Вариант 10 а) z2 + 4z + 17 = 0; б)
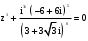 .
.Решение:
-
z2 + 4z + 17 = 0
D = 42 – 68 = -52
Ответ: не имеет корней
z =
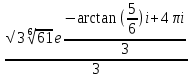
z =
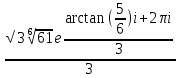
z =
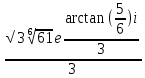
Задание 3
Даны матрицы
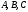 и числа
и числа  и
и 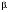
Найти
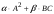 .
.Вариант 10
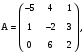
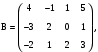
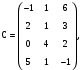
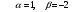 .
.A2=
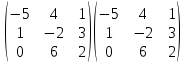 =
= 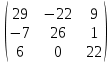
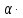 A2 =
A2 =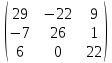
 1=
1= 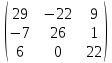
BC =
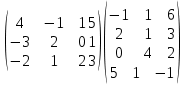 =
= 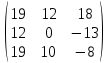
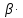 BC = -2
BC = -2 
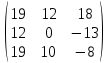 =
= 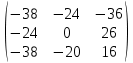
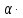 A2 +
A2 + 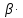 BC =
BC = 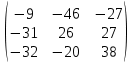
Задание 4
Решить систему уравнений:
а) по правилу Крамера;
б) методом Гаусса;
в) матричным методом.
Вариант 10
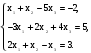
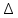 =
= 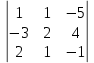 = 34
= 34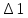 =
= 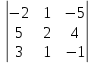 = 34
= 34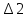 =
= 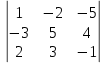 = 68
= 68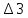 =
= 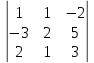 = 34
= 34Ответ:
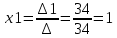
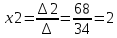
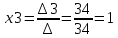
Перепишем систему уравнений в матричном виде и решим его методом Гаусса
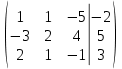
К 2 строке добавляем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 2
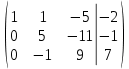
2-ю строку делим на 5
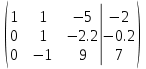
От 1 строки отнимаем 2 строку, умноженную на 1; к 3 строке добавляем 2 строку, умноженную на 1
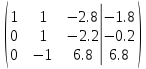
3-ю строку делим на 6.8
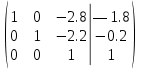
К 1 строке добавляем 3 строку, умноженную на 2.8; к 2 строке добавляем 3 строку, умноженную на 2.2
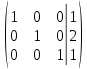
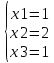
Ответ:
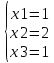
A =
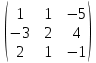
B =

X =
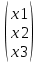
A
 X = B, значит X = A-1
X = B, значит X = A-1  B
BX = A-1
 B =
B = 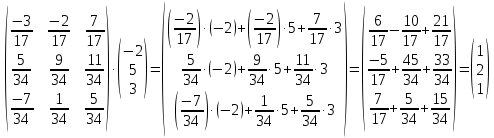
Ответ:
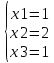
Задание 5
Даны вершины пирамиды ABCDи точка
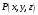 .
. Найти:
а) длину ребра АС;
б) косинус угла между ребрами АВ и СD;
в) площадь грани АВС;
г) объем пирамиды;
д) уравнение прямой, на которой лежит ребро АВ;
е) уравнение прямой, на которой лежит высота
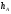 пирамиды, опущенная из вершины А.
пирамиды, опущенная из вершины А.Выяснить, лежат ли точки
 и
и  по одну сторону плоскости грани
по одну сторону плоскости грани 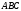 или по разные?
или по разные?Вариант 1
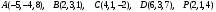 ..
..Вариант 2
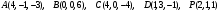 .
.Вариант 3
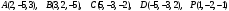 .
.Вариант 4
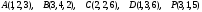 .
.Вариант 5
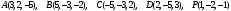 .
. Вариант 6
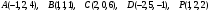
.
Вариант 7
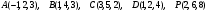 .
.Вариант 8
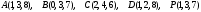 .
.Вариант 9
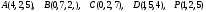
Вариант 10
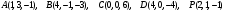 .
.Задание 6
Даны векторы
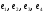 и
и  в стандартном базисе пространства
в стандартном базисе пространства 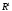 .
.Требуется:
а) убедиться, что векторы
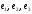 и
и 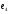 образуют базис пространства
образуют базис пространства 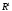 ;
;б) найти разложение вектора
 по этому базису;
по этому базису;в) найти угол между векторами
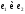 .
.Вариант 1
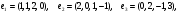
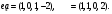
Вариант 2
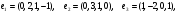
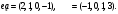
Вариант 3
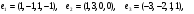

Вариант 4
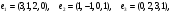
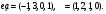
Вариант 5
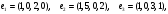
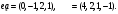
Вариант 6
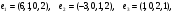
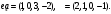
Вариант 7
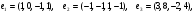
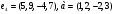 .
.Вариант 8
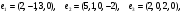
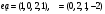 .
.Вариант 9
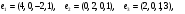
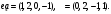
Вариант 10
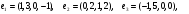
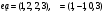 .
.
Задание 7
Найти собственные значения и собственные векторы линейного оператора, заданного в базисе
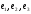 следующей матрицей.
следующей матрицей.Вариант 1
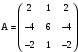 . Вариант 2
. Вариант 2 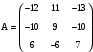 .
.Вариант 3
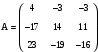 . Вариант 4
. Вариант 4 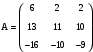 .
.Вариант 5
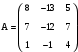 . Вариант 6
. Вариант 6 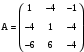 .
.Вариант 7
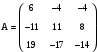 . Вариант 8
. Вариант 8 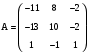 .
.Вариант 9
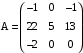 . Вариант 10
. Вариант 10 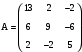 .
.Решение нулевого варианта контрольных работ
Задание 1
Найдите сумму, произведение и частное комплексных чисел
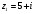 ,
, 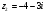 .
.Решение
Если
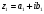 ,
, 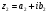 , то:
, то: 1)
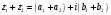 .
.Для решаемой задачи
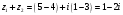 .
. 2)
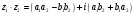 .
. Практически комплексные числа, заданные в алгебраической форме, перемножаются как многочлены с учетом того, что
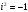 . Для решаемой задачи
. Для решаемой задачи 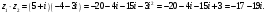
3)
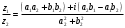 .
.Практически деление комплексных чисел удобнее выполнять следующим образом
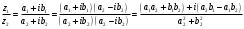 .
.Для решаемой задачи
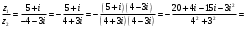
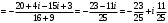 .
.Задание 2
Решить уравнения: а)
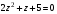 ; б)
; б)