ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Уравнение плоскости BCD найдём, используя уравнение плоскости, проходящей через три заданные точки

 :
:  .
.Для решаемой задачи это точки
 ,
, 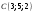 ,
, 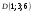 и, следовательно, уравнение АВС имеет вид:
и, следовательно, уравнение АВС имеет вид: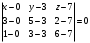 ,
,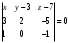 ,
, 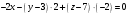 ,
,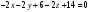 ,
, .
.Вектор
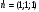 является нормальным вектором плоскости
является нормальным вектором плоскости 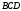 , следовательно, этот вектор является направляющим вектором для прямой, проходящей через точку
, следовательно, этот вектор является направляющим вектором для прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 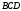 . Уравнение этой прямой
. Уравнение этой прямой 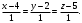
Выясним, лежат ли точки
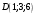 и
и 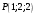 по одну сторону плоскости грани
по одну сторону плоскости грани 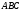 или по разные?
или по разные?Найдём уравнение плоскости грани
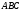 как уравнение плоскости, проходящей через точку
как уравнение плоскости, проходящей через точку 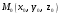 и имеющей нормальный вектор
и имеющей нормальный вектор 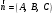 :
: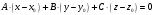 .
.Для решаемой задачи
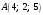 , а
, а 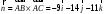 найден в п. в) решаемой задачи. Следовательно, уравнение плоскости грани
найден в п. в) решаемой задачи. Следовательно, уравнение плоскости грани 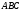
:
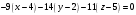 или
или 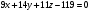 .
.Для всех точек
 , лежащих на плоскости, будет выполняться равенство
, лежащих на плоскости, будет выполняться равенство 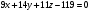 , для точек, лежащих по одну сторону плоскости, будет выполняться неравенство
, для точек, лежащих по одну сторону плоскости, будет выполняться неравенство 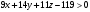 , для точек, лежащих по другую сторону плоскости, - неравенство
, для точек, лежащих по другую сторону плоскости, - неравенство  .
.Для точки
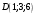 выполняется неравенство
выполняется неравенство 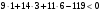 .
.Для точки
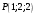 выполняется неравенство
выполняется неравенство 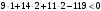 .
.Следовательно, точки
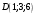 и
и 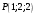 лежат по одну сторону плоскости грани
лежат по одну сторону плоскости грани 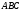 .
.Задание 6
В стандартном базисе пространства
 даны векторы
даны векторы 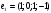 ,
,  ,
, 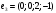 ,
,  и
и 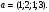
Требуется:
а) убедиться, что векторы
 образуют базис пространства
образуют базис пространства  ;
;б) найти разложение вектора
 по этому базису;
по этому базису;в) найти угол между векторами
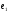 и
и 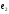 .
.Решение
а) Векторы
 образуют базис пространства
образуют базис пространства  , если их линейная комбинация
, если их линейная комбинация  равна нулю только при
равна нулю только при 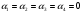 .
.Уравнению
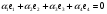
соответствует система уравнений

Эта однородная система имеет только нулевое (тривиальное) решение
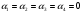 , если её определитель не равен нулю, то есть
, если её определитель не равен нулю, то есть 
Вычислим определитель, разложив его по элементам второй строки:
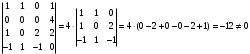 .
.Следовательно, заданные векторы
 образуют базис пространства
образуют базис пространства  .
.б) Найдем координаты вектора
 в базисе
в базисе  из векторного уравнения
из векторного уравнения 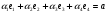 .
.Этому векторному уравнению соответствует система
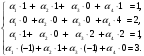
Решив систему, находим

 .
.Следовательно, разложение вектора
 по базису
по базису  :
: 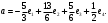
в) Если скалярное произведение в
 определено аналогично тому, как это было в
определено аналогично тому, как это было в  , то
, то 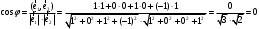 .
.Следовательно,
 , то есть векторы
, то есть векторы 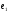 и
и 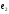 ортогональны.
ортогональны.Задание 7
Найти собственные значения и собственные векторы линейного оператора, заданного в базисе
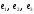 матрицей
матрицей 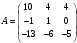 .
.Решение
Ненулевой вектор
 называется собственным вектором, а число
называется собственным вектором, а число  -соответствующим вектору
-соответствующим вектору  собственным значением оператора
собственным значением оператора
 , если
, если 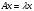 или
или 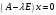 .
.Для заданной матрицы
 последнее матричное уравнение примет вид
последнее матричное уравнение примет вид 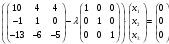 или
или  .
.Этому матричному уравнению соответствует однородная линейная система уравнений
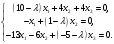
Для того, чтобы однородная система имела ненулевые решения необходимо, чтобы её определитель
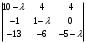 был равен нулю.
был равен нулю.Уравнение
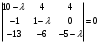 называют
называют характеристическим уравнением.
Для нахождения собственных значений
 решим характеристическое уравнение:
решим характеристическое уравнение: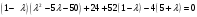 ;
;  ;
; 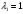 ,
,  ,
,  .
.Таким образом, собственными значениями линейного оператора, заданного матрицей
 (собственными значениями матрицы
(собственными значениями матрицы  ), являются
), являются 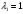 ,
,  ,
,  .
.Найдем собственные векторы, соответствующие этим собственным значениям, то есть векторы
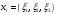
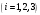 .
.Для
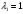 получим систему уравнений для нахождения координат первого собственного вектора
получим систему уравнений для нахождения координат первого собственного вектора 


Полагая
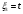 , получим координаты первого собственного вектора
, получим координаты первого собственного вектора
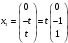 . При
. При  , получим
, получим 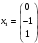 .
.Для
 получим систему уравнений для нахождения координат второго собственного вектора
получим систему уравнений для нахождения координат второго собственного вектора 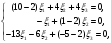

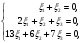
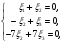

Полагая
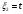 , получим координаты второго собственного вектора
, получим координаты второго собственного вектора  . При
. При  , получим
, получим  .
.Для
 получим систему уравнений для нахождения координат третьего собственного вектора
получим систему уравнений для нахождения координат третьего собственного вектора 

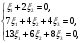


Полагая
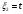 , получим координаты третьего собственного вектора
, получим координаты третьего собственного вектора 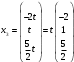 . При
. При 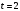 , получим
, получим 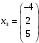 .
.


