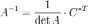Файл: М инистерство науки и высшего образования рф.docx

М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ

Кубанский казачий государственный институт пищевой индустрии и бизнеса (филиал) федерального государственного бюджетного образовательного учреждения высшего образования

«Московский государственный университет технологий и

управления им. КГ. Разумовского (Первый казачий университет)»

Кафедра: «Технологического менеджмента и социально-экономических дисциплин»

РЕФЕРАТ

По дисциплине «Высшая математика»  

Выполнил студент Д.В. Гагин

1   курса ПАС - 22030 спец.(напр) 27.03.04

Шифр 22/10638

Проверил: ст. преподаватель Е.Б. Маринкин

Темрюк 2023 г.

На тему: Обратная матрица

План:матрица обратный итерационный

Введение

1. Свойства обратной матрицы

2. Способы нахождения обратной матрицы

2.1 Точные (прямые) методы

2.2 Итерационные методы

3. Примеры

Примечания

Введение

Обратная матрица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:


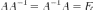
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

1. Свойства обратной матрицы

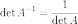, где 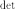обозначает определитель.

для любых двух обратимых матриц A и B.

---

где * T обозначает транспонированную матрицу.

для любого коэффициента .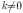

Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{- 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

2. Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

2.1 Точные (прямые) методы

Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ_i (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
.

.
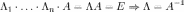Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n³).

С помощью союзной матрицы

C ^{* T} — транспонированная союзная матрица;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
Использование LU/LUP-разложения

Матричное уравнение AX = I_n для обратной матрицы X можно рассматривать как совокупность n систем вида Ax = b. Обозначим i-ый столбец матрицы X через X_i; тогда AX_i = e_i, 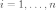,поскольку i-м столбцом матрицы

---

I_n является единичный вектор e_i. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA = LU. Пусть PA = B, B ^{− 1} = D. Тогда из свойств обратной матрицы можно записать: D = U ^{− 1}L ^{− 1}. Если умножить это равенство на U и L то можно получить два равенства вида UD = L ^{− 1} и DL = U ^{− 1}. Первое из этих равенств представляет собой систему из n² линейных уравнений для 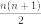из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для 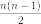из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство A ^{− 1} = DP. В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

2.2 Итерационные методы

Методы Шульца

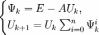
Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения 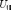в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору 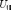, обеспечивающие выполнение условия 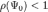(спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы

---

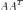(а именно, если A — симметричная положительно определённая матрица и 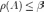, то можно взять 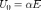, где 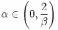; если же A — произвольная невырожденная матрица и 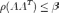, то полагают 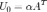, где также 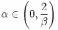; можно конечно упростить ситуацию и, воспользовавшись тем, что 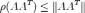, положить ). Во-вторых, при таком задании начальной матрицы нет гарантии, что 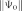будет малой (возможно, даже окажется 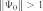), и высокий порядок скорости сходимости обнаружится далеко не сразу.

3. Примеры

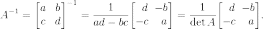
Обращение матрицы 2х2 возможно только при условии, что .

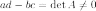Задание. Матричным способом решить систему линейных алгебраических уравнений (СЛАУ) {x+2·y+3·z=04·x+(-y)+23·z=53·x+y+2·z=6

Решение:

Находим обратную к (1234-123312). Вычисляем определитель

|1234-123312| = 1 · (-1) · 2 + 2 · 23 · 3 + 4 · 1 · 3 - 3 · (-1) · 3 - 2 · 4 · 2 - 23 · 1 · 1 = (-2) + 138 + 12 - (-9) - 16 - 23 = 118

Вычисляем миноры Mij и алгебраические дополнения Aij всех элементов таблицы.

|-12312| = -1 · 2 - 23 · 1 = -2 - 23 = -25

M11=-25, A11=-25,

|2312| = 2 · 2 - 3 · 1 = 4 - 3 = 1

M21=1, A21=-1,

|23-123| = 2 · 23 - 3 · (-1) = 46 - (-3) = 49

M31=49, A31=49,

|42332| = 4 · 2 - 23 · 3 = 8 - 69 = -61

M12=-61, A12=61,

|1332| = 1 · 2 - 3 · 3 = 2 - 9 = -7

M22=-7, A22=-7,

|13423| = 1 · 23 - 3 · 4 = 23 - 12 = 11

M32=11, A32=-11,

|4-131| = 4 · 1 - (-1) · 3 = 4 - (-3) = 7

M13=7, A13=7,

|1231| = 1 · 1 - 2 · 3 = 1 - 6 = -5

M23=-5, A23=5,

|124-1| = 1 · (-1) - 2 · 4 = -1 - 8 = -9

M33=-9, A33=-9,

обратная матрица равна 1118(-25-14961-7-1175-9).

Умножаем присоединенную матрицу на столбец свободных коэффициентов (-25-14961-7-1175-9) · (056) = (289-101-29)

В ходе вычислений были выполнены следующие действия

Умножаем 1 строку на 1 столбец (-25) · 0 + (-1) · 5 + 49 · 6 = 289

Умножаем 2 строку на 1 столбец 61 · 0 + (-7) · 5 + (-11) · 6 = -101

Умножаем 3 строку на 1 столбец 7 · 0 + 5 · 5 + (-9) · 6 = -29

Делим произведение на определитель основной матрицы системы и записываем ответ.

---

Ответ: (289118;-101118;-29118)

Примечание

1. 
    Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, — М.: Вильямс, 2006 (с. 700).
   
2. 
   ↑ Petković, M. D. Generalized Schultz iterative methods for the computation of outer inverses (англ.) // Computers & Mathematics with Applications. — 2014. — June (vol. 67, iss. 10). — P. 1837—1847. — doi:10.1016/j.camwa.2014.03.019.
   
3. 
   ↑ Pan, V., Reif, J. Fast and efficient parallel solution of dense linear systems (англ.) // Computers & Mathematics with Applications. — 1989. — Vol. 17, iss. 11. — P. 1481—1491. — doi:10.1016/0898-1221(89)90081-3.
   

---