Файл: Контрольная работа по дисциплине Информатика 1 семестр Вариант 1 Проверил Чита 2022 содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Забайкальский государственный университет»
(ФГБОУ ВО «ЗабГУ»)
Энергетический факультет
Кафедра Прикладной информатики и математики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Информатика»
1 семестр
Вариант № 1
Выполнил:
Проверил:
Чита 2022
СОДЕРЖАНИЕ
| 3 |
| 13 |
| 31 |
| 32 |
| Список использованных источников…………………………………….. | 34 |
-
Подходы к измерению количества информации
(алфавитный, вероятностный, семантический). Примеры решения задач
Рассмотрим два подхода к измерению информации – содержательный
(вероятностный) и символьный (алфавитный).
В содержательном подходе возможна качественная оценка информации: новая, срочная, важная и т. д. Согласно К. Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией – той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации. Неопределенность некоторого события – это количество возможных исходов данного события. Например, неопределенность погоды на завтра обычно заключается в диапазоне температуры воздуха и возможности выпадения осадков.
Содержательный подход часто называют субъективным, так как разные
люди (субъекты) информацию об одном и том же предмете оценивают по-разному. Но если число исходов не зависит от суждений людей (например, случай бросания кубика или монеты), то информация о наступлении одного из
возможных исходов является объективной.
Формулу для вычисления количества информации, учитывающую неодинаковую вероятность событий, предложил К. Шеннон в 1948 г. Количественная зависимость между вероятностью события р и количеством информации I в сообщении о нем выражается формулой Шеннона (1):
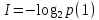
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить следующим образом: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Количество информации для событий с различными вероятностями определяется по формуле, также названной формулой Шеннона (2):
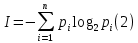
Рассмотрим пример. В коробке имеется 100 шаров. Из них 80 белых и 20
черных. Очевидно, вероятность того, что при вытаскивании случайным образом попадется белый шар, больше, чем вероятность попадания черного. Проведем количественную оценку вероятности для каждой ситуации. Обозначим
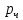 – вероятность, что вытащили черный шар,
– вероятность, что вытащили черный шар, 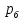 – вероятность, что вытащили белый шар. Тогда:
– вероятность, что вытащили белый шар. Тогда: 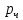 = 20/100 = 0,2,
= 20/100 = 0,2, 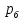 = 80/100 = 0,8. Заметим, что вероятность попадания белого шара в 4 раза больше, чем черного.
= 80/100 = 0,8. Заметим, что вероятность попадания белого шара в 4 раза больше, чем черного.Количество информации в сообщении, что вынутый случайным образом шар является черным, вычисляется по формуле (3):
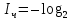 (0,2) =2,321928 бит. (3)
(0,2) =2,321928 бит. (3)Количество информации в сообщении, что вынутый случайным образом
шар является белым, вычисляется по формуле (4):
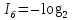 (0,8)=0,321928 бит. (4)
(0,8)=0,321928 бит. (4)Количество информации в сообщении о цвете вынутого случайным образом шара вычисляется по формуле (5):
–0,2
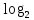 (0,2)-0,8
(0,2)-0,8 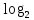 (0,8)=0,2*2,321928+0,8*0,321928=0,721928 бит. (5)
(0,8)=0,2*2,321928+0,8*0,321928=0,721928 бит. (5)Если события равновероятны (
 = 1/N, где N – число возможных событий), то величина количества информации I вычисляется по формуле Р. Хартли (6):
= 1/N, где N – число возможных событий), то величина количества информации I вычисляется по формуле Р. Хартли (6):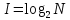 (6)
(6)Используя формулу (6), можно записать и формулу, которая связывает количество возможных событий N и количество информации I (7)
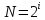 (7)
(7)-
Алфавитный подход.
Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита. С позиций информатики носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Информативность последовательности символов зависит не от содержания сообщения, а определяется минимально необходимым количеством символов для кодирования этой последовательности символов. Алфавитный подход является объективным, т. е. он не зависит от субъекта, воспринимающего сообщение. Смысл сообщения либо учитывается на этапе выбора алфавита кодирования, либо не учитывается вообще.
При алфавитном подходе, если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ (информационный вес одного символа), вычисляется по формуле (6), где N – мощность алфавита (полное количество символов, составляющих алфавит выбранного кодирования). Тогда мощность алфавита можно вычислить по формуле (7).
В стандартную кодовую таблицу (например, ASCII) помещаются все необходимые символы: английские и русские прописные и строчные буквы, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр. В двоичном коде один двоичный разряд несет одну единицу информации, которая называется 1 бит.
В алфавите, который состоит из двух символов (двоичное кодирование),
каждый символ несет 1 бит (
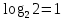 ) информации; из четырех символов –
) информации; из четырех символов –каждый символ несет 2 бита информации (
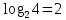 ); из восьми символов –
); из восьми символов –3 бита (
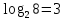 ) и т. д. Один символ из алфавита мощностью 256 несет в тексте 8 битов (
) и т. д. Один символ из алфавита мощностью 256 несет в тексте 8 битов (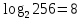 ) информации.
) информации. 1 байт =8 битов
Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста.
Для измерения информации используются и более крупные единицы:
Наряду с байтами для измерения количества информации используются более крупные единицы:
1 Килобайт (Кбайт) = 1024 байт =
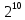 байт =
байт =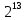 бит;
бит;1 Мегабайт (Мбайт) = 1024 Кбайт =
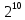 Кбайт =
Кбайт = 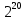 байт =
байт = 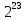 бит;
бит;1 Гигабайт (Гбайт) =1024 Мбайт =
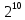 Мбайт =
Мбайт = 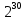 байт =
байт =  бит;
бит;1 Терабайт (Тбайт) = 1024 Гбайт =
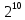 Гбайт =
Гбайт = 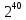 байт =
байт =  бит;
бит;1 Петабайт (Пбайт) = 1024 Тбайт =
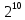 Тбайт =
Тбайт = 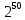 байт =
байт = 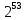 бит;
бит;1 Эксабайт (Эбайт) = 1024 Пбайт =
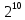 Пбайт =
Пбайт = 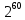 байт =
байт =  бит.
бит.Единицы измерения количества информации, в названии которых есть приставки «кило», «мега» и т. д., с точки зрения теории измерений не являются корректными, поскольку эти приставки используются в метрической системе мер, в которой в качестве множителей кратных единиц используется коэффициент 10, где n=3,6,9 и т. д.
Для устранения этой некорректности Международная электротехническая комиссия, занимающаяся созданием стандартов для отрасли электронных технологий, утвердила ряд новых приставок для единиц измерения количества информации: киби (kibi), меби (mebi), гиби (gibi), теби (tebi), пети (peti), эксби (exbi). Однако пока используются старые обозначения единиц измерения количества информации, и требуется время, чтобы новые названия начали широко применяться.
Последовательность действий при переводе одних единиц измерения информации в другие приведена на следующей схеме (Рисунок 1):
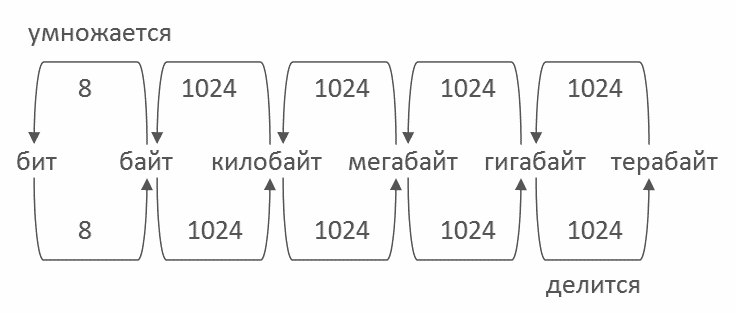
Рисунок 1 – Перевод единиц измерения информации.
Если весь текст состоит из k символов, то при алфавитном подходе размер содержащейся в нем информации H определяется по формуле (8):
H = k · I, (8)
где I – информационный вес одного символа в используемом алфавите.
Максимальное количество слов L из m букв, которое можно составить из алфавита мощностью N, определяется по формуле (9):
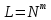 (9)
(9)Зная, что
 , данную выше формулу можно представить в другом виде:
, данную выше формулу можно представить в другом виде:если количество символов алфавита равно N, а количество символов в записи сообщения – K, то информационный объем V данного сообщения вычисляется по формуле:
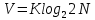 (10)
(10)При алфавитном подходе к измерению информации информационный объем текста зависит только от размера текста и от мощности алфавита, а не от содержания. Поэтому нельзя сравнивать информационные объемы текстов, написанных на разных языках, по размеру текста.
Пример:
1. Считая, что каждый символ кодируется одним байтом, оцените информационный объем следующего предложения: Белеет Парус Одинокий В Тумане Моря Голубом!
Решение.
Так как в предложении 44 символа (считая знаки препинания и пробелы), то информационный объем вычисляется по формуле:
V=44⋅1 байт=44 байта=44⋅8 бит=352 бита
2. Объем сообщения равен 11 Кбайт. Сообщение содержит 11264 символа. Какова мощность алфавита?
Решение.
Выясним, какое количество бит выделено на 1 символ. Для этого переведем объем сообщения в биты:
11 Кбайт=11⋅210 байт=11⋅210⋅23 бит=11⋅213 бит и разделим его на число символов.
На 1 символ приходится: (11⋅213)/11264=(11⋅213)/(11⋅210)=23=8 бит.
Мощность алфавита определяем из формулы Хартли: N=28=256 символов.

