Файл: Одномерная линейная регрессия и корреляция по дисциплине моделирование процессов и объектов в металлургии.docx
Добавлен: 28.04.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Необходимо оценить тесноту линейной корреляционной связи между содержанием никеля (X) и твердостью чугуна (Y); определить коэффициенты уравнения линейной регрессии, их погрешность и статистическую значимость; оценить качество аппроксимации экспериментальных данных полученным линейным уравнением регрессии по диаграмме рассеяния.
На основании полученных данных в ходе замеров произведём регрессионный анализ
Результаты регрессионной статистики представим в таблице 1
Таблица 1
| Регрессионная статистика | |
| Множественный R | 0,768058439 |
| R-квадрат | 0,589913765 |
| Нормированный R-квадрат | 0,555739912 |
| Стандартная ошибка | 2,977528143 |
| Наблюдения | 14 |
| | |
Результаты дисперсионного анализа представим в таблице 2
Таблица 2
| | df | SS | MS | F | Значимость F |
| Регрессия | 1 | 153,0404853 | 153,0404853 | 17,262138 | 0,001335 |
| Остаток | 12 | 106,3880861 | 8,865673841 | | |
| Итого | 13 | 259,4285714 | | | |
Результаты ошибки приведены в таблице 3
Таблица 3
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 54,4293433 | 4,912817322 | 11,07904889 | 1,17107E-07 | 43,72523 | 65,13345 | 43,72523 | 65,13345 |
| Переменная X 1 | 6,262251694 | 1,507242831 | 4,154772918 | 0,001335176 | 2,978252 | 9,546252 | 2,978252 | 9,546252 |
На основании исходных данных построим диаграмму рассеяния.
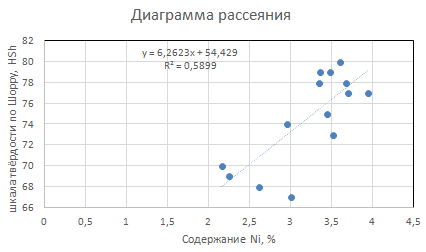
Проверка модели по коэффициентам R1 и R2 показывает, что переменные имеют строгую положительную корреляцию.
Далее проверим значимость по критерию Фишера
F=17,26; Fкр=4,75; Значит гипотезу о равенстве 0 коэффициентов b0 и b1 отвергаем, данная модель может быть использована для прогнозирования твёрдости по Шорру от процентного содержания Ni.
Далее проверяем значимость отдельных параметров модели по значениям t-статистики. Для сравнения берём данные коэффициента tb0 = 11,08 и tb1 = 4,15. Рассчитаем tкр =2,18.
Коэффициенты значимы.
Уравнение регрессии:
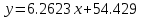
Далее в таблице 4 представим разницу между значениями измерений и результатами расчётов, а так же показатель абсолютной ошибки в процентном соотношении.
Таблица 4
| Ni,% | HSh, ед. измеренное | HSh, ед. расчётное | Ошибка, % |
| 3,68 | 78 | 77,474264 | 0,674020513 |
| 3,7 | 77 | 77,59951 | 0,778584416 |
| 3,44 | 75 | 75,971312 | 1,295082667 |
| 3,48 | 79 | 76,221804 | 3,516703797 |
| 2,16 | 70 | 67,955568 | 2,920617143 |
| 2,25 | 69 | 68,519175 | 0,696847826 |
| 3,34 | 78 | 75,345082 | 3,403741026 |
| 3,36 | 79 | 75,470328 | 4,467939241 |
| 2,95 | 74 | 72,902785 | 1,482722973 |
| 2,61 | 68 | 70,773603 | 4,078827941 |
| 3,6 | 80 | 76,97328 | 3,7834 |
| 3,52 | 73 | 76,472296 | 4,756569863 |
| 3,94 | 77 | 79,102462 | 2,73047013 |
| 3 | 67 | 73,2159 | 9,277462687 |
Среди 14 измерений найдём абсолютную среднюю ошибку, она составляет 3,13%
Вывод:
В ходе работы научились методу нахождения численных оценок коэффициентов линейного уравнения регрессии и вычисление коэффициента корреляции между переменными х и у = f (х).

