Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра автоматизированных систем управления

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Контрольная работа №2

Вариант 2.2

	Выполнил: Студент гр. з-432П8-5 (номер группы) _______________ / П.С. Нагибин/ (подпись) И. О. Фамилия «02» октября 2022 г. (дата) 111674, Российская Федерация, г. Москва, ул. Льва Яшина, д. 9, кв. 161 (почтовый адрес)
	Проверил: Доцент, кандидат физико-математических наук (должность, ученая степень, звание) ______________ / О.В. Васильева/ (подпись) И. О. Фамилия «____»_______________2022 г. (дата)

Томск 2022

Задание № 1:
1(РД2.РП). Запишите общее уравнение прямой, проходящей через точку

M₀(2,−3) параллельно вектору AB, если A(4, 5), B(3,−7).
Решение:
Точка M₀(2,−3) 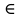прямой L, возьмем произвольную точку M₁(x_M1,y_M1) 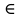прямой L. Очевидно, что векторы M₀M₁ и AB коллиниарны, следовательно их координаты должны быть пропорциональны, запишем уравнение прямой в каноническом виде:
, где:
m – координаты вектора AB по оси х.

n – координаты вектора AB по оси y.
Вычислим координаты вектора AB по его точкам, для этого из координаты конца точки B вычтем соответствующие координаты начала точки A.
AB (3 – 4, –7 – 5) = (–1, –12)
Подставим координаты точки M₀ и вектора AB в уравнение канонического вида:

---

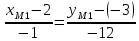
Преобразуем уравнение канонического вида к уравнению общего вида:
Ax + By + C = 0



Ответ: .

Задание № 2:
2(А82.Б7). Стороны треугольника ABC заданы уравнениями AB: 4x − y − 7 = 0;

BC: x + 3y − 31 = 0; AC: x + 5y − 7 = 0. Запишите общее уравнение высоты AH.
Решение:
Вектор AH перпендикулярен стороне BC треугольника ABC, а следовательно, является вектором нормали для стороны BC, т. к. сторона ВС треугольника ABC задана уравнением прямой в общем виде, то согласно определению вектора нормали, вектор AH будет иметь координаты AH (1,3).
Вектор AH является направляющим вектором для прямой AH. Точка А (x, y) 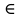прямой AH, для составления уравнения в общем виде прямой AH необходимо определить координаты точки А (x, y) и составить уравнение прямой по точке и вектору нормали.
Точка А (x, y) лежит на пересечении прямых AB и AC, для определения координат точки А (x, y) необходимо решить систему уравнений:

Из уравнения прямой AB выразим у и подставим в уравнение AC.





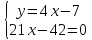
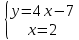
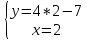
Определили координаты точки А (2, 1).
Составим уравнение в общем виде прямой AH зная координаты точки А (2, 1) и координаты направляющего вектора AH (1,3).
Для этого запишем в каноническом виде уравнение прямой AH:


И запишем уравнение прямой AH в общем виде:

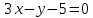
Ответ: 3x-y-5=0.

Задание № 3:
3(432.БЛ). Запишите общее уравнение плоскости, проходящей через точки

M₁(3, 0, 4) и M₂(1, 1, 0) перпендикулярно плоскости 2x + y + 4z − 7 = 0.

---

Решение:
Найдем вектор M₁M₂:
M₁M₂(1-3,1-0,0-4)

M₁M₂(-2,1,-4)
Вектор n(2,1,4) – вектор нормали данной плоскости.

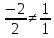
Значит векторы M₁M₂ и n неколлинеарны.

Уравнение искомой плоскости составим по точке M₁(3, 0, 4) и двум неколлинеарным векторам M1M2(-2,1,-4) и n(2,1,4):






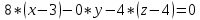
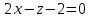
Ответ: 2x-z-2=0.

Задание № 4:
4(С35). Найдите расстояние от точки P(2, 4, 4) до прямой .
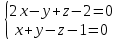Решение:
Потребуется найти направляющий вектор и какую-либо точку, принадлежащую данной прямой.
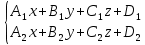, то
направляющий вектор прямой p:

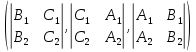
В данном случае p:


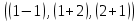
p
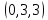
Теперь найдем какую-либо точку М(x,y) 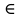данной прямой, пусть z=0, тогда: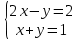





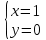
Точка М(1,0,0) 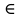данной прямой.

Формула расстояния от точки до прямой в пространстве:


Вычислим вектор PM:
PM(1-2,0-4,0-4)
PM(-1,-4,-4)
Вычислим векторное произведение PM*p:

i((-4)*3 - 3*(-4)) – j((-1)*3 – 0*(-4)) + k((-1)*3 – 0*(-4)) = (0,-3,-3)

---

Ответ: расстояние от точки до прямой равно 1.

Задание № 5:
5(435). Плоскость проходит через прямую , параллельно вектору AB(8, 4, 7). Найдите длину отрезка, отсекаемого этой плоскостью от оси ординат.
Решение:
По общему уравнению прямой найдём её направляющий вектор l, для этого перепишем уравнение прямой записав все коэффициенты:

l = 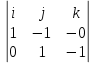= i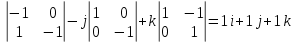
Видим, что l(1,1,1).
Получим координаты точки прямой M₀, полагая y = 0 в общем уравнении прямой:


Видим, что M₀(-1,0,-2).
Плоскость P параллельна направляющему вектору l прямой и вектору AB,

поэтому её уравнение записываем по двум направляющим векторам и точке M₀:






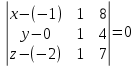
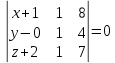
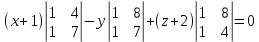
Перепишем уравнение плоскости в отрезках:



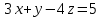
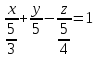
Следовательно длина отрезка, отсекаемого этой плоскостью от оси ординат равна 5.
Ответ: длина отрезка, отсекаемого этой плоскостью от оси ординат равна 5.

Задание № 6:
6(СП5). Две прямые, пересекающиеся в точке P(0, 0, z₀), z₀ > 0 параллельны

плоскости 2x + y + 2z + 6 = 0 и отстоят от неё на расстоянии 4. Одна из прямых

пересекает ось абсцисс, а вторая — ось ординат. Найдите тангенс острого угла

между ними.
Решение:
Расстояние от точи P(0, 0, z₀) до плоскости можно найти по формуле:

---

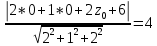
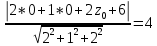
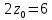
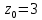
Видим, что P(0,0,3).
Обозначим точку пересечения оси абсцисс M(x,0,0) и точку пересечения оси ординат N(0,y,0), тогда вектор PM(x,0,-3), а вектор PN(0,y,-3)
Из уравнения плоскости 2x + y + 2z + 6 = 0 возьмем вектор нормали n(2,1,2).
Т.к. вектор PM(x,0,-3) перпендикулярен вектору n(2,1,2), то скалярное произведение PM*n = 0, следовательно 2x – 6 = 0, x = 2.
Т.к. вектор PN(0,y,-3) перпендикулярен вектору n(2,1,2), то скалярное произведение PN*n = 0, следовательно y – 6 = 0, y = 6.
Видим, что PM(2,0,-3) и PN(0,6,-3)
Косинус угла между векторами можно найти по формуле:





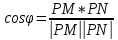
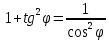
Следовательно, 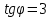, т.к. угол острый, то 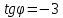не подходит.
Ответ:

Задание № 7:
7(942). Найдите радиус окружности с центром в точке M(2, 4), если известно,

что прямая 3x + 4y + 8 = 0 касается этой окружности
Решение:
Расстояние от точки до касательной есть радиус окружности, который можно найти по формуле расстояние от точки до прямой:


Ответ: радиус окружности равен 6.

Задание № 8:
8. Дана кривая 25x² + 16y² - 150x - 32y - 159 = 0.
8.1. Докажите, что эта кривая — эллипс.
8.2(922.РП). Найдите координаты центра его симметрии.

---

Смотрите также файлы

• Протокол Зав кафедрой Маркелов С. Н. Фио подпись гбпоу мгкэит.docx

• нері рге жзсін.docx

• Инструкция по созданию корректировок приходов в магазинах Магнит Для проведения полного недовоза по алкогольной ро выполните следующие действия.pdf

• Практических заданий по дисциплине основы самообразования.docx

• Практическое задание 1 По части 1 курса вам будет предложено четыре варианта заданий, из которых вы должны выбрать один, в зависимости от буквы, на которую начинается ваша фамилия. Таблица выбора.docx