8.3(С12.РП). Найдите его большую и малую полуоси.
8.4(932). Запишите уравнение фокальной оси.
8.5. Постройте данную кривую.
Решение:
8.1. Докажите, что эта кривая — эллипс.



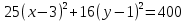
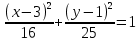– уравнение эллипса.
8.2(922.РП). Найдите координаты центра его симметрии.
Центр эллипса находится в точке (3,1)
8.3(С12.РП). Найдите его большую и малую полуоси.
Большая полуось b = 5, малая полуось a = 4.


8.4(932). Запишите уравнение фокальной оси.

8.5. Постройте данную кривую.


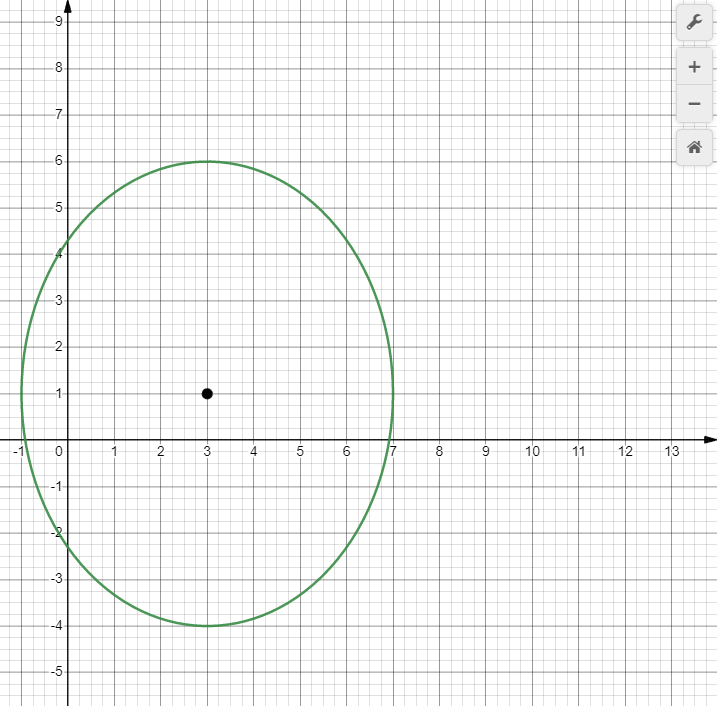
Задание № 9:
9. Дана кривая y2 - 2y + 4x + 9 = 0.
9.1. Докажите, что данная кривая — парабола.
9.2(7Т2.РП). Найдите координаты её вершины.
9.3(342). Найдите значение её параметра p.
9.4(312). Запишите уравнение её оси симметрии.
9.5. Постройте данную параболу.
Решение:
9.1. Докажите, что данная кривая — парабола.




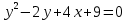
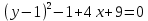
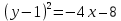
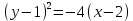
Предположим, что y₁= y – 1, а x­₁ = x – 2, тогда уравнение примет вид:
– уравнение параболы.


9.2(7Т2.РП). Найдите координаты её вершины.
Координаты вершины (-2,1).


9.3(342). Найдите значение её параметра p.
p = -2.


9.4(312). Запишите уравнение её оси симметрии.
y = 1.

9.5. Постройте данную параболу.


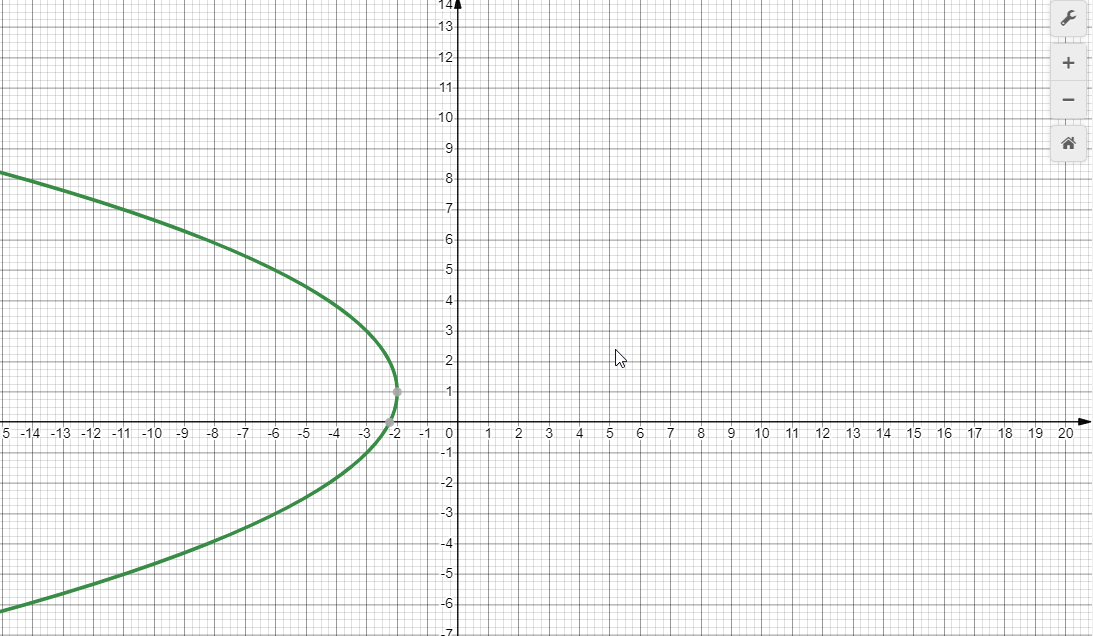
Задание № 10:
10. Дана кривая x² − 7y² − 6xy + 2x + 26y + 57 = 0.

10.1. Докажите, что эта кривая — гипербола.

10.2(9С2.Б7). Найдите координаты её центра симметрии.

10.3(382.РП). Найдите действительную и мнимую полуоси.

---

10.4(АМ2.БЛ). Запишите уравнение фокальной оси.

10.5. Постройте данную гиперболу
Решение:
10.1. Докажите, что эта кривая — гипербола.
Приведем квадратичную форму 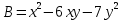к главным осям. Матрица этой квадратичной формы: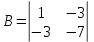

Находим собственные числа и собственные векторы этой матрицы:

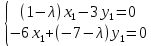
Характеристическое уравнение:




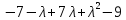
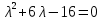
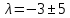
Корни .
Исходное уравнение определяет гиперболу (λ₁ > 0; λ₂ < 0).
Вид квадратичной формы:

10.2(9С2.Б7). Найдите координаты её центра симметрии.
Приведем уравнение к каноническому виду, для этого найдем главные оси квадратичной формы, то есть собственные векторы матрицы B.
Для собственного вектора числа , составляем систему:



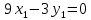
Собственный вектор, отвечающий числу :
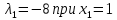x₁(1,3)
Длина вектора x₁:

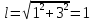
За единичный собственный вектор принимает вектор:

Или:

---

Координаты второго собственного, соответствующего второму собственному числу 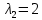найдем из системы:


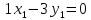
x₂(3,-1) = 0


Имеем новый ортонормированный базис: (l₁,j₁).
Перейдем к новому базису:

Или:

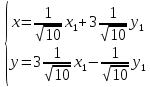
Подставляем выражения x и y в исходное уравнение x² − 7y² − 6xy + 2x + 26y + 57 = 0:


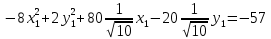
Выделяем полные квадраты:
Для x_1:

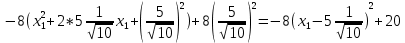
Для y_1:

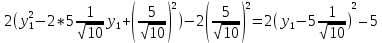
Итоговое выражение примет вид:

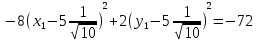
Разделим выражение на -72 и получим канонический вид уравнения гиперболы:

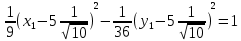
Выполним параллельный перенос системы координат в новое начало O_1:


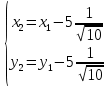
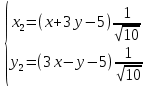
В новой системе координат (O₁,l₁,j₁) выражение примет вид:

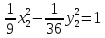
В старой системе координат ось x₂ задается уравнением:


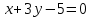
В старой системе координат ось y₂ задается уравнением:


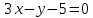
Начало новой системы координат является пересечением координатных осей, для определения новой точки начала координат решим систему уравнений:

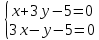
Откуда точка O

---

₁(2,1) – является центром симметрии гиперболы.
10.3(382.РП). Найдите действительную и мнимую полуоси.
Из канонического уравнения гиперболы:

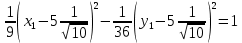
Очевидно, что действительная полуось а = 3, а мнимая b = 6.
10.4(АМ2.БЛ). Запишите уравнение фокальной оси.
Фокальной осью является прямая у₂ = 0, 3х – у – 5 = 0.
10.5. Постройте данную гиперболу

---

Смотрите также файлы

• Протокол Зав кафедрой Маркелов С. Н. Фио подпись гбпоу мгкэит.docx

• нері рге жзсін.docx

• Инструкция по созданию корректировок приходов в магазинах Магнит Для проведения полного недовоза по алкогольной ро выполните следующие действия.pdf

• Практических заданий по дисциплине основы самообразования.docx

• Практическое задание 1 По части 1 курса вам будет предложено четыре варианта заданий, из которых вы должны выбрать один, в зависимости от буквы, на которую начинается ваша фамилия. Таблица выбора.docx