ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 4
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Актуальные методы решений диофантовых уравнений
Оглавление
| Введение | 3 |
| Глава 1. Исторические аспекты решения диофантовых уравнений | 4 |
| Глава 2. Диофантовы уравнения и их свойства | 5 |
| Глава 3. Актуальные методы решения диофантовых уравнений первой степени | 6 |
| Заключение | 9 |
| Список литературы | 10 |
| Приложения | 11 |
| | |
| | |
Введение
Впервые о Диофанте и его уравнениях мы услышали еще в 4 классе. Вполне естественно, что в этом возрасте интереса к столь трудным и таким непонятным на тот момент объектам математики я не проявила. Намного позднее с диофантовыми уравнениями мне пришлось столкнуться, принимая участие во всероссийской олимпиаде по математике Эйдос.
Актуальность исследования заключается в том, что подход Диофанта к решению данных уравнений особенно интересен. Способы решения его уравнений довольно просты, несмотря на то, что уравнения могут состоять из двух, трёх и более переменных.
Проблема заключается в том, что в связи с отсутствием в школьной программе вопросов с решением диофантовых уравнений, школьники не могут решать материал итоговой государственной аттестации.
Гипотеза исследования: математическая подготовка школьников будет проходить успешнее, если раскрыть актуальные методы решения диофантовых уравнений.
Предмет исследования: диофантовы уравнения первой степени.
Цель работы: выявить актуальные методы решения диофантовых уравнений первой степени и выбрать наиболее рациональные методы их решения.
Задачи:
-
Рассмотреть историю развития диофантовых уравнений 1 степени. -
Дать определение диофантовым уравнениям и рассмотреть их свойства. -
Рассмотреть и сравнить актуальные методы решения диофантовых уравнений 1 степени, а также установить межпредметные связи.
Глава 1. Исторические аспекты решения диофантовых уравнений
О подробностях жизни одного из древнегреческих математиков Диофанта Александрийского практически ничего неизвестно. Однако его труды имели большое значение для алгебры и теории чисел. В его книге «Арифметика» впервые встречаются уравнения, решения которых нужно найти на множестве целых чисел. Такие уравнения впоследствии получили название«диофантовых уравнений».
Наиболее загадочным представляется творчество Диофанта. Основное произведение Диофанта – «Арифметика» в тринадцати книгах. К всеобщему сожалению, до наших дней сохранились только первые шесть. «Арифметика» Диофанта представлена как ряд задач. В основном «Арифметика» посвящена решению уравнений. В первой из сохранившихся книг обсуждаются линейные уравнения; в остальных пяти рассматриваются различные виды квадратных уравнений, часто для нескольких неизвестных, а также некоторые специальные кубические уравнения. Характерная особенность состоит в том, что ответы всегда являются целыми или рациональными числами.
Задачи диофантовой «Арифметики» сводятся к уравнениям или к системам уравнений с целыми коэффициентами. Эти системы неопределенные, т.е. число уравнений в них меньше числа неизвестных переменных. Кроме того, решения требуется найти только целые, часто натуральные.
Конкретные задачи такого рода были решены еще в Древнем Вавилоне около 4 тысяч лет тому назад. Древнегреческий мыслитель Диофант, который жил около 2 тысяч лет тому назад, в своей книге «Арифметика» решил большое число таких и более сложных уравнений в целых числах и в сущности описал общие методы их решения.
Глава 2. Диофантовы уравнения и их свойства
Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях больше числа уравнений.
Диофантовы уравнения обладают рядом свойств. Количество решений уравнения зависит от коэффициентов aи b. Приведем формулировки теорем о числе решений, на основании которых может быть составлен алгоритм решения неопределенных уравнений первой степени от двух переменных в целых числах.
Теорема 1. Если в уравнении aх + by = 1, (a,b) = 1, то уравнение имеет, по крайней мере, одно решение.
Теорема 2. Если в уравнении aх + by = с, (a, b) = d> 1 и c не делится на d, то уравнение целых решений не имеет.
Теорема 3. Если в уравнении aх + by = с, (a, b) = d> 1 иc
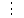d, то оно равносильно уравнению a1x + b1y = c1, в котором (a1, b1) = 1. Теорема 4. Если в уравненииax + by = c , (a, b) = 1, то все целые решения этого уравнения заключены в формулах: х=х0с+bt , y=y0с –at, где х0, у0 – целое решение уравнения aх+by=1, t– любое целое число.
Следует отметить, что каждая конкретная задача в целых числах может решаться с помощью разных методов.
Глава 3. Актуальные методы решений диофантовых уравнений 1 степени
Методы решения неопределенных уравнений составляют основной вклад Диофанта в математику. Уравнения, решаемые в целых числах, всегда притягивали интерес математиков и по праву считаются самым красивым разделом математики.
Долгое время ученые пытались найти общий способ решения диофантовых уравнений, но все тщетно. Известная «Десятая проблема Гильберта» – одна из 23 задач, которые Давид Гильберт предложил 8 августа 1900 года на II Международном конгрессе математиков. Она состоит в нахождении универсального метода целочисленного решения произвольного алгебраического диофантова уравнения. Доказательство алгоритмической неразрешимости этой задачи заняло около двадцати лет и в 1970 г. Ленинградский математик Матиясевич доказал, что такого общего способа быть не может. Методы решения неопределенных уравнений составляют основной вклад Диофанта в математику. Уравнения, решаемые в целых числах, всегда притягивали интерес математиков и по праву считаются самым красивым разделом математики.
1 способ: Метод перебора – применяется для решения простейших задач. Заключается в выражении одной переменной через другую и переборе возможных вариантов.
Задача 1.В парке прогуливаются люди с собаками. Вместе у них 20 ног и лап. Сколько людей и сколько собак в парке?
Решение. Составляется уравнение с двумя неизвестными переменными, в котором х – число собак, у – число людей:4х + 2у = 20, или 2х + у = 10.Выразим у через х:у = 10 – 2х.
Далее воспользуемся методом перебора:
| Х | 1 | 2 | 3 | 4 |
| У | 8 | 6 | 4 | 2 |
Значит, задача имеет четыре решения.
Ответ: (1; 8), (2; 6), (3; 4), (4; 2).
2 способ: Алгоритм Евклида. Этот метод заключается в уменьшении коэффициентов уравнения с помощью деления на наибольший общий делитель. Когда будут получены взаимно простые коэффициенты, находим частное большего и меньшего коэффициентов. Данная операция может повторятся многократно, до тех пор, пока в остатке не будет получена единица. Из последнего равенства выражаем единицу и возвращаемся к изначальному уравнению. С его помощью можно решить уравнение в целых числах 407х – 2816y = 33. Полное решение см. Приложение1
3 способ: Метод рассеивания.
В Индии, где неопределенные уравнения решались в связи с астрономическими запросами и календарными расчетами, ставился вопрос о нахождении именно целочисленных решений неопределенных уравнений. Намеки на общее решение диофантовых уравнений первой степени, т.е. вида
aх +by = с, встречаются впервые в трудах индийского астронома Ариабхатты. Общий метод для решения в целых числах неопределенных (диофантовых) уравнений первой степени с целыми коэффициентами был назван в Индии методом рассеивания (размельчения).
Данный способ еще называют – «методом спуска» и заключается в выражении одной переменной через другую, выделении целой части и вводе новой переменной, получаем новое уравнение, но с меньшими коэффициентами, до тех пор, пока не исчезнут дроби. Затем «поднимаемся вверх» и находим сразу общее решение. При решении задачи 3 новые переменные вводили 3 раза. Полное решение смотрите в приложении 2.
Задача 3. Для газификации жилого дома требуется проложить газопровод длиной 39м. Имеются трубы 5 м и 8 м длиной. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода?
4 способ: Графический способ. Уравнение можно представить в виде линейной функции, выразив y. По ней чертится график и определяются точки, обе координаты которых являются положительными целыми числами.
Задача 4. Надо разлить 17 л жидкости в бутыли емкостью в 5 л и 7 л так, чтобы все использованные бутыли были полными. Сколько потребуется бутылей той и другой емкости?
У
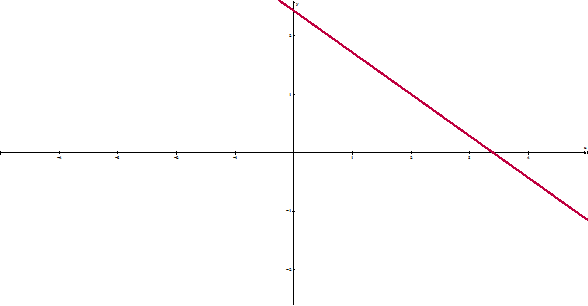равнение 5x+7y=17 можно решить графическим методом, изобразив прямую 5x+7y= 17, и определив на этой прямой точки, обе координаты которых будут в данном случае натуральными числами. Рис. 1Целые решения: (2;1),(9; –4), (16; –9),(–5;6),(–12;11).
Задача 5. Решить уравнение 5х–8у=1 геометрически при помощи окружности.
Отложим на окружности последовательно друг за другом равные дуги, составляющие
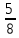-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов. На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 
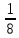-ю часть окружности, так что х
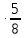= у + 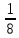. Полное решение смотрите в приложении 3.Заключение
В ходе исследования реализовали все поставленные задачи. Показали исторический аспект поиска решения диофантовых уравнений с древних времен до нашего времени. Рассмотрели ряд теорем, описывающих свойства диофантовых уравнений.
Уравнения первой степени, как мы увидели, решаются довольно просто. Из рассмотренных в ходе исследования методов, метод рассеивания оказался наиболее рациональным, он дает сразу общее решение, не сложный для понимания, не энергозатратный.
Теория решения диофантовых уравнений является классическим разделом элементарной математики. В ней не приходится писать сложные и громоздкие формулы, необходимо проводить лишь аккуратные рассуждения с использованием определенных понятий теории чисел и связанные в стройную логическую конструкцию.
Эту чисто абстрактную теорию можно использовать для построения алгоритмов, которые нужны для криптографии, чтобы зашифровывать и
