ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
безопасно передавать секретные сообщения, а также снимать и класть деньги в банкоматах и т. п. Теория эта оказалась востребована на практике. В России есть целая Академия криптографии и научно-исследовательские организации, которые используют такие разработки.
Мы рассматривали только неопределенные уравнения первой степени. С уравнениями второй степени сложнее. Уравнениями третьей и больше степеней занимаются великие математики, потому что их решения слишком сложны и громоздки. В ближайшее время, планируем рассмотреть уравнения 2 степени.
Литература
ПРИЛОЖЕНИЕ 1
Способ 2. Алгоритм Евклида.
Решить уравнение в целых числах 407х – 2816y = 33.
Воспользуемся составленным алгоритмом.
2816 = 407·6 + 374;
407 = 374·1 + 33;
374 = 33· 11 + 11;
33 = 11·3
Следовательно (407,2816) = 11, причем 33 делится на 11
256 = 37·6 + 34;
37 = 34·1 + 3;
34 = 3·11 + 1
Выразим 1 из последнего равенства, затем последовательно поднимаясь по равенствам будем выражать 3; 34 и полученные выражения подставим в выражение для 1.
1 = 34 – 3·11 = 34 – (37 – 34·1) ·11 = 34·12 – 37·11 = (256 – 37·6) ·12 – 37· 11 = – 83·37 – 256·(–12)
Таким образом, 37·(–83) – 256·(–12) = 1, следовательно, пара чисел
х0 = – 83 и у0 = – 12 есть решение уравнения 37х – 256y = 3.
y = – 12c–at =– 12 3– 37t = – 36 – 37t
3– 37t = – 36 – 37t
где t - любое целое число.
ПРИЛОЖЕНИЕ 2
Способ 3.Метод рассеивания.
Задача 2. Для газификации жилого дома требуется проложить газопровод длиной 39 м. Имеются трубы 5 м и 8 м длиной. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода?
Решить способом измельчения в целых числах уравнение 5x + 8y = 39.
Решение:
1. Выберем неизвестное, имеющее наименьший коэффициент, и выразим его через другое неизвестное: x = (39 – 8y):5.
Выделим целую часть: x = 7 –y + (4 – 3y):5.
Все число будет целым, если целым окажется значение (4 – 3y):5.
Это возможно тогда, когда число (4 – 3y) без остатка делится на 5. Вводя дополнительную целочисленную переменную z, последнее уравнение запишем в виде: 4 –3 y = 5z.
Мы пришли к уравнению такого же типа, как и исходное уравнение, но уже с меньшими коэффициентами. Решать его уже нужно относительно переменных y и z.
2. y= (4 – 5z): 3 = 1 – z + (1 – 2z):3
Аналогично рассуждая, запишем (1 – 2z) через новую целочисленную переменную и: 1–2z=3u
3. z = (1–3u):2=(1– u):2 – u;
1– u=2v
4. u=1 –2v - дробей больше нет, спуск закончен.
5. Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x.
z =(1– u):2 –u=(1–1+2v):2–1+2v= 3v–1,
z = 3v– 1.
y = (4–5z):3 = (4 – 5(3v – 1)):3=3– 5v,
y = 3 – 5v.
x = (39 – 8y) : 5 = (39 – 8(3 – 5v)) : 5 = 3 + 8v,
x=3+8v.
6. Формулы x=3+8v, y=3– 5v представляют общее решение исходного уравнения в целых числах.
7. Если необходимо получить только натуральные числа, то среди
всех целых решений нужно выбрать такие, для которых x>0, y>0, то есть 3+8v>0,3 – 5v>0.
Совместно эти неравенства могут выполняться лишь при v=0. В этом случае x=3, y=3
ПРИЛОЖЕНИЕ 3
Задача 5. Решим уравнение 5х–8у=1 геометрически.
Решение. Запишем частное решение уравнения (1).Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие
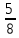 -ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов. На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли
-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов. На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 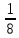 -ю часть окружности, так что х
-ю часть окружности, так что х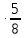 = у +
= у + 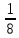 .Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
.Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
Частное решение уравнения (1): Хо = 19 5=95; уо =19
5=95; уо =19 3=57.
3=57.
Общее решение уравнения (1):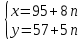 n
n 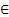 Z. Рис.2 …..
Z. Рис.2 …..
Мы рассматривали только неопределенные уравнения первой степени. С уравнениями второй степени сложнее. Уравнениями третьей и больше степеней занимаются великие математики, потому что их решения слишком сложны и громоздки. В ближайшее время, планируем рассмотреть уравнения 2 степени.
Литература
-
Бардушкин В.В., Кожухов И.Б., Прокофьев А.А., Фадеичева Т.П. Основы теории делимости чисел. Решение уравнений в целых числах. Факультативный курс. – М.: МГИЭТ(ТУ), 2003. – 224 с. -
Башмакова И. Г. Диофант и диофантовы уравнения.– М.: изд. «Наука», 1972. –68с. -
Бухштаб А. А., Теория чисел. – М.: Просвещение, 1966. –385 с. -
Деев М.Е. Методы решения олимпиадных задач на доказательство. // Информация и образование: границы коммуникаций (INFO 13): Сборник научных трудов № 5(13) / под ред. Темербековой А.А., Гальцевой Н.П. – Горно-Алтайск: РИО ГАГУ, 2013. – 462с. -
Никифоровский В. А. В мире уравнений.–М.: изд. «Наука» 1987.– 176с. -
Серпинский В. О решении уравнений в целых числах. – М.: Физматлит, 1961.– 88 с. -
Шпилекова Л.Н. Методика решения диофантовых уравнений при подготовке школьников к олимпиадам. // Информация и образование: границы коммуникаций INFO 16: Сборник научных трудов № 8(16) / под ред. Темербековой А.А., Альковой Л.А. – Горно-Алтайск: РИО ГАГУ, 2016. – 258с.
ПРИЛОЖЕНИЕ 1
Способ 2. Алгоритм Евклида.
Решить уравнение в целых числах 407х – 2816y = 33.
Воспользуемся составленным алгоритмом.
-
Найдем наибольший общий делитель чисел 407 и 2816:
2816 = 407·6 + 374;
407 = 374·1 + 33;
374 = 33· 11 + 11;
33 = 11·3
Следовательно (407,2816) = 11, причем 33 делится на 11
-
Разделим обе части первоначального уравнения на 11, получим уравнение 37х – 256y = 3, причем (37, 256) = 1 -
Найдем линейное представление числа 1 через числа 37 и 256.
256 = 37·6 + 34;
37 = 34·1 + 3;
34 = 3·11 + 1
Выразим 1 из последнего равенства, затем последовательно поднимаясь по равенствам будем выражать 3; 34 и полученные выражения подставим в выражение для 1.
1 = 34 – 3·11 = 34 – (37 – 34·1) ·11 = 34·12 – 37·11 = (256 – 37·6) ·12 – 37· 11 = – 83·37 – 256·(–12)
Таким образом, 37·(–83) – 256·(–12) = 1, следовательно, пара чисел
х0 = – 83 и у0 = – 12 есть решение уравнения 37х – 256y = 3.
-
Запишем общую формулу решений первоначального уравнения
x = – 83c + bt= – 83 3 – 256t = – 249 – 256t
3 – 256t = – 249 – 256t
y = – 12c–at =– 12
 3– 37t = – 36 – 37t
3– 37t = – 36 – 37tгде t - любое целое число.
ПРИЛОЖЕНИЕ 2
Способ 3.Метод рассеивания.
Задача 2. Для газификации жилого дома требуется проложить газопровод длиной 39 м. Имеются трубы 5 м и 8 м длиной. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода?
Решить способом измельчения в целых числах уравнение 5x + 8y = 39.
Решение:
1. Выберем неизвестное, имеющее наименьший коэффициент, и выразим его через другое неизвестное: x = (39 – 8y):5.
Выделим целую часть: x = 7 –y + (4 – 3y):5.
Все число будет целым, если целым окажется значение (4 – 3y):5.
Это возможно тогда, когда число (4 – 3y) без остатка делится на 5. Вводя дополнительную целочисленную переменную z, последнее уравнение запишем в виде: 4 –3 y = 5z.
Мы пришли к уравнению такого же типа, как и исходное уравнение, но уже с меньшими коэффициентами. Решать его уже нужно относительно переменных y и z.
2. y= (4 – 5z): 3 = 1 – z + (1 – 2z):3
Аналогично рассуждая, запишем (1 – 2z) через новую целочисленную переменную и: 1–2z=3u
3. z = (1–3u):2=(1– u):2 – u;
1– u=2v
4. u=1 –2v - дробей больше нет, спуск закончен.
5. Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x.
z =(1– u):2 –u=(1–1+2v):2–1+2v= 3v–1,
z = 3v– 1.
y = (4–5z):3 = (4 – 5(3v – 1)):3=3– 5v,
y = 3 – 5v.
x = (39 – 8y) : 5 = (39 – 8(3 – 5v)) : 5 = 3 + 8v,
x=3+8v.
6. Формулы x=3+8v, y=3– 5v представляют общее решение исходного уравнения в целых числах.
7. Если необходимо получить только натуральные числа, то среди
всех целых решений нужно выбрать такие, для которых x>0, y>0, то есть 3+8v>0,3 – 5v>0.
Совместно эти неравенства могут выполняться лишь при v=0. В этом случае x=3, y=3
ПРИЛОЖЕНИЕ 3
Задача 5. Решим уравнение 5х–8у=1 геометрически.
Решение. Запишем частное решение уравнения (1).Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие
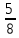 -ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов. На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли
-ю часть полной окружности. За 8 шагов получим все вершины правильного вписанного в окружность 8-угольника. При этом сделаем 5 полных оборотов. На 5-ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 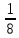 -ю часть окружности, так что х
-ю часть окружности, так что х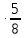 = у +
= у + 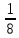 .Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
.Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.Частное решение уравнения (1): Хо = 19
 5=95; уо =19
5=95; уо =19 3=57.
3=57.Общее решение уравнения (1):
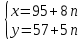 n
n 


