Задание по дисциплине «Высшая математика»

1 курс

Семинар №1

Задача 1. Вычислить пределы данных функций.

а) ; б) ;

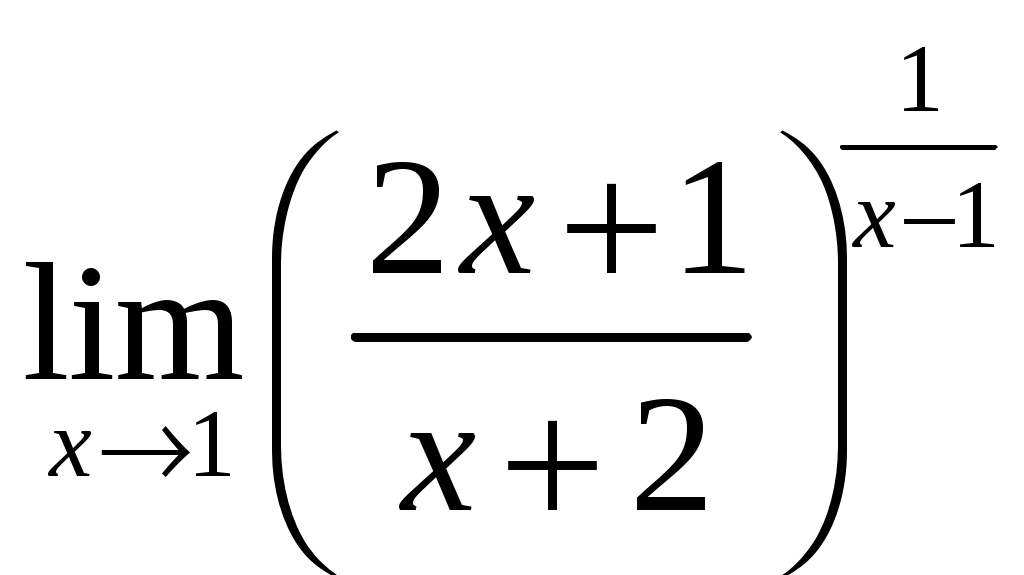в) ; г) .

Решение.

а) .

Под знаком предела есть иррациональность в числителе дроби. Непосредственная подстановка предельного значения аргумента x=8 приводит к неопределенности вида .

Чтобы раскрыть эту неопределенность, достаточно числитель и знаменатель дроби, стоящей под знаком предела, домножить на выражение, сопряженное числителю дроби:



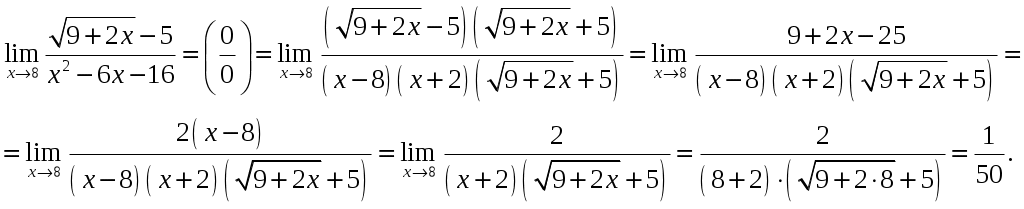
б) .

В этом случае имеем неопределенность вида . Т.к. в числителе и знаменателе стоят многочлены, то для раскрытия неопределенности необходимо числитель и знаменатель разделить на наивысшую степень x из слагаемых многочленов числителя и знаменателя, т.е. на , а затем перейти к пределу:





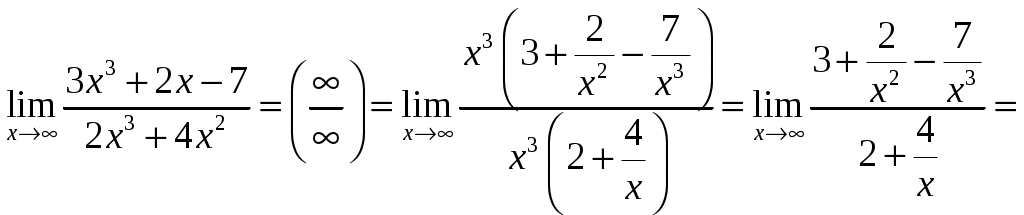
в) .



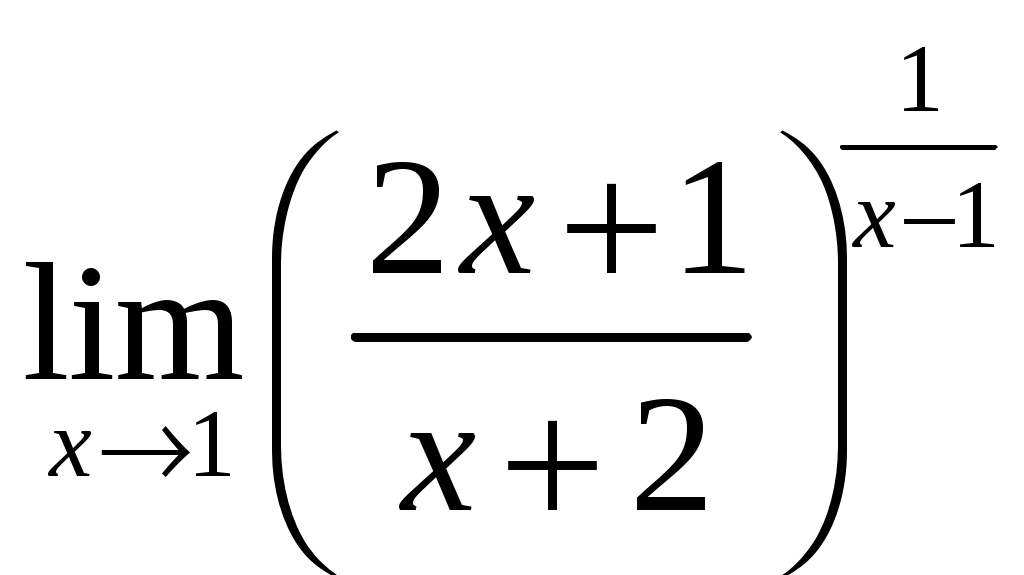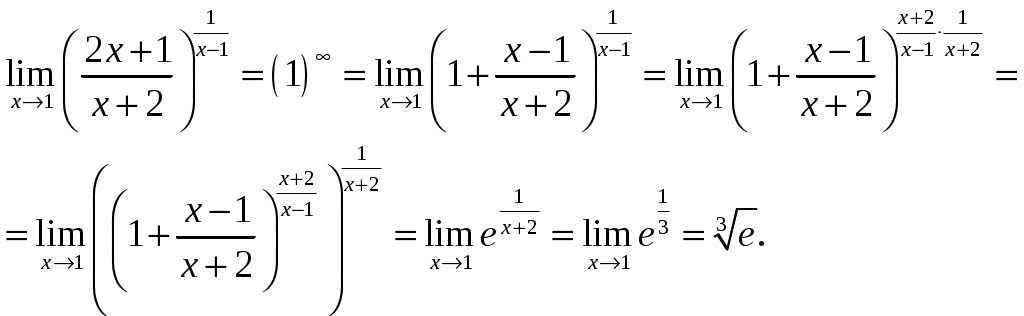
При вычислении этого предела использована обобщенная формула второго замечательного предела и теорема о пределе показательно-степенной функции: , где конечная или бесконечно удаленная точка.

---

г) .

При x=0 числитель и знаменатель дроби равны 0, имеем неопределённость вида . Преобразуем исходную дробь и воспользуемся первым замечательным пределом :



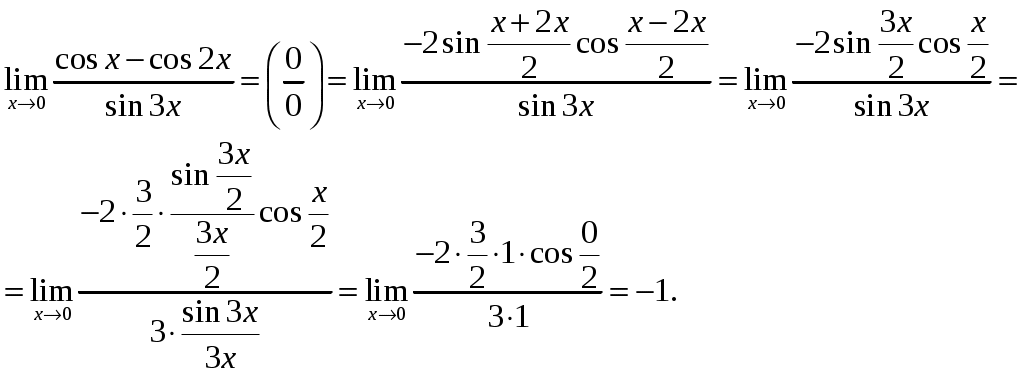
Задача 2. Определить то значение параметра А, для которого функция будет непрерывной (если возможно). Сделать чертеж.



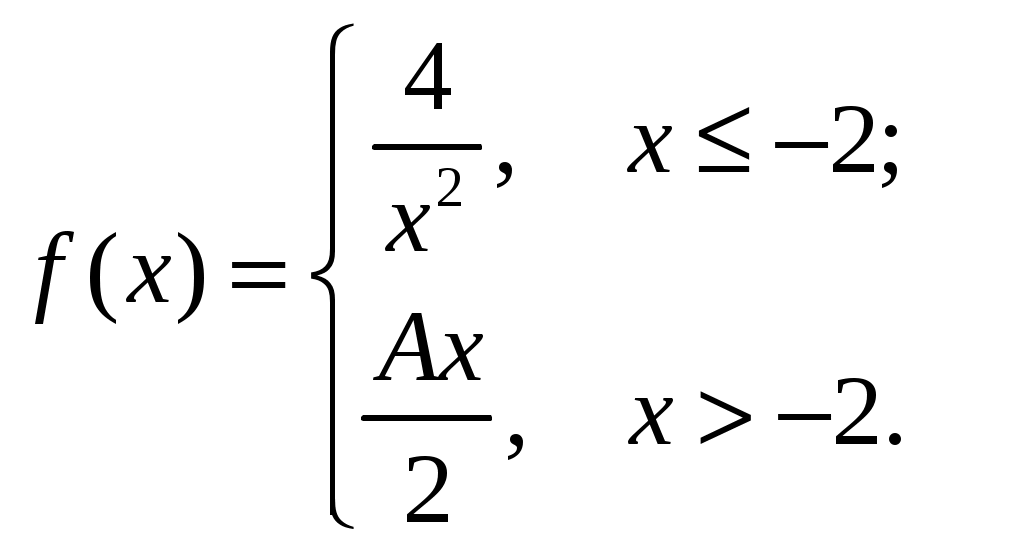
Решение.

Воспользуемся определением непрерывности функции: поскольку ,

и , то из равенства находим .

Перепишем исходную функцию в виде



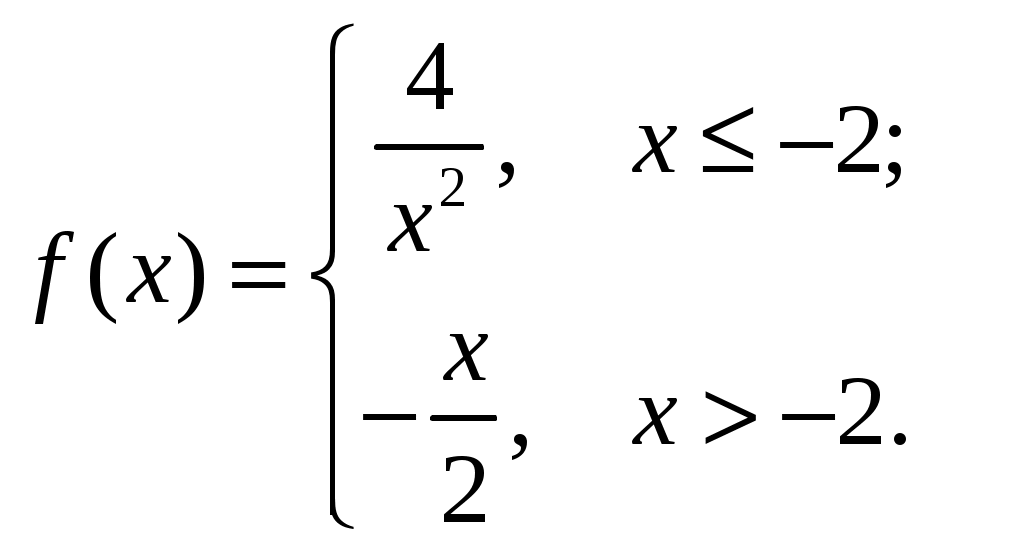
Сделаем чертеж.



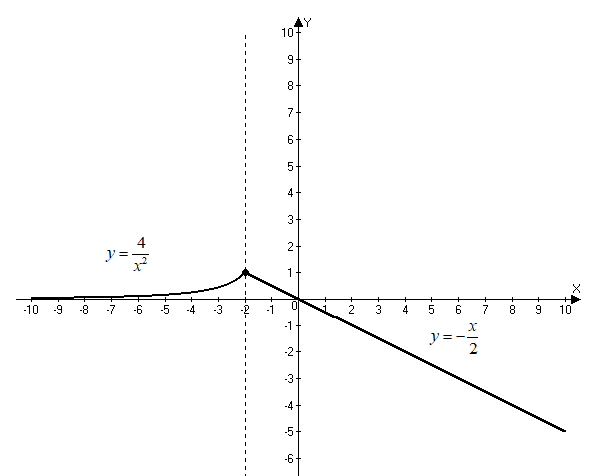
Задача 3. Исследовать функцию методами дифференциального исчисления и построить график.



Решение.

Для полного исследования функции и построения ее графика применяется следующая примерная схема:

1. 
   найти область определения функции;
   
2. 
   исследовать функцию на непрерывность и определить характер точек разрыва;
   
3. 
   исследовать функцию на четность и нечетность, периодичность;
   
4. 
   найти точки пересечения графика функции с осями координат;
   
5. 
   исследовать функцию на монотонность и экстремум;
   
6. 
   найти интервалы выпуклости и вогнутости, точки перегиба;
   
7. 
   найти асимптоты графика функции;
   
8. 
   по полученным данным построить график функции.
   

Применим вышеуказанную схему для исследования данной функции.

---

1. 
   .
   
2. 
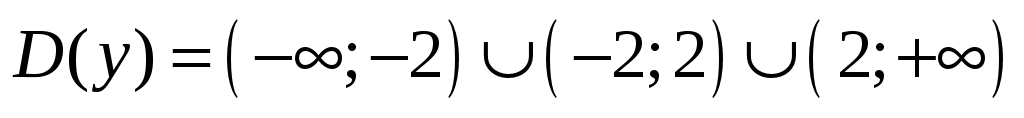   Функция имеет точки разрыва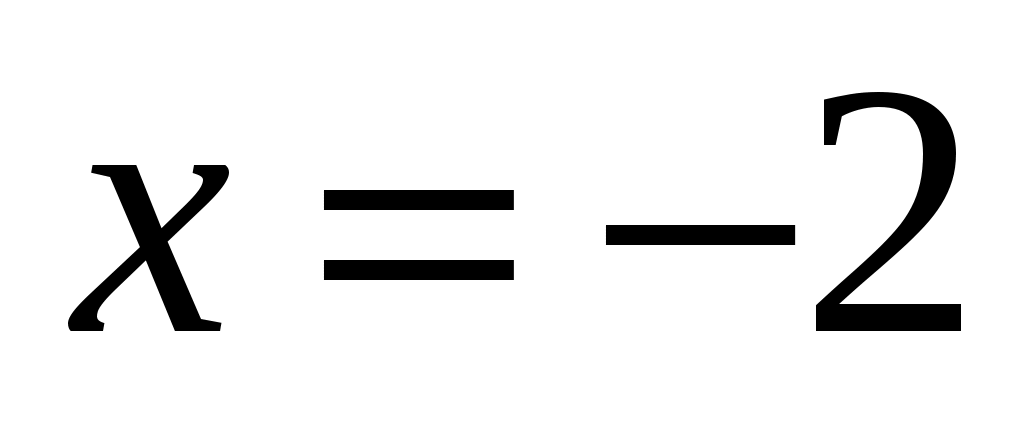 и 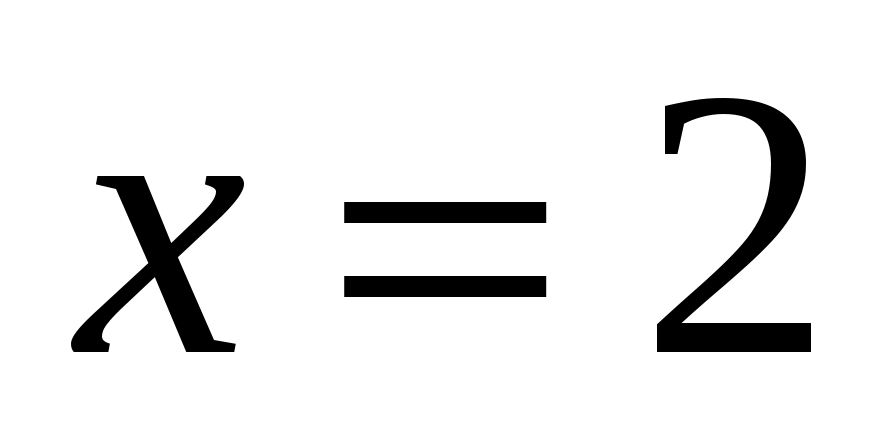и непрерывна для всех 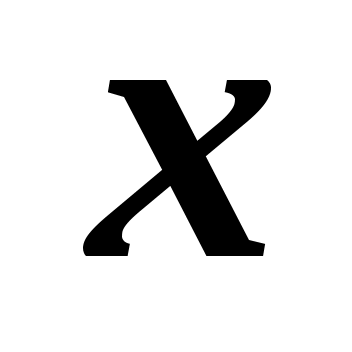из области определения.
   
3. 
   .
   

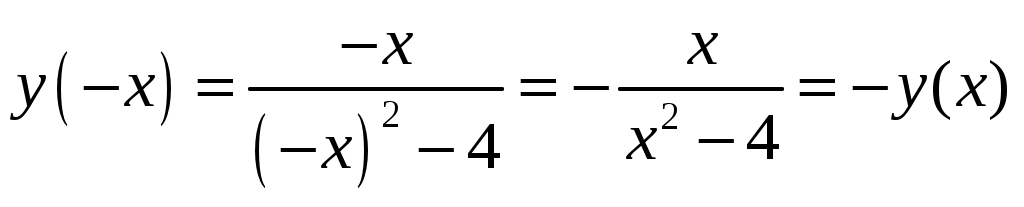Функция является нечетной. Функция не периодическая.

4. 
   С осью Ох: .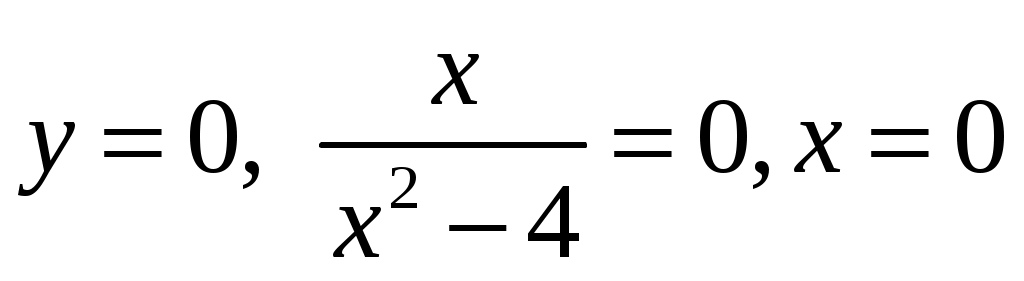
   

Точка (0;0) – точка пересечения графика с осью Ох.

С осью Оу: .

Точка (0;) – точка пересечения графика с осью Оу.

5. 
   Находим производную.
   

при и не существует при x=-2; x=2.

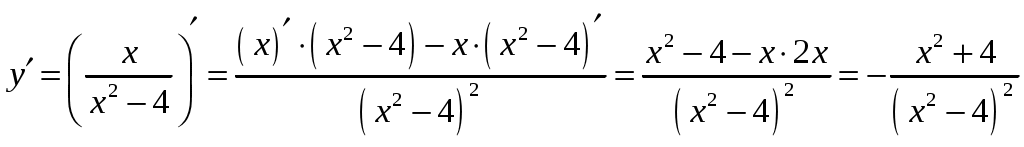
Исследуем знак производной функции на промежутках , т.к. точки x=-2; x=2 точки разрыва

– – –



-2 2

Функция убывает – на всех

6. 
   Находим вторую производную.
   

при

---

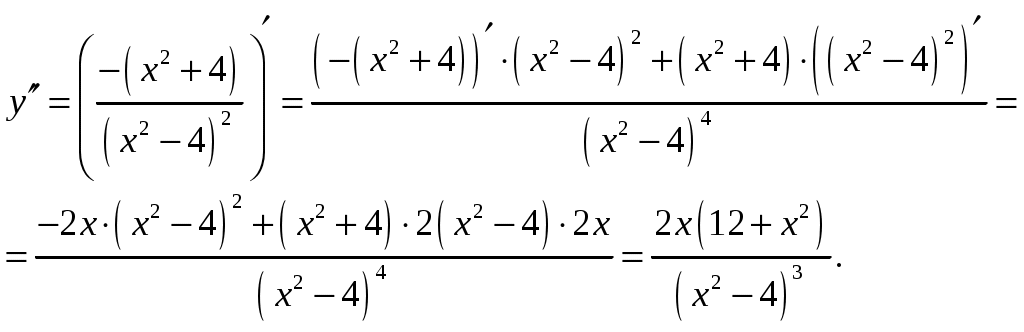
и не существует при x=-2; x=2







– + – +

-2 0 2
при – кривая выпуклая,

при – кривая вогнутая,

при – кривая выпуклая,

при – кривая вогнутая.

Точками перегиба являются точки разрыва и точка х=0.

.

7. 
   Так как точк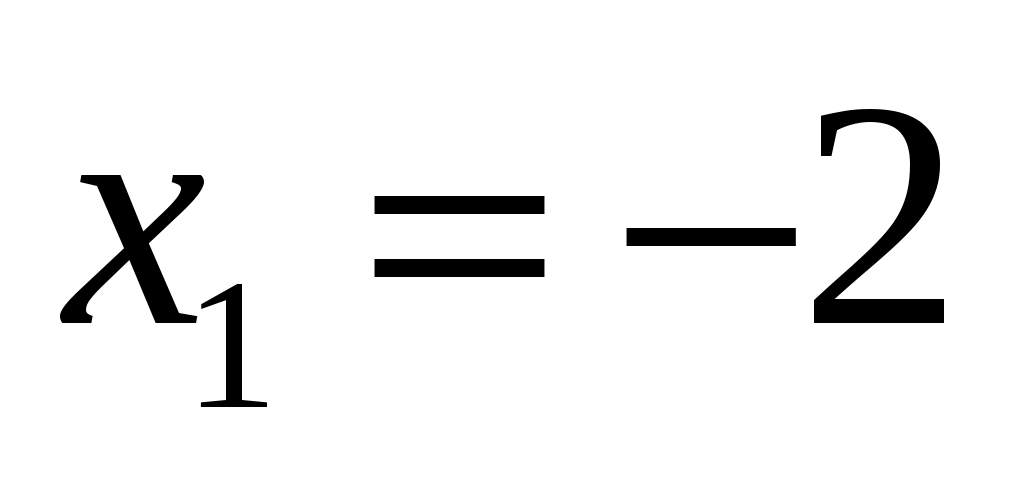и и 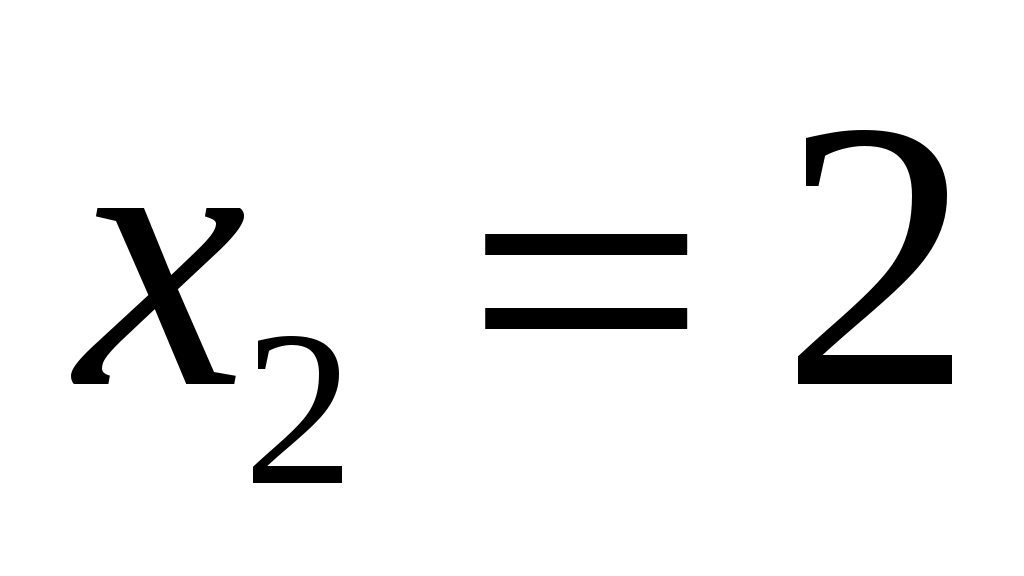- точки разрыва второго рода, то прямые 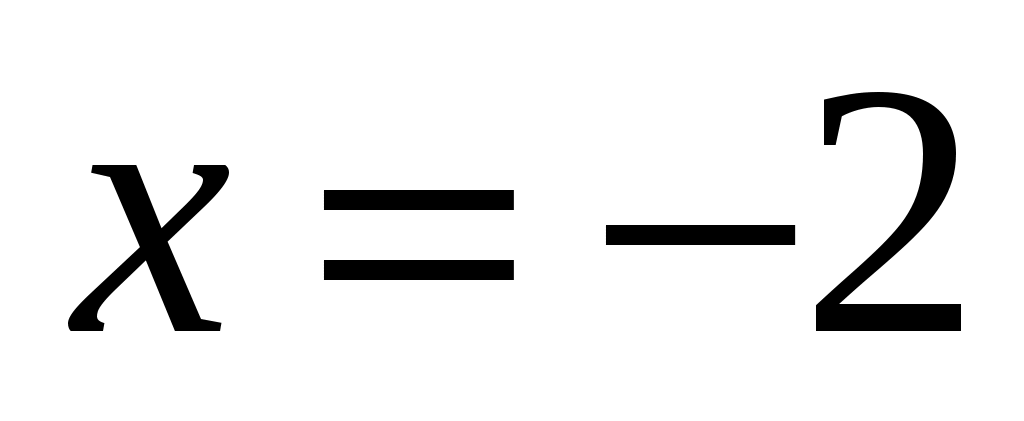и - вертикальные асимптоты.
   

Докажем это, исследуя поведение функции вблизи этих точек.





Найдем наклонные асимптоты

---

Тогда - горизонтальная асимптота

8. 
   По полученным данным строим график функции.
   

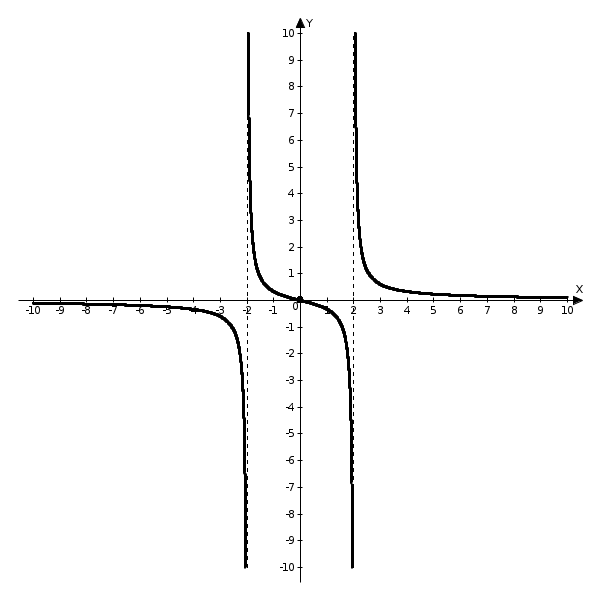
Задача 4. Найти все частные производные второго порядка, включая смешанную производную и дифференциал первого порядка от функции:

.

Решение.

Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными.

Сначала найдём частные производные первого порядка:





Теперь находим производные второго порядка по переменным и :



Находим смешанные производные:





Полный дифференциал функции находим по формуле:



Получаем:



Задача 5. Исследовать на экстремум функцию .

Решение.

Для нахождения точек экстремума, применим необходимое условие локального экстремума дифференцируемой функции:

---

Смотрите также файлы

• Демонстра.docx

• 44. 02. 03 Педагогика дополнительного образования (в области социальнопедагогической деятельности).docx

• Задача Рассчитать сумму налога изаполнить декларацию по усн6%.docx

• Реферат безопасность как основа развития личности ребенка автор реферата Д. А. Аксёнова, студентка v курса группы кдб218.docx

• Фактически первой исторической формы философии.docx