ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 62
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
методе Бонферрони (правильнее говорить о принципе Бонферрони) множественных сравнений, в котором при каждом по парном сравнении задается уровень значимости  , где
, где 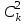 - число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из
- число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из 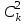 сравнений не превзойдет
сравнений не превзойдет  . Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия.
. Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия.
LSD – критерий и критерий Бонферрони занимают как бы самые крайние позиции в ряду критериев множественных сравнений. Среди остальных критериев множественного сравнения средних можно выделить критерии множественных сравнений Шеффе, Ньюмена-Келса, Тьюки и другие.
В методе множественных сравнений Шеффе для проверки гипотезы равенства средних и
и  используется статистика:
используется статистика:
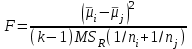 ,
,
где – оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики
– оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики  , где
, где  - критическая точка распределения Фишера уровня
- критическая точка распределения Фишера уровня  (или квантиль уровня
(или квантиль уровня  ) с числом степеней свободы
) с числом степеней свободы  и
и  , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза  .
.
Заметим, что в отличии от LSD критерия, где статистика имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет
имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет
 степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана.
степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана.
В методе множественных сравнений Тьюки (или достоверно значимой разности – HSD) для проверки гипотезы против альтернативы
против альтернативы  используется статистика:
используется статистика:
 ,
,
значения которой сравниваются с критическими точками уровня распределения стьюдентизированного размаха с
распределения стьюдентизированного размаха с 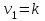 и
и  степенями свободы. Если наблюдаемое значение статистики
степенями свободы. Если наблюдаемое значение статистики  , где
, где 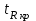 - критическая точка распределения стьюдентизированного размаха уровня
- критическая точка распределения стьюдентизированного размаха уровня  (или квантиль уровня
(или квантиль уровня  ) с числом степеней свободы
) с числом степеней свободы 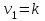 и
и  , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза  .
.
Если объемы выборок различаются сильно, то рекомендуется использовать HSD критерий Тьюки для неравных выборок (критерий Spjovoll-Stoline). Статистика критерия в этом случае имеет вид:
 .
.
Критические точки определяются также, как и для критерия HSD Тьюки.
В критерии Ньюмана-Келса используется та же статистика, что и в критерии Тьюки, однако по другому определяются критические точки. В качестве критических точек критерия Ньюмана-Келса используются критические точки распределения стьюдентизированного размаха с и
и  степенями свободы, где
степенями свободы, где 
- число средних расположенных между и
и 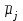 в вариационном ряду выборочных средних, включая
в вариационном ряду выборочных средних, включая  и
и 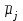 . Например, если сравниваются значения
. Например, если сравниваются значения 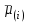 и
и 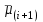 вариационного (упорядоченного) ряда средних, то
вариационного (упорядоченного) ряда средних, то  , если сравниваются значения
, если сравниваются значения 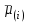 и
и  , то
, то  и так далее.
и так далее.
В пакете STATISTICA используется модифицированный вариант критерия Ньюмана-Келса, в котором в качестве статистики критерия используется величина
 .
.
Аналогичная статистика используется и в критерии Дункана, но в качестве критических точек берутся точки D-распределения Дункана c и
и  степенями свободы, где
степенями свободы, где  - число средних расположенных между
- число средних расположенных между  и
и 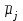 в вариационном ряду выборочных средних, включая
в вариационном ряду выборочных средних, включая  и
и 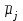 .
.
Методы множественного сравнения средних можно использовать не только для проверки гипотез о попарном различии средних, а также для проверки гипотез о различии средних для любых выбранных наборов групп. В силу этого, основная гипотеза в данных методах в общем случае имеет вид:
 ,
,
где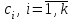 некоторые заданные константы, удовлетворяющие условию
некоторые заданные константы, удовлетворяющие условию  .
.
Например, при
, ,
,
мы будем проверять гипотезу или
или  .
.
При ,
,  ,
,
будем проверять гипотезу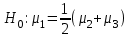 , то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д.
, то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д.
Линейные комбинации вида: ,
,  , то есть величины, пропорциональные разности между средними от средних, называются контрастами.
, то есть величины, пропорциональные разности между средними от средних, называются контрастами.
Критерии LSD, Шеффе, HSD Тьюки легко модифицировать под проверку гипотезы . Например, статистика LSD критерия для проверки гипотезы
. Например, статистика LSD критерия для проверки гипотезы  будет иметь вид:
будет иметь вид:
 .
.
Критическими точками статистики, по прежнему, будут являться квантили распределения Стьюдента уровня с числом степеней свободы
с числом степеней свободы  .
.
Пример 1. Результаты ответов 400 респондентов на вопросы анкеты «Томск 400» «Есть ли у вас хронические заболевания: 1) сердечно-сосудистые; 2) бронхо-легочные; 3) желудочно-кишечного тракта; 4) эндокринологические; 5) опорно-двигательной системы; 6) невралгические (в том числе слух, зрение); 7) урологические (гинекологические)» с вариантами ответов: “Да”, “Нет” оформлены в виде 7 числовых выборок кодов ответов с названиями «ЗБ1» - «ЗБ7». Код ответа соответствует номеру ответа. Также имеется выборка «НП» числовых кодов, соответствующих месту проживания респондента (1 – «Томск», 2 - «Северск», 3 – «Томский район», 4 - «Асино», 5 – «Асиновский район», 6 - «Каргасокский район», 7 – «Каргасок», 8 - «Тегульдет»). Используя дисперсионный анализ, установить, одинаков ли уровень различных заболеваний в различных населенных пунктах.
Используя имеющиеся данные, можно сформулировать различные задачи дисперсионного анализа в рамках анализа уровня заболеваний в различных населенных пунктах. Можно проверить гипотезу о различии уровня заболеваний (по всем заболеваниям) по населенным пунктам – это будет в данном случае задача многомерного однофакторного дисперсионного анализа. Можно проверить гипотезы о различии уровней заболеваний по каждому заболеванию в отдельности по различным населенным пунктам. В этом случае мы получим совокупность задач, каждая из которых относится к одномерному однофакторному дисперсионному анализу.
Поскольку мы имеем дело с дихотомическими данными, анализ различий в данном случае равносилен проверке гипотез о различии частот заболеваний. Чтобы воспользоваться параметрическим аппаратом статистики, необходимо чтобы коды ответов содержали значения “1” и “0”. В этом случае среднее арифметическое значение признака будет являться его относительной частотой, и задача сравнения частот сводится к задаче сравнения средних, для которой можно использовать параметрические методы. Поскольку в нашем случае коды ответов иные, необходимо перекодировать данные, либо вручную, либо так, как это сделано в примере 6. В результате ответам “Да”, “Нет” у нас буду соответствовать коды «1» и «0».
Рассмотрим самую простую реализацию однофакторного дисперсионного анализа в пакете статистика, используя соответствующий модуль в меню «Basic Statisics/Tables». Запускаем в головном меню модуль «Statistics», в стартовой панели выбираем пункт «Basic Statisics/Tables».
 , где
, где 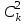 - число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из
- число сравнений. Данная величина гарантирует, что вероятность отклонение нулевой гипотезы (при ее истинности) хотя бы в одном из 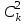 сравнений не превзойдет
сравнений не превзойдет  . Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия.
. Однако, принцип Бонферрони является чересчур консервативным, он приводит к существенному снижению мощности критерия.LSD – критерий и критерий Бонферрони занимают как бы самые крайние позиции в ряду критериев множественных сравнений. Среди остальных критериев множественного сравнения средних можно выделить критерии множественных сравнений Шеффе, Ньюмена-Келса, Тьюки и другие.
В методе множественных сравнений Шеффе для проверки гипотезы равенства средних
 и
и  используется статистика:
используется статистика: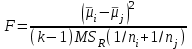 ,
,где
 – оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики
– оценка внутригрупповой (остаточной) дисперсии, полученная в ходе дисперсионного анализа. Если наблюдаемое значение статистики  , где
, где  - критическая точка распределения Фишера уровня
- критическая точка распределения Фишера уровня  (или квантиль уровня
(или квантиль уровня  ) с числом степеней свободы
) с числом степеней свободы  и
и  , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза  .
. Заметим, что в отличии от LSD критерия, где статистика
 имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет
имеет одну степень свободы, в критерии Шеффе предполагается, что статистика имеет
 степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана.
степень свободы. Критерий Шеффе также относится к достаточно консервативным критериям, то есть обладает малой мощностью. Более мощными, соответственно, более чувствительными являются критерии Тьюки, Ньюмена-Келса, Дункана.В методе множественных сравнений Тьюки (или достоверно значимой разности – HSD) для проверки гипотезы
 против альтернативы
против альтернативы  используется статистика:
используется статистика: ,
,значения которой сравниваются с критическими точками уровня
 распределения стьюдентизированного размаха с
распределения стьюдентизированного размаха с 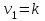 и
и  степенями свободы. Если наблюдаемое значение статистики
степенями свободы. Если наблюдаемое значение статистики  , где
, где 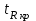 - критическая точка распределения стьюдентизированного размаха уровня
- критическая точка распределения стьюдентизированного размаха уровня  (или квантиль уровня
(или квантиль уровня  ) с числом степеней свободы
) с числом степеней свободы 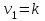 и
и  , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза  .
. Если объемы выборок различаются сильно, то рекомендуется использовать HSD критерий Тьюки для неравных выборок (критерий Spjovoll-Stoline). Статистика критерия в этом случае имеет вид:
 .
.Критические точки определяются также, как и для критерия HSD Тьюки.
В критерии Ньюмана-Келса используется та же статистика, что и в критерии Тьюки, однако по другому определяются критические точки. В качестве критических точек критерия Ньюмана-Келса используются критические точки распределения стьюдентизированного размаха с
 и
и  степенями свободы, где
степенями свободы, где 
- число средних расположенных между
 и
и 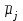 в вариационном ряду выборочных средних, включая
в вариационном ряду выборочных средних, включая  и
и 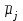 . Например, если сравниваются значения
. Например, если сравниваются значения 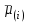 и
и 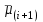 вариационного (упорядоченного) ряда средних, то
вариационного (упорядоченного) ряда средних, то  , если сравниваются значения
, если сравниваются значения 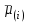 и
и  , то
, то  и так далее.
и так далее.В пакете STATISTICA используется модифицированный вариант критерия Ньюмана-Келса, в котором в качестве статистики критерия используется величина
 .
.Аналогичная статистика используется и в критерии Дункана, но в качестве критических точек берутся точки D-распределения Дункана c
 и
и  степенями свободы, где
степенями свободы, где  - число средних расположенных между
- число средних расположенных между  и
и 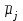 в вариационном ряду выборочных средних, включая
в вариационном ряду выборочных средних, включая  и
и 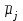 .
.Методы множественного сравнения средних можно использовать не только для проверки гипотез о попарном различии средних, а также для проверки гипотез о различии средних для любых выбранных наборов групп. В силу этого, основная гипотеза в данных методах в общем случае имеет вид:
 ,
,где
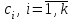 некоторые заданные константы, удовлетворяющие условию
некоторые заданные константы, удовлетворяющие условию  .
.Например, при

,
 ,
,мы будем проверять гипотезу
 или
или  .
.При
 ,
,  ,
,будем проверять гипотезу
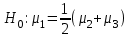 , то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д.
, то есть, гипотезу однородности первой и совокупности второй и третьей групп и т.д.Линейные комбинации вида:
 ,
,  , то есть величины, пропорциональные разности между средними от средних, называются контрастами.
, то есть величины, пропорциональные разности между средними от средних, называются контрастами.Критерии LSD, Шеффе, HSD Тьюки легко модифицировать под проверку гипотезы
 . Например, статистика LSD критерия для проверки гипотезы
. Например, статистика LSD критерия для проверки гипотезы  будет иметь вид:
будет иметь вид: .
.Критическими точками статистики, по прежнему, будут являться квантили распределения Стьюдента уровня
 с числом степеней свободы
с числом степеней свободы  .
.4. Дисперсионный анализ социологических признаков в пакете STATISTICA.
Пример 1. Результаты ответов 400 респондентов на вопросы анкеты «Томск 400» «Есть ли у вас хронические заболевания: 1) сердечно-сосудистые; 2) бронхо-легочные; 3) желудочно-кишечного тракта; 4) эндокринологические; 5) опорно-двигательной системы; 6) невралгические (в том числе слух, зрение); 7) урологические (гинекологические)» с вариантами ответов: “Да”, “Нет” оформлены в виде 7 числовых выборок кодов ответов с названиями «ЗБ1» - «ЗБ7». Код ответа соответствует номеру ответа. Также имеется выборка «НП» числовых кодов, соответствующих месту проживания респондента (1 – «Томск», 2 - «Северск», 3 – «Томский район», 4 - «Асино», 5 – «Асиновский район», 6 - «Каргасокский район», 7 – «Каргасок», 8 - «Тегульдет»). Используя дисперсионный анализ, установить, одинаков ли уровень различных заболеваний в различных населенных пунктах.
Используя имеющиеся данные, можно сформулировать различные задачи дисперсионного анализа в рамках анализа уровня заболеваний в различных населенных пунктах. Можно проверить гипотезу о различии уровня заболеваний (по всем заболеваниям) по населенным пунктам – это будет в данном случае задача многомерного однофакторного дисперсионного анализа. Можно проверить гипотезы о различии уровней заболеваний по каждому заболеванию в отдельности по различным населенным пунктам. В этом случае мы получим совокупность задач, каждая из которых относится к одномерному однофакторному дисперсионному анализу.
Поскольку мы имеем дело с дихотомическими данными, анализ различий в данном случае равносилен проверке гипотез о различии частот заболеваний. Чтобы воспользоваться параметрическим аппаратом статистики, необходимо чтобы коды ответов содержали значения “1” и “0”. В этом случае среднее арифметическое значение признака будет являться его относительной частотой, и задача сравнения частот сводится к задаче сравнения средних, для которой можно использовать параметрические методы. Поскольку в нашем случае коды ответов иные, необходимо перекодировать данные, либо вручную, либо так, как это сделано в примере 6. В результате ответам “Да”, “Нет” у нас буду соответствовать коды «1» и «0».
Рассмотрим самую простую реализацию однофакторного дисперсионного анализа в пакете статистика, используя соответствующий модуль в меню «Basic Statisics/Tables». Запускаем в головном меню модуль «Statistics», в стартовой панели выбираем пункт «Basic Statisics/Tables».

