ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 58
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Многофакторный дисперсионный анализ
Если анализируется одновременное влияние двух и более различных факторов на результаты наблюдений, то используется многофакторный дисперсионный анализ. Например, двухфакторная модель нам потребуется, если мы будем строить модель объяснения различий в средних доходов респондентов не только с учетом места проживания респондента, но и с учетом пола респондента.
Пусть мы исследуем влияние на величину
 двух факторов A и B, имеющих, соответственно
двух факторов A и B, имеющих, соответственно  и
и 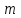 уровней. В двухфакторной модели дисперсионного анализа обычно исходят из следующей модели порождения данных:
уровней. В двухфакторной модели дисперсионного анализа обычно исходят из следующей модели порождения данных: ,
,где:
 - l-ое наблюдаемое значение отклика для i-го уровня фактора A и j-го уровня фактора B;
- l-ое наблюдаемое значение отклика для i-го уровня фактора A и j-го уровня фактора B; - среднее значение отклика по всей совокупности (генеральное среднее);
- среднее значение отклика по всей совокупности (генеральное среднее);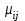 - среднее значение отклика для i-го уровня фактора A и j-го уровня фактора B;
- среднее значение отклика для i-го уровня фактора A и j-го уровня фактора B; - главный эффект i-го уровня фактора A (
- главный эффект i-го уровня фактора A (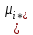 - среднее значение отклика для i-го уровня фактора A);
- среднее значение отклика для i-го уровня фактора A); - главный эффект j-го уровня фактора B (
- главный эффект j-го уровня фактора B ( - среднее значение отклика для j-го уровня фактора B);
- среднее значение отклика для j-го уровня фактора B); - эффект взаимодействия i-го уровня фактора A и j-го уровня фактора B;
- эффект взаимодействия i-го уровня фактора A и j-го уровня фактора B; - независимые случайные величины с математическим ожиданием равным нулю и одинаковой дисперсией
- независимые случайные величины с математическим ожиданием равным нулю и одинаковой дисперсией  .
.Заметим, что эффекты
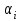 ,
,  ,
, 
удовлетворяют условиям:
 ,
,  ,
, 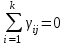 ,
, 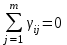 .
. Выражение
 можно представить в виде:
можно представить в виде: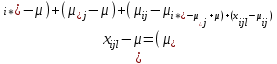 .
.Данное соотношение говорит о том, что отклонение наблюдаемого значения отклика складывается из суммы четырех слагаемых: отклонения отклика от среднего значения для i, j-го набора уровней факторов A и B
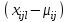 , главных эффектов i-го уровня фактора A и j-го уровня фактора B и эффекта взаимодействия. Что, означает, с учетом указанных выше условий на эффекты, что дисперсия отклика может быть представлена в виде суммы четырех дисперсий, одна из которых характеризует внутригрупповую изменчивость для i, j-го набора уровней факторов A и B, а остальные соответствующие эффекты.
, главных эффектов i-го уровня фактора A и j-го уровня фактора B и эффекта взаимодействия. Что, означает, с учетом указанных выше условий на эффекты, что дисперсия отклика может быть представлена в виде суммы четырех дисперсий, одна из которых характеризует внутригрупповую изменчивость для i, j-го набора уровней факторов A и B, а остальные соответствующие эффекты.Разложение общей дисперсии на составляющие для выборочных данных обычно записывается в виде равенства сумм квадратов соответствующих отклонений (которое, вообще говоря, справедливо только в случае выполнения условия пропорциональности
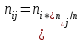 ):
): ,
,где:
 – общая, или полная, сумма квадратов отклонений;
– общая, или полная, сумма квадратов отклонений;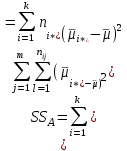 – сумма квадратов отклонений средних по уровням фактора A от общей средней, или сумма квадратов главных эффектов A;
– сумма квадратов отклонений средних по уровням фактора A от общей средней, или сумма квадратов главных эффектов A;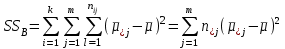 – сумма квадратов отклонений средних по уровням фактора B от общей средней, или сумма квадратов главных эффектов B;
– сумма квадратов отклонений средних по уровням фактора B от общей средней, или сумма квадратов главных эффектов B;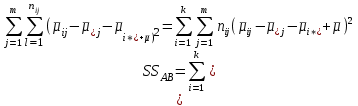 – сумма квадратов взаимодействия эффектов A и B;
– сумма квадратов взаимодействия эффектов A и B; – остаточная сумма квадратов отклонений.
– остаточная сумма квадратов отклонений.Число степеней свободы сумм квадратов
 и
и 
равно соответственно
 и
и 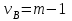 .
.Число степеней свободы сумм квадратов взаимодействия эффектов
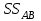 равно
равно  .
.Число степеней свободы сумм квадратов остатков
 равно
равно  .
.Соответственно средние суммы квадратов будут равны:
 ,
,  ,
,  ,
, 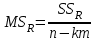 .
.Поскольку двухфакторная модель учитывает различные эффекты влияния факторов, то и статистический анализ для двухфакторной модели предполагает проверку гипотез о значимости различных эффектов. В качестве статистик критериев проверки гипотез о значимости соответствующих эффектов используются отношения средней суммы квадратов эффектов к средней сумме квадратов остатков. При условии истинности
 «эффект незначим» и нормальном распределении остатков данные статистики имеют распределение Фишера с параметрами степеней свободы, определяемыми числами степеней свободы соответствующих сумм, участвующих в отношении. В табл. 1 приведены основные рассматриваемые гипотезы, статистики критериев для проверки данных гипотез и соответствующие числа степеней свободы данных статистик.
«эффект незначим» и нормальном распределении остатков данные статистики имеют распределение Фишера с параметрами степеней свободы, определяемыми числами степеней свободы соответствующих сумм, участвующих в отношении. В табл. 1 приведены основные рассматриваемые гипотезы, статистики критериев для проверки данных гипотез и соответствующие числа степеней свободы данных статистик. Табл. 1. Статистики для проверки гипотез двухфакторного дисперсионного анализа
| Основная гипотеза: | Все  | Все  | Все 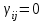 |
| Статистика критерия |  | 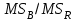 |  |
| Числа степеней свободы |   |   |   |
Если наблюдаемое значение статистики
 , где
, где  - критическая точка распределения Фишера уровня
- критическая точка распределения Фишера уровня  (или квантиль уровня
(или квантиль уровня  ) с числом степеней свободы
) с числом степеней свободы 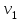 и
и  , то нулевая гипотеза отклоняется и считается, что средние для различных уровней фактора значимо различаются.
, то нулевая гипотеза отклоняется и считается, что средние для различных уровней фактора значимо различаются.3. Апостериорные множественные сравнения средних
Результат дисперсионного анализа, указывающий, что средние значения отклика для разных уровней фактора, различаются, не является окончательным результатом анализа изучаемого явления. Это скорее промежуточный результат, который подразумевает дальнейшее раскрытие того, для каких уровней фактора средние больше, для каких меньше, а для каких одинаковы. Основная процедура дисперсионного анализа не дает возможности ответить на эти вопросы.
Самый очевидный и простой вариант решения данной задачи - провести серию по парных сравнений при помощи t-критерия, используя в качестве оценки дисперсии величину
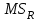 - оценку внутригрупповой дисперсии, полученную в ходе дисперсионного анализа. Такой подход реализуется в так называемом методе наименьшей значимой разности (LSD). Статистика критерия LSD для проверки гипотезы равенства средних
- оценку внутригрупповой дисперсии, полученную в ходе дисперсионного анализа. Такой подход реализуется в так называемом методе наименьшей значимой разности (LSD). Статистика критерия LSD для проверки гипотезы равенства средних 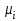 и
и  имеет вид:
имеет вид: .
.Если наблюдаемое значение статистики
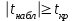 , где
, где  - критическая точка распределения Стьюдента уровня
- критическая точка распределения Стьюдента уровня 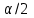 (или квантиль уровня
(или квантиль уровня 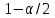 ) с числом степеней свободы
) с числом степеней свободы  , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза  .
.Однако, такой подход является не совсем корректным. Если задать, скажем, 5% уровень значимости, то при каждом сравнении вероятность отклонить нулевую гипотезу будет равна 5%, а при серии по парных сравнений вероятность отклонить хотя бы одну нулевую гипотезу в таком случае существенно превысит 5%. Например, при по парном сравнении средних 4 групп, эта вероятность составит 26,5 %.
Существуют разные подходы к решению данной проблемы. Один из них – уменьшить уровень значимости при по парном сравнении так, чтобы вероятность хотя бы одного отклонения нулевой гипотезы равнялось заданному уровню значимости. Такой подход реализуется в

